Python求解线性规划——PuLP使用教程

简洁是智慧的灵魂，冗长是肤浅的藻饰。——莎士比亚《哈姆雷特》

1 PuLP 库的安装

如果您使用的是 Anaconda^[1] 的话（事实上我也更推荐这样做），需要先激活你想要安装的虚拟环境，之后在 Prompt 输入

pip install pulp

不出意外的话等一会就安装完毕。

2 线性规划简介

想必大家能点开这篇文章一定都知道线性规划是什么意思吧……那么我用两个例子再简单说一下。

2.1 线性规划

2.1.1 题目描述^[2]

若变量 \(x, y\) 满足约束条件：

\[\left\{
\begin{aligned}
& 2x + 3y - 6\geq 0\\
& x + y - 3 \leq 0\\
& y - 2 \leq 0
\end{aligned}
\right.
\]

求 \(z = 3x + y\) 的最大值。

2.1.2 基本概念

首先，我们要认清在这道题中，\(x\) 和 \(y\) 是可以变的，所以把它们叫做决策变量。三个不等式叫做约束条件，即 \(x\) 和 \(y\) 必须同时满足这三个不等式。我们若画出图来：

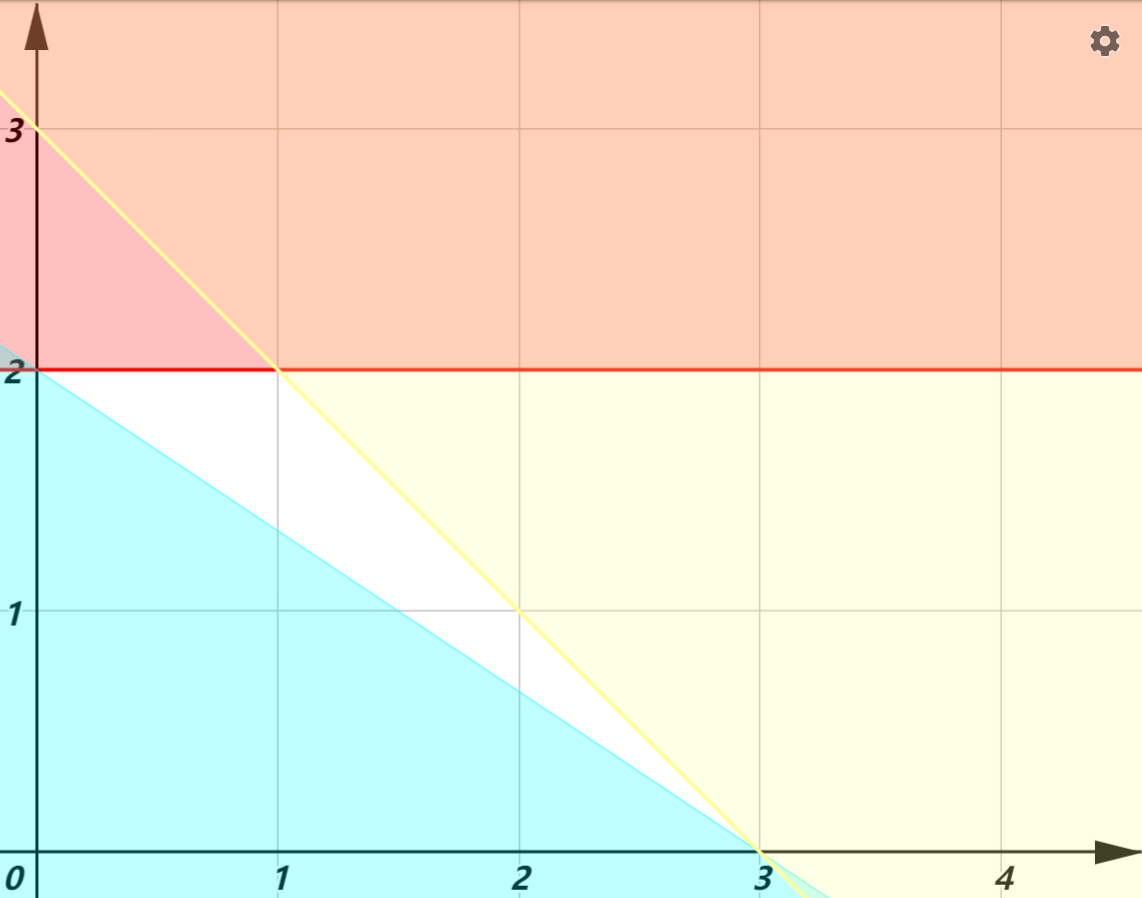
其中不满足约束条件的区域被我标上了颜色，所以 \(x, y\) 可以取得值只能在纯白区域内，这一片区域称作可行域。

再看最后的我们的目标：求 \(z = x + 3y\) 的最大值。

于是 \(z=x+3y\) 就被称作目标函数，我们的工作就是求这个目标函数的最大值。

整个问题描述为：

\[\begin{eqnarray*}
&\max &z = x+3y \tag{1}\\
&\mathrm{s.t.} & \quad 2x + 3y - 6 \geq0 \tag{2}\\
& & \quad x + 3y - 3 \leq 0 \tag{3}\\
& & \quad y - 2 \leq 0 \tag{4}
\end{eqnarray*}
\]

然后怎么算？别急我们再看一个例子。

2.2 整数规划

2.2.1 题目描述^[3]

汽车厂生产小、中、大三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求以及利润如下表所示。要求每月的钢材消耗不超过 600 t，总劳动时间不超过 60 000 h。试指定生产计划使得工厂每月的利润最大。

	小型车	中型车	大型车
钢材 / t	1.5	3	5
劳动时间 / h	280	250	400
利润 / 万元	2	3	4

2.2.2 解题思路

首先，设三个决策变量，用 \(x_1, x_2, x_3\) 分别表示生产小型车、中型车、大型车的数量，但是注意要满足：

• 车的数量只能是整数；
• 车的数量大于等于 0。

其他约束条件看题直接列：

\[\left\{\begin{aligned}
& 1.5 x_1 + 3 x_2 + 5 x_3 \leq 600\\
& 280 x_1 + 250 x_2 + 400 x_2 \leq 60000
\end{aligned}\right.
\]

最后写出目标函数：

\[z = 2x_1 + 3x_2 + 4x_3
\]

综合起来整个问题描述为：

\[\begin{eqnarray*}
&\max & z = 2x_1 + 3x_2 + 4x_3 \tag{1}\\
&\mathrm{s.t.} & 1.5 x_1 + 3 x_2 + 5 x_3 \leq 600\tag{2}\\
& & 280 x_1 + 250 x_2 + 400 x_2 \leq 60000\tag{3}\\
& & x_1, x_2, x_3 \geq 0\tag{4}\\
& & x_1, x_2, x_3 均为整数\tag{5}
\end{eqnarray*}
\]

另外可以看出这个题由于涉及到三个决策变量，可行域是相当抽象的，这里就不画了 hhh~

3 求解过程

首先在最前面引入所需的pulp工具库：

import pulp as pl

这句话是引入 pulp 库并简写为 pl，一个 python 库只有在开始 import 了之后才能在后面使用。这样后面凡是用到 pulp 的功能都要写成 pl.xxx。

接下来是以下几个步骤：

• 定义模型
• 定义决策变量
• 添加约束条件
• 添加目标函数
• 模型求解
• 打印结果

3.1 定义模型

# Define the model
model = pl.LpProblem(name="My-Model", sense=pl.LpMaximize)

这个操作是使用 pl.LpProblem 创建了一个模型并赋值给变量 model，接收两个参数：

• name：模型的名字，随便起一个；
• sense：模型的类型，pl.LpMinimize是求目标函数的最小值，pl.LpMaximize 是求最大值

3.2 定义决策变量

# Define the decision variables
x = pl.LpVariable(name='x')
y = pl.LpVariable(name='y')

如果你的变量比较少的话可以简单这么写。这个意思是定义了两个浮点数变量，取值范围是整个实数域。注意等号左边的变量才是你在之后的计算式中使用的符号，而参数 name 只有在最后打印结果的时候才会被打印出来。另外如果你对变量有其他要求的话可以添加以下参数：

• lowBound：变量的最小取值（不写的话默认负无穷）；
• upBound：变量的最大取值（默认正无穷）；
• cat：变量的类型，有 pl.Binary 逻辑变量、pl.Integer 整数、pl.Continuous 实数（默认值）；

如果你的变量比较多而不得不用 1, 2, 3…… 来编号，可以采用类似这样的写法：

# Define the decision variables
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 9)}

这是一次定义 8 个变量并保存在一个类似数组的结构中，变量都是正整数，分别用 x[1], x[2], ..., x[8] 表示，依次命名为 x1, x2,..., x8。

注意 range(left, right) 表示的区间是左闭右开。

3.3 添加约束条件

# Add constraints
model += (2 * x + 3 * y - 6 >= 0, "constrain_1")
model += (x + 3 * y - 3 == 0, "constrain_2")

没错！如你所见就是这么简单，括号里第一个变量就是你的约束不等式或等式，第二个变量是你的自定义的约束名（可以起一个有意义的名字，当然也可以省略）。

由于一些比较数学的原因，约束条件里是不能使用大于号“>”或小于号“<”的。

如果你像前面一样把变量定义在了数组中，那么可以直接用方括号调用：

model += (2 * x[1] + 3 * x[2] - 6 >= 0)

3.4 添加目标函数

# Set the objective
model += x + 3 * y

与前面添加约束条件不同，添加目标函数这一步不用加最外层的括号。

3.5 模型求解

# Solve the optimization problem
status = model.solve()

就写这一句话，调用 model 的 solve() 方法，并把结果保存在 status 中。

3.4 打印结果

# Get the results
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")

for var in model.variables():
    print(f"{var.name}: {var.value()}")

for name, constraint in model.constraints.items():
    print(f"{name}: {constraint.value()}")

然后你就能看到模型求解的结果了。

4 示例代码

4.1 高考题代码

首先解决一下 3.1 的高考题：

import pulp as pl

# 定义一个模型，命名为 "Model_3.1"，求最大值
model = pl.LpProblem(name="Model_3.1", sense=pl.LpMaximize)

# 定义两个决策变量，取值为整个实数域
x = pl.LpVariable(name='x')
y = pl.LpVariable(name='y')

# 添加三个约束条件
model += (2 * x + 3 * y - 6 >= 0)
model += (x + y - 3 <= 0)
model += (y - 2 <= 0)

# 目标函数
model += x + 3 * y

# 求解
status = model.solve()

# 打印结果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")

for var in model.variables():
    print(f"{var.name}: {var.value()}")

for name, constraint in model.constraints.items():
    print(f"{name}: {constraint.value()}")

查看结果的最后几行：

status: 1, Optimal
objective: 7.0
x: 1.0
y: 2.0
_C1: 2.0
_C2: 0.0
_C3: 0.0

最大值是 \(7.0\)，在 \(x=1.0, y=2.0\) 时取到。

4.2 汽车厂代码

import pulp as pl

# 定义一个模型，命名为 "Model_3.2"，求最大值
model = pl.LpProblem(name="Model_3.2", sense=pl.LpMaximize)

# 定义三个决策变量，取值正整数
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 4)}

# 添加约束条件
model += (1.5 * x[1] + 3 * x[2] + 5 * x[3] <= 600)
model += (280 * x[1] + 250 * x[2] + 400 * x[3] <= 60000)

# 目标函数
model += 2 * x[1] + 3 * x[2] + 4 * x[3]

# 求解
status = model.solve()

# 打印结果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")

for var in model.variables():
    print(f"{var.name}: {var.value()}")

for name, constraint in model.constraints.items():
    print(f"{name}: {constraint.value()}")

查看结果的最后几行：

status: 1, Optimal
objective: 632.0
x1: 64.0
x2: 168.0
x3: 0.0
_C1: 0.0
_C2: -80.0

三种车的产量分别取 64、168、0，最大收益 632 万元。

---

1. 众所周知 Python 在各个领域如此受欢迎很大程度上是因为其有众多强大的第三方库，但是用的多了就会发现如果安装太多库就有点乱。而 Anaconda 就是一种很方便的管理 Python 环境的工具，不仅可以将不同的库分门别类管理好，更有用的是可以在电脑上安装不同版本的 Python 而不用担心会互相冲突。 ︎

2. 2019 年高考全数学国二卷。 ︎

3. 改编自姜启元等《数学模型（第五版）》108 页例 1。 ︎