Codeforces Round #817 (Div. 4)

CF传送门

因为洛谷题库未更新，所以给出的题面都是CF的。

现场打真是太卡了（梯子挂了，codeforc.es也崩了），所以五六分钟才打开题目 \(qwq\)

A. Spell Check

萌萌题，把字符串放桶里，判名字每个字母是否恰好出现一次即可。

\(9min\) \(AC\) \(qwq\) 都怪CF

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
string s;
int t[150],T,n;
void solve(){
	scanf("%d",&n);
	cin>>s;
	memset(t,0,sizeof(t));
	for(int i=0;i<n;i++) t[s[i]]++;
	if(t['T']==1&&t['i']==1&&t['m']==1&&t['u']==1&&t['r']==1&&n==5) printf("YES\n");
	else printf("NO\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

---

B. Colourblindness

萌萌题\(\times 2\)，将 \(G\) 和 \(B\) 视为相同，然后比一下两个字符串即可。

\(15min\) \(AC\)

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
string s1,s2;
int T,n;
bool a[105],b[105];
void solve(){
	scanf("%d",&n);
	cin>>s1>>s2;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	for(int i=0;i<n;i++){
		if(s1[i]=='R') a[i]=1;
		if(s2[i]=='R') b[i]=1;
	}
	for(int i=0;i<n;i++){
		if(a[i]!=b[i]){
			printf("NO\n");
			return ;
		}
	}
	printf("YES\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

---

C. Word Game

用三个 \(map\) 表示三个人每次用到过的字符串，然后分别判断其他两人有没有用过，并计算答案即可。

\(25min\) \(AC\)

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T,n;
string s1[1005],s2[1005],s3[1005];
int ans1,ans2,ans3;
void solve(){
	scanf("%d",&n);
	map<string,bool> a,b,c;
	ans1=ans2=ans3=0;
	for(int i=1;i<=n;i++) cin>>s1[i],a[s1[i]]=1;
	for(int i=1;i<=n;i++) cin>>s2[i],b[s2[i]]=1;
	for(int i=1;i<=n;i++) cin>>s3[i],c[s3[i]]=1;
	for(int i=1;i<=n;i++){
		if(b[s1[i]]+c[s1[i]]==0) ans1+=3;
		else if(b[s1[i]]+c[s1[i]]==1) ans1+=1;
	}
	for(int i=1;i<=n;i++){
		if(a[s2[i]]+c[s2[i]]==0) ans2+=3;
		else if(a[s2[i]]+c[s2[i]]==1) ans2+=1;
	}
	for(int i=1;i<=n;i++){
		if(b[s3[i]]+a[s3[i]]==0) ans3+=3;
		else if(b[s3[i]]+a[s3[i]]==1) ans3+=1;
	}
	printf("%d %d %d\n",ans1,ans2,ans3);
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

---

D. Line

首先可以知道，左半边的 \(L\) 改为 \(R\) 可以使答案更优，右半边的 \(R\) 改为 \(L\) 可以使答案更优。

所以只要先算出初始的答案，然后 \(l,r\) 从两边往中间扫，发现可以改的就更新答案并输出，同时 \(cnt\) 记着更新了几次。最后 \(cnt\) 还不到 \(n\) 的话说明已经最优不用改了，输出 \(n-cnt\) 次最终答案即可。

几个不等号注意一下即可。

\(41min\) \(AC\) \(qwq\)

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T,n;
ll ans;
string s;
void solve(){
	scanf("%d",&n);
	cin>>s;
	ans=0;
	for(int i=0;i<n;i++){
		if(s[i]=='L') ans+=(ll)i;
		else ans+=(ll)n-(ll)i-1ll;
	}
	int cnt=0,now=0;
	for(int l=0,r=n-1;l<=n/2,r>=n/2;l++,r--){
		if(s[l]=='L'){
			now++;
			ans-=(ll)l;
			ans+=(ll)n-(ll)l-1ll;
		}
		if(now>cnt){
			cnt=now;
			printf("%lld ",ans);
		}
		if(s[r]=='R'){
			now++;
			ans+=(ll)r;
			ans-=(ll)n-(ll)r-1ll;
		}
		if(now>cnt){
			cnt=now;
			printf("%lld ",ans);
		}
	}
	for(int i=1;i<=n-cnt;i++) printf("%lld ",ans);
	printf("\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

---

E. Counting Rectangles

数据范围要求 \(O(1)\) 查询，所以一眼矩阵前缀和。

只需要预处理出 \(1000 \times 1000\) 范围内的 \(sum[i][j]\)，表示 \(i\times j\) 的矩形可以容纳的答案即可。

同时注意，可能有重复的边长（如样例最后一组），所以 \(sum\) 初始时要 \(+=\)

但是这个菜ji赛时输出的调挂了喜提 WA

Code:

#include<bits/stdc++.h>
#define ll long long
int T,n,q;
ll sum[1005][1005],x,y;
void solve(){
	memset(sum,0,sizeof sum);
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld",&x,&y);
		sum[x][y]+=x*y;
	}
	for(int i=1;i<=1000;i++){
		for(int j=1;j<=1000;j++) sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
	}
	for(int i=1;i<=q;i++){
		int u,v,w,z;
		scanf("%d%d%d%d",&u,&v,&w,&z);
		printf("%lld\n",sum[w-1][z-1]+sum[u][v]-sum[u][z-1]-sum[w-1][v]);
	}
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}

---

F. L-shapes

其实这题根本不用搜索，有耐心即可。

可以发现，在 \(n\times m\) 范围内扫，可能合法的只有以下四种情况，其中蓝色代表示是 *，红色表示不能是 *，其中黄色五角星表示当前 \(i,j\) 的位置。

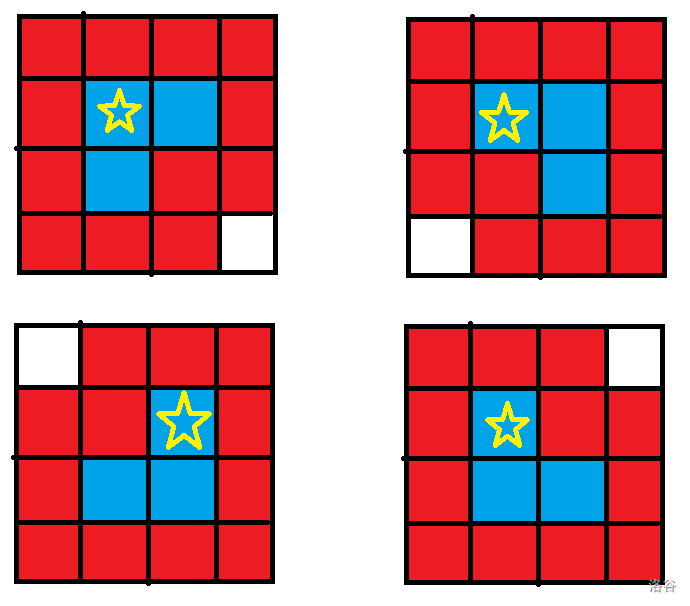
所以只要把 * 标记为 \(1\)，全图扫一遍，发现合法就给它变 \(0\)，看最后有没有 \(1\) 剩余即可。

因为 \(E\) 卡太久，\(1h\) \(45min\) 才 \(AC\) \(qwq\)

Code：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T,n,m,a[55][55];
char c;
void search(int i,int j){
	if(a[i+1][j]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-1]&&!a[i][j+1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+2]&&
	   !a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i+1][j]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i+1][j-1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-2]&&!a[i][j-1]&&!a[i][j+1]&&!a[i+1][j-2]&&!a[i+1][j+1]&&
	   !a[i+2][j-2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i+1][j-1]=a[i+1][j]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j]&&
	   !a[i+1][j+2]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i][j+1]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+1]&&
	   !a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i][j+1]=a[i+1][j]=0;
		return ;
	}
}
void solve(){
	scanf("%d%d",&n,&m);
	memset(a,0,sizeof(a));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='*') a[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1) search(i,j);
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1){
				printf("NO\n");
				return ;
			}
		}
	}
	printf("YES\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

---

G. Even-Odd XOR

巧妙的构造。赛时来不及了

应该有很多种方法，说一下我的想法。

首先发现从 \(0\) 开始排的有序数列，它的奇数位、偶数位的异或和很有特点（可以手算）。只要有办法让他们都等于 \(0\) 就是合法的答案了。

同时可以得知，要使 \(x_1\) 到 \(x_n\) 的异或和为 \(0\)，只需要 \(x_1\) 到 \(x_{n-1}\) 的异或和等于 \(x_n\) 即可。

所以计一个 \(k\) 表示 \(0\) 到 \(n-1\) 的异或和放在最后，但发现这样能会出现重复数字，比如 \(0\) 到 \(7\) 异或和为 \(0\)，数列出现两个 \(0\) 就不合法了。

所以想到搞两个大数，比如 \(x=2^{24}\) 和 \(y=2^{25}\)，各放在奇、偶位，同时将得到的 \(k\oplus x\oplus y\) ,答案就还是合法的且不会重复。多出两个数怎么办？\(0\) 到 \(n-1\) 改为到 \(n-3\) 即可。

Code：

#include <bits/stdc++.h>
using namespace std;
int T,n,k;
void solve(){
	scanf("%d",&n);
	k=0;
    for(int i=0;i<n-3;i++){
		printf("%d ",i);
		k^=i;
	}
	int x=1<<24,y=1<<25;
	printf("%d %d %d\n",k^x^y,x,y);
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}

G L & H F !