[leetcode] 994. Rotting Oranges

题目

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

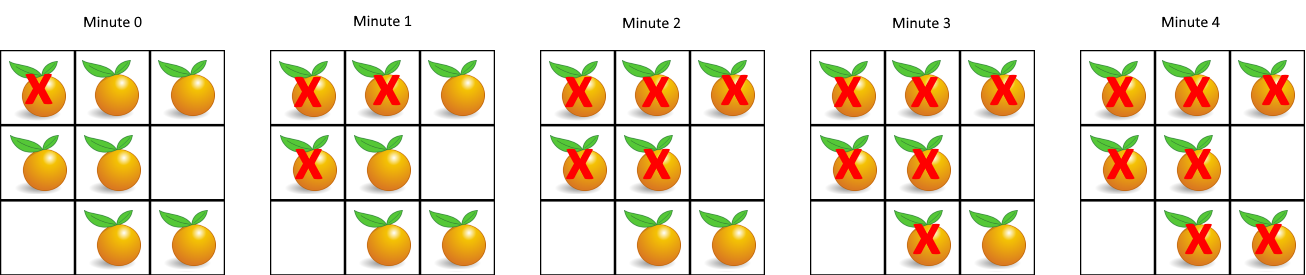
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

思路

bfs模拟橘子变质的过程。

代码

python版本：

from collections import deque

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        res = 0
        q = deque()
        [q.append((i, j, 0)) for i in range(len(grid)) for j in range(len(grid[0])) if grid[i][j] == 2]
        while len(q):
            i, j, count = q.popleft()
            if grid[i][j] == 2 and count:
                continue
            grid[i][j] = 2
            res = max(res, count)
            for l, r in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
                if 0 <= i+l < len(grid) and 0 <= j+r < len(grid[0]) and grid[i+l][j+r] == 1:
                    q.append((i+l, j+r, count+1))
        has = any([j == 1 for i in grid for j in i])
        return -1 if has else res