基于python的数学建模---非线性规划

• 凸函数的非线性规划

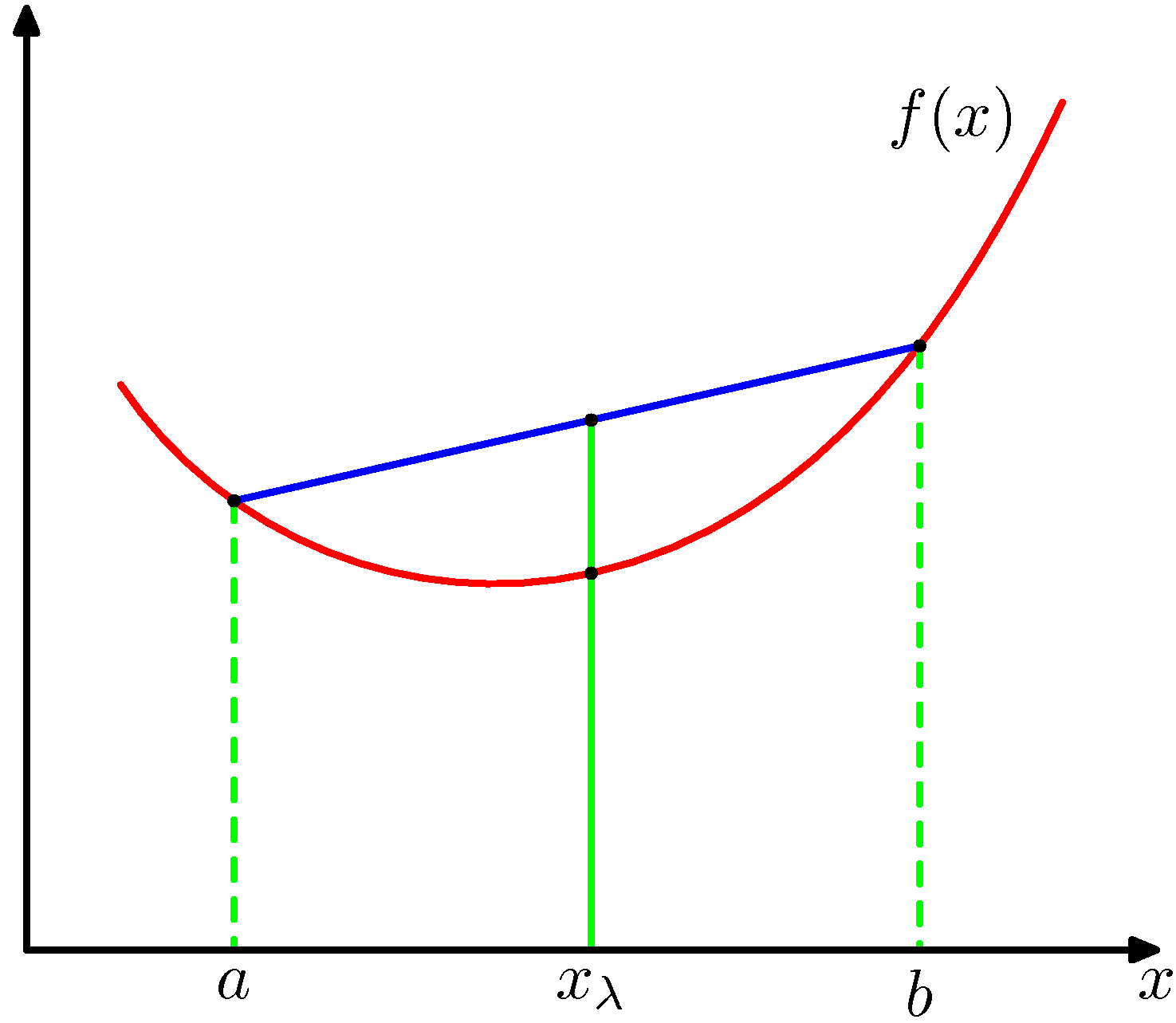
minimize 求解的是局部最优解

简单的函数，无所谓 复杂的函数 初始值的设定很重要

scipy.optimize.minimize(fun,x0,args=(),method=None,jac=None,hess=None,hessp=None,bounds= None,constaints=() , tol= None,Callback= None, options=None)

fun:求最小值的目标函数

args:常数值

constraints :约束条件

method:求极值方法，一 般默认。

xO:变量的初始猜测值，注意minimize是局部最优

• instance1

计算1/x + x 的最小值

from scipy.optimize import minimize
import numpy as np

def fun(args):
    a = args
    v = lambda x: a / x[0] + x[0]
    return v

if __name__ == '__main__':
    args = (1,)   #使用元组
    x0 = np.asanyarray((2,))
    res = minimize(fun(args), x0, method='SLSQP')
    print(res.fun)
    print(res.success)
    print(res.x)

2.0000000815356342
True
[1.00028559]

• instance2

计算(2+x1)/(1+x2)−3x1+4x3的最小值，其中x1、x2、x3范围在0.1 到 0.9 之间

from scipy.optimize import minimize
import numpy as np

def fun(args):
    a, b, c, d = args
    v = lambda x: (a + x[0]) / (b + x[1]) - c * x[0] + d * x[2]
    return v

def con(args):
    # 0.1 0.9 0.1 0.9
    x1min, x1max, x2min, x2max, x3min, x3max = args
    # eq 等式等于零  ineq 等式大于零
                                 # x1 - 0.1 > 0
    cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},
                                 # 0.9 - x1 > 0     这样就将x 限制在0.1 ~ 0.9 之中
            {'type': 'ineq', 'fun': lambda x: -x[0] + x1max},
            {'type': 'ineq', 'fun': lambda x: x[1] - x2min},
            {'type': 'ineq', 'fun': lambda x: -x[1] + x2max},
            {'type': 'ineq', 'fun': lambda x: x[2] - x3min},
            {'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
    return cons

if __name__ == '__main__':
    args = (2, 1, 3, 4,)
    args1 = (0.1, 0.9, 0.1, 0.9, 0.1, 0.9,)
    cons = con(args1)

    # 初始猜想值 要设的好
    x0 = np.asarray((0.5, 0.5, 0.5,))
    res = minimize(fun(args), x0, method='SLSQP', constraints=cons)
    print(res.fun)
    print(res.success)
    print(res.x)

-0.773684210526435
True
[0.9 0.9 0.1]