【acmm】一道简单的数学题

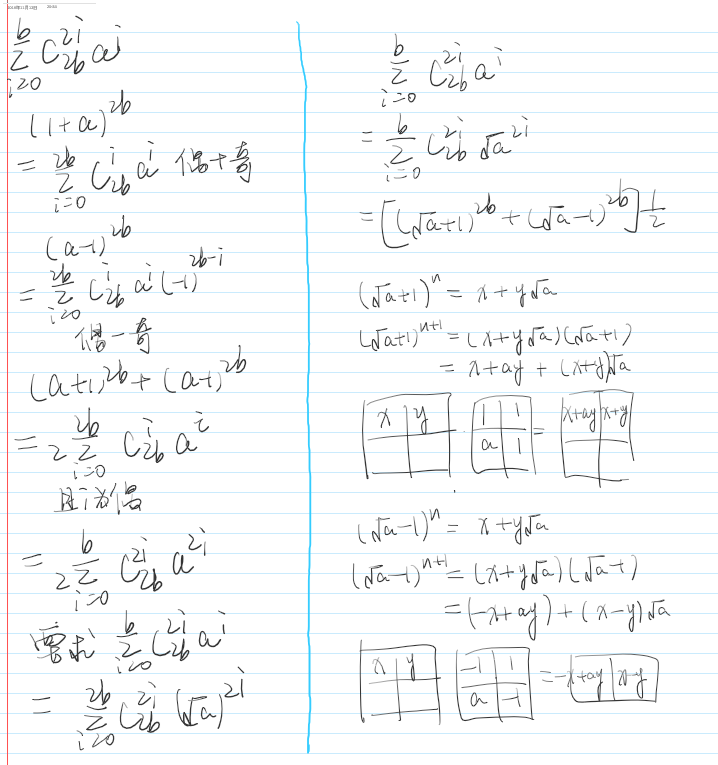
emm卡常

我本来写成了这个样子：

 #include<bits/stdc++.h>
 using namespace std;

 typedef long long LL;
 const LL mod = 1e9+;
 struct node{
     LL s[][];
 };
 LL m0[][]={,,,};
 LL m1[][]={-,,,-};

 node mult(node x,node y)
 {
     node ans;
     memset(ans.s,,sizeof(ans.s));
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             for(int k=;k<;k++)
                 ans.s[i][j]=(ans.s[i][j]+(x.s[i][k]*y.s[k][j])%mod)%mod;
     return ans;
 }

 node quickpow(node t,LL x)
 {
     node ans,now=t;
     memset(ans.s,,sizeof(ans.s));
     ans.s[][]=ans.s[][]=;
     while(x)
     {
         if(x&) ans=mult(ans,now);
         now=mult(now,now);x/=;
     }
     return ans;
 }

 int main()
 {
     //freopen("a.in","r",stdin);
     //freopen("b.out","w",stdout);
     int T;LL a,b;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lld%lld",&a,&b);
         m0[][]=a;m1[][]=a;
         node t0,t1;
         for(int i=;i<;i++)
             for(int j=;j<;j++)
             {
                 t0.s[i][j]=m0[i][j];
                 t1.s[i][j]=m1[i][j];
             }
         t0=quickpow(t0,*b-);
         t1=quickpow(t1,*b-);
         LL ans=;
         ans=(((t0.s[][]+t0.s[][])%mod+(-t1.s[][]+t1.s[][])%mod)/)%mod;
         printf("%lld\n",ans);
     }
     return ;
 }

后来把矩乘全部直接改掉才a了

 #include<bits/stdc++.h>
 using namespace std;

 typedef long long LL;
 const LL mod = 1e9+;
 LL a,b,ans[][],now[][],p[][];

 void quickpow(int tmp,LL x)
 {
     if(!tmp)
     {
         now[][]=,now[][]=;
         now[][]=a,now[][]=;
     }
     else
     {
         now[][]=-,now[][]=;
         now[][]=a,now[][]=-;
     }
     ans[][]=,ans[][]=;
     ans[][]=,ans[][]=;
     while(x)
     {
         if(x&)
         {
             for(int i=;i<;i++)
                 for(int j=;j<;j++)
                     p[i][j]=ans[i][j];
             ans[][]=(p[][]*now[][]+p[][]*now[][])%mod;
             ans[][]=(p[][]*now[][]+p[][]*now[][])%mod;
             ans[][]=(p[][]*now[][]+p[][]*now[][])%mod;
             ans[][]=(p[][]*now[][]+p[][]*now[][])%mod;
         }
         for(int i=;i<;i++)
             for(int j=;j<;j++)
                 p[i][j]=now[i][j];
         now[][]=(p[][]*p[][]+p[][]*p[][])%mod;
         now[][]=(p[][]*p[][]+p[][]*p[][])%mod;
         now[][]=(p[][]*p[][]+p[][]*p[][])%mod;
         now[][]=(p[][]*p[][]+p[][]*p[][])%mod;
         x/=;
     }
 }

 int main()
 {
     //freopen("a.in","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lld%lld",&a,&b);
         quickpow(,*b-);
         LL sum=(ans[][]+ans[][])%mod;
         quickpow(,*b-);
         sum=((sum+(-ans[][]+ans[][])%mod)/)%mod;
         printf("%lld\n",sum);
     }
     return ;
 }