应该也不是工具的问题吧，更多的是图片。但是不知道咋取就写工具了。

比如：http://ctf5.shiyanbar.com/stega/chromatophoria/steg.png

我在想为毛要选择

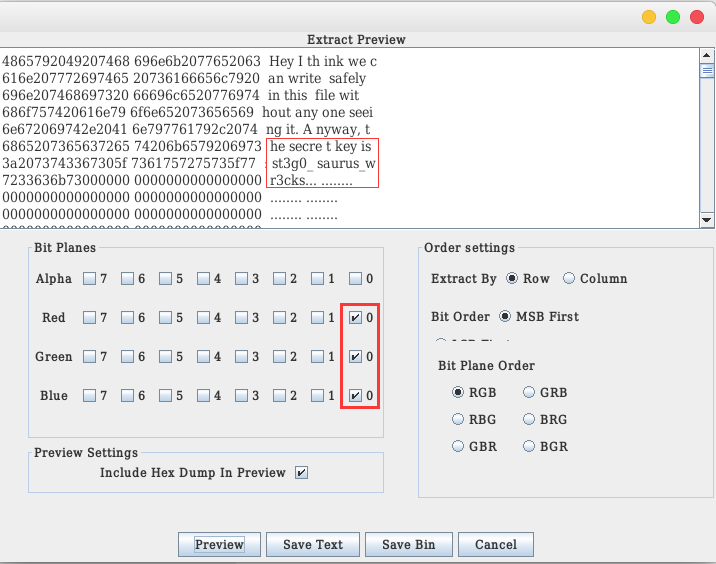
才能得到key

抱着这个想法就开始了今天的研究。

这是原图：

然后我点击向右。

发现Alpha plane 7一直到Alpha plane 0都是差不多的图片（空白的）

然后再向右，到了red发现7-1也都是差不多（图片有变化但还能看清图），但是到了0的时候差距就完全不一样了（纯黑）。

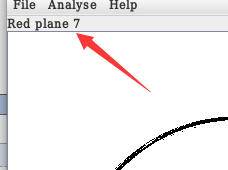
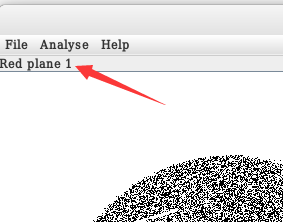
Green plance的也是7-1的时候都是差不多但是到了0的时候就完全黑了。

所以这就有了选择RGB的red、green和blue的最低位0的道理了。我之前还以为都TMD是瞎JB点。

stegsolve使用探究的更多相关文章

  1. stegsolve使用方法

    Stegsolve使用方法(是因为ctf题总是遇到并且目前百度没有十分详细的探究说明) 这个没什么好说的,打开文件 ,保存,退出 在分析里面从上到下的依次意思是 File Format:文件格式 Da ...

  2. stegsolve.jar压缩包打开和使用方法

    1.stegsolve.jar下载 下载地址:http://www.caesum.com/handbook/Stegsolve.jar 2.stegsolve.jar打开方法 (1)需要下载java并 ...

  3. 探究javascript对象和数组的异同，及函数变量缓存技巧

    javascript中最经典也最受非议的一句话就是:javascript中一切皆是对象.这篇重点要提到的,就是任何jser都不陌生的Object和Array. 有段时间曾经很诧异,到底两种数据类型用来 ...

  4. [原] KVM 虚拟化原理探究（1）— overview

    KVM 虚拟化原理探究- overview 标签(空格分隔): KVM 写在前面的话 本文不介绍kvm和qemu的基本安装操作,希望读者具有一定的KVM实践经验.同时希望借此系列博客,能够对KVM底层 ...

  5. [原] KVM 虚拟化原理探究 —— 目录

    KVM 虚拟化原理探究 -- 目录 标签(空格分隔): KVM KVM 虚拟化原理探究(1)- overview KVM 虚拟化原理探究(2)- QEMU启动过程 KVM 虚拟化原理探究(3)- CP ...

  6. [原] KVM 虚拟化原理探究（6）— 块设备IO虚拟化

    KVM 虚拟化原理探究(6)- 块设备IO虚拟化 标签(空格分隔): KVM [toc] 块设备IO虚拟化简介 上一篇文章讲到了网络IO虚拟化,作为另外一个重要的虚拟化资源,块设备IO的虚拟化也是同样 ...

  7. [原] KVM 虚拟化原理探究（5）— 网络IO虚拟化

    KVM 虚拟化原理探究(5)- 网络IO虚拟化 标签(空格分隔): KVM IO 虚拟化简介 前面的文章介绍了KVM的启动过程,CPU虚拟化,内存虚拟化原理.作为一个完整的风诺依曼计算机系统,必然有输 ...

  8. [原] KVM 虚拟化原理探究（4）— 内存虚拟化

    KVM 虚拟化原理探究(4)- 内存虚拟化 标签(空格分隔): KVM 内存虚拟化简介 前一章介绍了CPU虚拟化的内容,这一章介绍一下KVM的内存虚拟化原理.可以说内存是除了CPU外最重要的组件,Gu ...

  9. [原] KVM 虚拟化原理探究（3）— CPU 虚拟化

    KVM 虚拟化原理探究(3)- CPU 虚拟化 标签(空格分隔): KVM [TOC] CPU 虚拟化简介 上一篇文章笼统的介绍了一个虚拟机的诞生过程,从demo中也可以看到,运行一个虚拟机再也不需要 ...

随机推荐

  1. v-for & duplicate key bug

    v-for & duplicate key bug vue warn & v-for & duplicate key bug <span class="audi ...

  2. hdu 6434 Count (欧拉函数)

    题目链接 Problem Description Multiple query, for each n, you need to get $$$$$$ \sum_{i=1}^{n} \sum_{j=1 ...

  3. 最小生成树-Borůvka算法

    一般求最小生成树的时候,最流行的是Kruskal算法,一种基于拟阵证明的贪心,通过给边排序再扫描一次边集,利用并查集优化得到,复杂度为\(O(ElogE)\).另一种用得比较少的是Prim算法,利用优 ...

  4. 【刷题】洛谷 P4143 采集矿石

    题目背景 ZRQ成功从坍塌的洞穴中逃了出来.终于,他看到了要研究的矿石.他想挑一些带回去完成任务. 题目来源:Zhang_RQ哦对了ZRQ就他,嗯 题目描述 ZRQ发现这里有 \(N\) 块排成一排的 ...

  5. [洛谷P5137]polynomial

    题目大意:求:$$\sum\limits_{i=0}^na^{n-i}b^i\pmod{p}$$$T(T\leqslant10^5)$组数据,$a,b,n,p\leqslant10^{18}​$ 题解 ...

  6. Mybatis笔记一：java.lang.NoClassDefFoundError: org/apache/ibatis/mapping/DatabaseIdProvider

    异常错误:org.springframework.beans.factory.BeanCreationException: Error creating bean with name 'sqlSess ...

  7. Alpha 冲刺 —— 十分之二

    队名 火箭少男100 组长博客 林燊大哥 作业博客 Alpha 冲鸭鸭! 成员冲刺阶段情况 林燊(组长) 过去两天完成了哪些任务 协调各成员之间的工作 协助前端界面的开发 搭建测试用服务器的环境 完成 ...

  8. 洛谷 P2056 [ZJOI2007]捉迷藏 解题报告

    P2056 [ZJOI2007]捉迷藏 题目描述 Jiajia和Wind是一对恩爱的夫妻,并且他们有很多孩子.某天,Jiajia.Wind和孩子们决定在家里玩捉迷藏游戏.他们的家很大且构造很奇特,由\ ...

  9. Hbase(四) 过滤器查询

    引言:过滤器的类型很多,但是可以分为两大类——比较过滤器,专用过滤器过滤器的作用是在服务端判断数据是否满足条件,然后只将满足条件的数据返回给客户端: 一.hbase过滤器的分类 1.比较过滤器 行键过 ...

  10. 【bzoj3173】最长上升子序列

    Portal --> bzoj3173 Solution 感觉自己需要智力康复qwq 首先题目给的这个序列肯定是一个\(1-n\)的排列,并且插入的顺序是从小到大 仔细思考一下会发现如果知道了最 ...