利用层序遍历（含空节点）和中序遍历重建二叉树 python

　　给定一颗二叉树的层序遍历（不含None的形式）和中序遍历序列，利用两个序列完成对二叉树的重建。

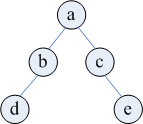
　　还是通过一个例子来说明整个过程，下图所示的二叉树，层序遍历结果为[a,b,c,d,e]，中序遍历结果为[d,b,a,c,e]，我们知道当我们找到根节点后，中序遍历能够提供给我们的信息就是左右子树分别包含哪些节点，而我们能否在层序遍历中找到根节点呢？

　　层序遍历是对每一层按照从左到右的顺序输出，那么对于一颗子树来说，如图中以b为根节点的左子树，其遍历顺序为b-d-None，实际上还是前序遍历的顺序，所以对于一棵子树的层序遍历序列，其第一个点就是这颗子树的根节点。而层序遍历的第一个节点必定是整棵树的根节点，以此在中序遍历中找到左右子树分别包含哪些节点之后，就可以在层序遍历中区分出左右子树的层序遍历结果，然后就可以分别开始重建子树，明显这是一个重复的过程，所以我们用递归调用实现。

　　首先还是定义二叉树的类

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

　　生成二叉树

class Solution:
     def buildtree(self,level,mid):
        if len(level)>0:
            root=TreeNode(level[0])#根节点
            rootid=mid.index(level[0])
            midleft=mid[:rootid]#左子树包含的节点
            midright=mid[rootid+1:]#右子树包含的节点
            levelleft,levelright=[],[]
            for node in level:
                if node in midleft:
                    levelleft.append(node)
                if node in midright:
                    levelright.append(node)
            root.left=self.buildtree(levelleft,midleft)
            root.right=self.buildtree(levelright,midright)
            return root

　　Python版本：3.6