[测试题]数组(array)

Description

Input

Output

Sample Input1

3 2 7
5 4 2

Sample Output1

999999732

Sample Explanation1

Sample Input2

5 3 1
5 4 3 5 5

Sample Output2

0

Sample Explanation2

Hint

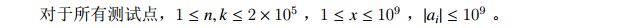
题解

由于负数是肯定小于正数的，我们首先想到的就是将乘积变成负数。我们可以统计输入的负数个数。

那么会有两种情况：

$(i)$无论怎么变变不了负数，这个时候我们将所有数取绝对值。

我们需要使乘积最小，这时只需要将绝对值最小的数减小即可。

证明：

假设有四个正整数$a_1,a_2,a_3,a_4$，满足$a_1<a_2<a_3<a_4$。需要减去$x$。

我们取极端情况若$a_1-x$：

原式$=(a_1-x)*a_2*a_3*a_4$

　　$=a_1*a_2*a_3*a_4-x*a_2*a_3*a_4$

若$a_4-x$：

原式$=a_1*a_2*a_3*(a_4-x)$

　　$=a_1*a_2*a_3*a_4-x*a_1*a_2*a_3$

由于$-x*a_2*a_3*a_4<-x*a_1*a_2*a_3$

显然得证。

$(ii)$可以变成负数，我们变完负数后同样将所有数取绝对值。

既然已经是负数了，那我们只需所有的数的绝对值积最大即可。

证明同上，只是改变了加减。

所以我们只需要用小根堆维护绝对值最小的数即可。

我是用两个堆分别维护正数和负数。同时注意不要边减边取模，因为保存的是绝对值，和负数直接取模不同。

详见代码。

 #include<map>
 #include<ctime>
 #include<cmath>
 #include<queue>
 #include<stack>
 #include<vector>
 #include<string>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<iostream>
 #include<algorithm>
 #define LL long long
 #define RE register
 #define IL inline
 using namespace std;
 const LL N=2e5;
 const LL MOD=1e9+;

 priority_queue<LL, vector<LL>, greater<LL> >a,b;
 LL n,k,x,ai;
 LL cnt;
 bool flag;
 IL void print()
 {
     LL sum=;
     while (!a.empty())
     {
         LL tmp=-a.top()%MOD;a.pop();
         sum=(sum*tmp)%MOD;
     }
     while (!b.empty())
     {
         LL tmp=b.top()%MOD;b.pop();
         sum=(sum*tmp)%MOD;
     }
     printf("%lld\n",(sum+MOD)%MOD);
     exit();
 }
 IL void cuta()
 {
     if (a.top()/x+(bool)(a.top()%x)>=k)
     {
         LL tmp=a.top();a.pop();
         tmp=(tmp-(LL)k*(LL)x/*%MOD*/)/*%MOD*/;
         a.push(tmp);
         print();
     }
     else
     {
         LL tmp=a.top();a.pop();
         tmp=(tmp-(LL)(a.top()/x+(bool)(a.top()%x))*(LL)x)/*%MOD*/;
         k-=a.top()/x+(bool)(a.top()%x);
         b.push(-tmp);
     }
 }
 IL void cutb()
 {
     if (b.top()/x+(bool)(b.top()%x)>=k)
     {
         LL tmp=b.top();b.pop();
         tmp=(tmp-(LL)k*(LL)x/*%MOD*/)/*%MOD*/;
         b.push(tmp);
         print();
     }
     else
     {
         LL tmp=b.top();b.pop();
         tmp=(tmp-(LL)(b.top()/x+(bool)(b.top()%x))*(LL)x)/*%MOD*/;
         k-=b.top()/x+(bool)(b.top()%x);
         a.push(-tmp);
     }
 }
 IL LL getnum()
 {
     if (a.empty()) {flag=;LL tmp=b.top();b.pop();return tmp;}
     if (b.empty()) {flag=;LL tmp=a.top();a.pop();return tmp;}
     if (a.top()>b.top()) {flag=;LL tmp=b.top();b.pop();return tmp;}
     {flag=;LL tmp=a.top();a.pop();return tmp;}
 }

 int main()
 {
     scanf("%lld%lld%lld",&n,&k,&x);
     for (RE LL i=;i<=n;i++)
     {
         scanf("%lld",&ai);
         if (ai<) cnt++,a.push(-ai);
         else b.push(ai);
     }
     if (cnt%==)
     {
         if (cnt==) cutb();
         else if (cnt==n) cuta();
         else
         {
             if (a.top()>=b.top()) cutb();
             else cuta();
         }
     }
     if (!k) print();
     while (k--)
     {
         LL tmp=getnum();
         tmp=(tmp+x)/*%MOD*/;
         if (flag) a.push(tmp);
         else b.push(tmp);
     }
     print();
     return ;
 }