Luogu P3960 列队(动态开点线段树)

P3960 列队

题意

题目描述

Sylvia 是一个热爱学习的女孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia所在的方阵中有\(n \times m\)名学生，方阵的行数为\(n\)，列数为\(m\)。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中的学生从\(1\)到\(n \times m\)编上了号码（参见后面的样例）。即：初始时，第\(i\)行第\(j\)列的学生的编号是\((i-1) \times m + j\)。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了\(q\)件这样的离队事件。每一次离队事件可以用数对\((x,y)(1 \le x \le n, 1 \le y \le m)\)描述，表示第\(x\)行第\(y\)列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：

向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第\(x\)行第\(m\)列。

向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第\(n\)行第\(m\)列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第\(n\)行第\(m\)列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以Sylvia想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：

输入共\(q+1\)行。

第\(1\)行包含\(3\)个用空格分隔的正整数\(n,m,q\)，表示方阵大小是\(n\)行\(m\)列，一共发生了\(q\)次事件。

接下来\(q\)行按照事件发生顺序描述了\(q\)件事件。每一行是两个整数\(x,y\)，用一个空格分隔，表示这个离队事件中离队的学生当时排在第\(x\)行第\(y\)列。

输出格式：

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。

输入输出样例

输入样例：

2 2 3
1 1
2 2
1 2

输出样例：

1
1
4

说明

【输入输出样例说明】

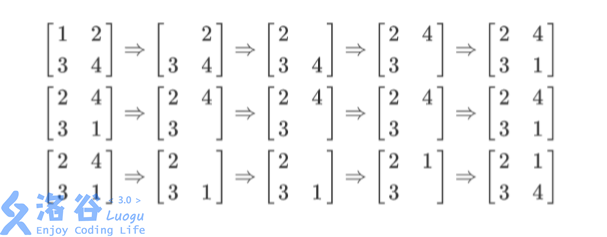
列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为\(1\)的同学离队，这时空位在第一行第一列。接着所有同学向左标齐，这时编号为\(2\)的同学向左移动一步，空位移动到第一行第二列。然后所有同学向上标齐，这时编号为\(4\)的同学向上一步，这时空位移动到第二行第二列。最后编号为\(1\)的同学返回填补到空位中。

【数据规模与约定】

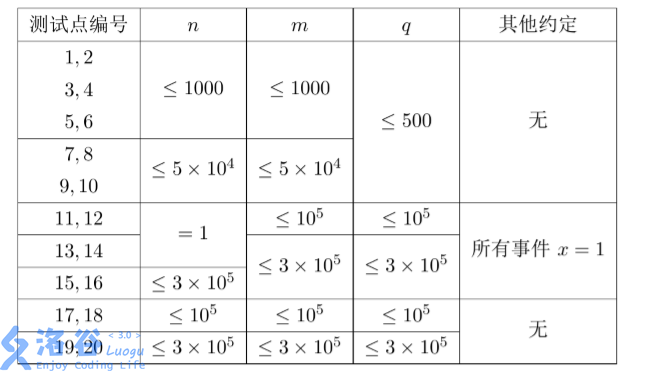
数据保证每一个事件满足\(1 \le x \le n,1 \le y \le m\)

思路

wwx你在做什么？ --diggersun

列队。 --logeadd

...

wwx列队怎么做呀？ --Uranus

你可以对每一排开一棵\(Splay\)，然后用动态开点优化空间...诶你别走啊！ --logeadd

身为蒟蒻的我不会任何高级数据结构，所以只能用简单的线段树做了这道题。

然而这题空间上有限制，只能用动态开点线段树了。今天晚上用这道题做模板，学习了动态开点，顺便也做了这道题。

进入正题。我们先思考题目操作的意义：

1. 离队一个人，相当于单点询问和删除。
2. 向左看齐，相当于该行的最后一列少了一个人，最后一列的该行少了一个人。
3. 向前看齐后离队人进队，相当于最后一列结尾添加了一个人。

Q：那么什么数据结构支持单点询问、单点删除、单点添加呢？

A：\(Splay\)（被打死

A：线段树和树状数组（正解！

根据对于操作的分析，我们在每一行的前\((m-1)\)个位置开一棵线段树，再对于最后一列单独开一棵线段树，就能完成所有操作了。

具体实现的话，我们在线段树的每一个结点上用\(sz\)数组储存该结点下还有多少个人，删点时直接暴力移除对应位置上的点，然后\(update\)时每个祖先节点的\(sz\)都减一，查询时按照\(sz\)左右跳查找，加点时向线段树的末尾处加入一个点即可。

再来思考空间问题。对于线段树的大小，因为有\(q\)次询问，最坏情况下全部插入操作在同一行，所以我们每一行线段树的大小是\((m+q)\)的，每一列线段树的大小是\((n+q)\)的，总的空间大小为\(((m+q)(n-1)+(n+q))\)，而单是一个\(m \times n\)的空间我们已经承受不住了，期望得分也只有\(70\)了，这对于要AK比赛的logeadd巨佬来说是显然不够的所以我们要运用一个优秀的操作：动态开点。

想想普通线段树的\(lazytag\)标签的意义：如果我查询到了这个结点，那么我就\(pushdown\)，因为只有这种情况下该结点以及其儿子结点才有可能对答案有贡献；相反，如果我一直不查询这个结点，我就只保存更新的值而不向下传递，因为此时这个值对于答案好毫无贡献。而动态开点也一样，如果我们一直没有询问一段区间，我们就一直不去建那个区间的结点。而一旦查询到了，我们就建结点。

实际操作起来是怎么样的呢？比如说我们查询单点，顺便把它删掉（你会发现在上面的分析中这两个操作总是连在一起的），就这么写：

LL get_sz(LL l,LL r)//先看下面那个函数
{
    if(now==n+1)//最后一列
    {
        if(r<=n) return r-l+1;//查询一开始就存在的区间，因为这一段还没有查询过，所以这一段上人是满的
        if(l<=n) return n-l+1;//r已经超过了区间，但是l还在区间中，而n是一开始就存在的人的结尾，所以总数是n-l+1
        return 0;//都是新结点，在任何操作之前都没有人
    }//在行数上建立的结点
    if(r<m) return r-l+1;//在之前就存在，同上
    if(l<m) return m-l;//在之前有一部分存在，同上
    return 0;//全都不存在，同上
}
LL ask(LL &id,LL l,LL r,LL x)//id为当前结点编号，l,r为当前区间，x为要查询的点在线段树上的位置
{
    if(!id)//还没有开这个点的情况
    {
        id=++cnt;//开点
        sz[id]=get_sz(l,r);//获取当前结点管理的区间中的人数
        if(l==r)//到了最后一个点，要记录人的编号了
        {
            if(now==n+1) val[id]=l*m;//最后一列的编号统计
            else val[id]=(now-1)*m+l;//第一列的编号统计
        }
    }
    sz[id]--;//这一段要少个人，直接--
    if(l==r) return val[id];//找到那个人了，溜了溜了
    LL mid=(l+r)>>1;//继续往下找qwq
    if((!ls[id]&&x<=(mid-l+1))||sz[ls[id]]>=x) return ask(ls[id],l,mid,x);//在左儿子就能解决问题
    else//要找右儿子才能解决问题
    {
        if(!ls[id]) x-=(mid-l+1);//统计差多少个人在能找到
        else x-=sz[ls[id]];//同上
        return ask(rs[id],mid+1,r,x);//往右儿子找
    }
}

同样的，我们处理单点加入时这样处理：

void change(LL &id,LL l,LL r,LL x,LL v)//x还是表示插入位置，v为插入的权值
{
    if(!id)//建点
    {
        id=++cnt;//操作都是一样的
        sz[id]=get_sz(l,r);
        if(l==r) val[id]=v;//这里就不用特判是在最后一列还是别的了
    }
    sz[id]++;
    if(l==r) return ;//改完了，溜了溜了
    LL mid=(l+r)>>1;
    if(x<=mid) change(ls[id],l,mid,x,v);//只要改左儿子
    else change(rs[id],mid+1,r,x,v);//只要改右儿子
}

主要代码就到这里结束了，其实码量也不大不是吗？不过还是希望今年的数据结构题能简单一点\(qwq\)。

怨念--;

NOIP rp++;

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN=3e5+5;
const LL MAXM=1e7;
LL n,m,q,p,now;
LL cnt,rt[MAXN],ord[MAXN],sz[MAXM],ls[MAXM],rs[MAXM],val[MAXM];
LL read()
{
    LL re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
LL get_sz(LL l,LL r)
{
    if(now==n+1)
    {
        if(r<=n) return r-l+1;
        if(l<=n) return n-l+1;
        return 0;
    }
    if(r<m) return r-l+1;
    if(l<m) return m-l;
    return 0;
}
LL ask(LL &id,LL l,LL r,LL x)
{
    if(!id)
    {
        id=++cnt;
        sz[id]=get_sz(l,r);
        if(l==r)
        {
            if(now==n+1) val[id]=l*m;
            else val[id]=(now-1)*m+l;
        }
    }
    sz[id]--;
    if(l==r) return val[id];
    LL mid=(l+r)>>1;
    if((!ls[id]&&x<=(mid-l+1))||sz[ls[id]]>=x) return ask(ls[id],l,mid,x);
    else
    {
        if(!ls[id]) x-=(mid-l+1);
        else x-=sz[ls[id]];
        return ask(rs[id],mid+1,r,x);
    }
}
void change(LL &id,LL l,LL r,LL x,LL v)
{
    if(!id)
    {
        id=++cnt;
        sz[id]=get_sz(l,r);
        if(l==r) val[id]=v;
    }
    sz[id]++;
    if(l==r) return ;
    LL mid=(l+r)>>1;
    if(x<=mid) change(ls[id],l,mid,x,v);
    else change(rs[id],mid+1,r,x,v);
}
int main()
{
    n=read(),m=read(),q=read();
    p=max(n,m)+q;
    while(q--)
    {
        LL x=read(),y=read(),z;
        if(y==m) now=n+1,z=ask(rt[now],1,p,x);
        else now=x,z=ask(rt[now],1,p,y);
        printf("%lld\n",z);
        now=n+1;
        change(rt[now],1,p,n+(++ord[now]),z);
        if(y!=m)
        {
            z=ask(rt[now],1,p,x),now=x;
            change(rt[now],1,p,m-1+(++ord[now]),z);
        }
    }
    return 0;
}