洛谷P4526 【模板】自适应辛普森法2

P4526 【模板】自适应辛普森法2

洛谷传送门

题目描述

计算积分

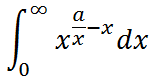
保留至小数点后5位。若积分发散，请输出"orz"。

输入格式

一行，包含一个实数，为a的值

输出格式

一行，积分值或orz

输入输出样例

输入 #1复制

2.33

输出 #1复制

1.51068

说明/提示

a<=50

请注意时空限制。

Solution

这和辛普森公式又啥关系？上限可是正无穷!

带着好奇心，我打开了几何画板。

几何画板

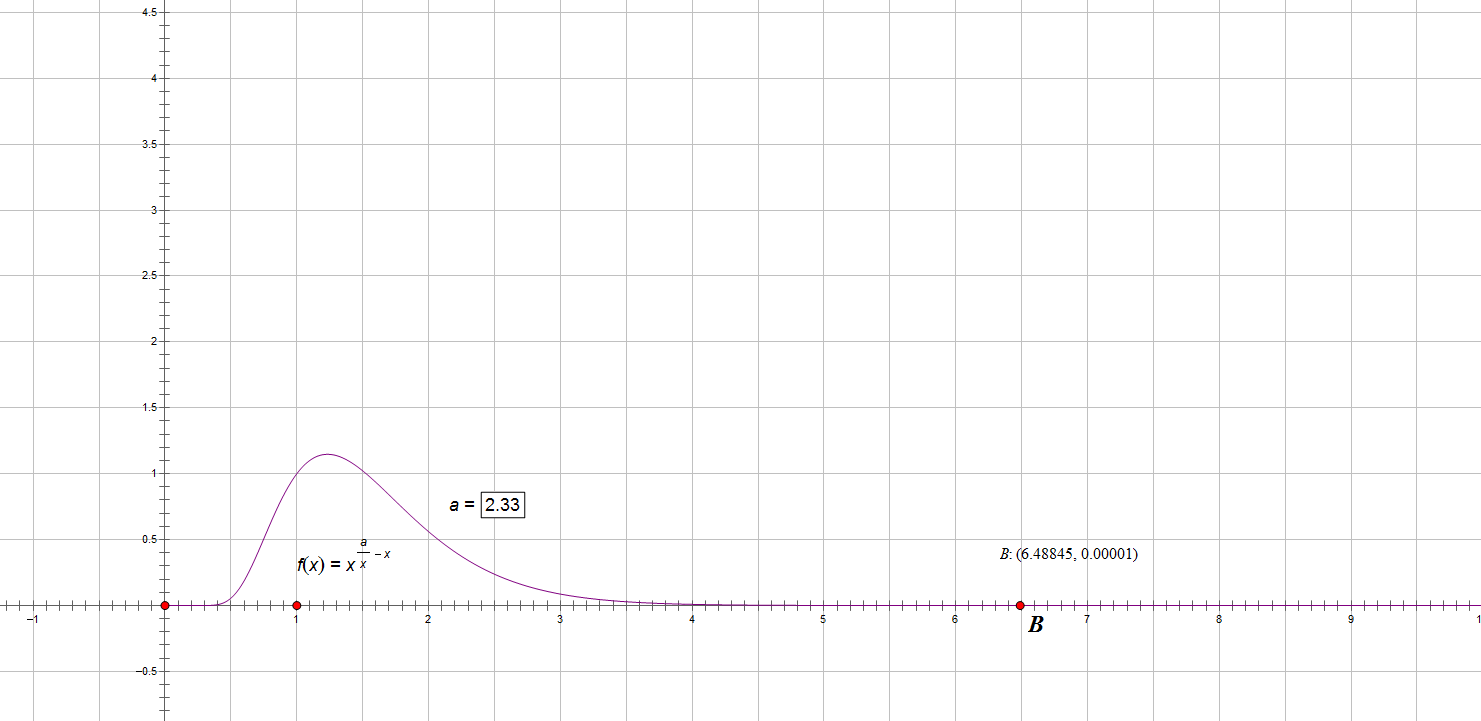
这……这么快就收敛了？！？！？！

看看a=50？

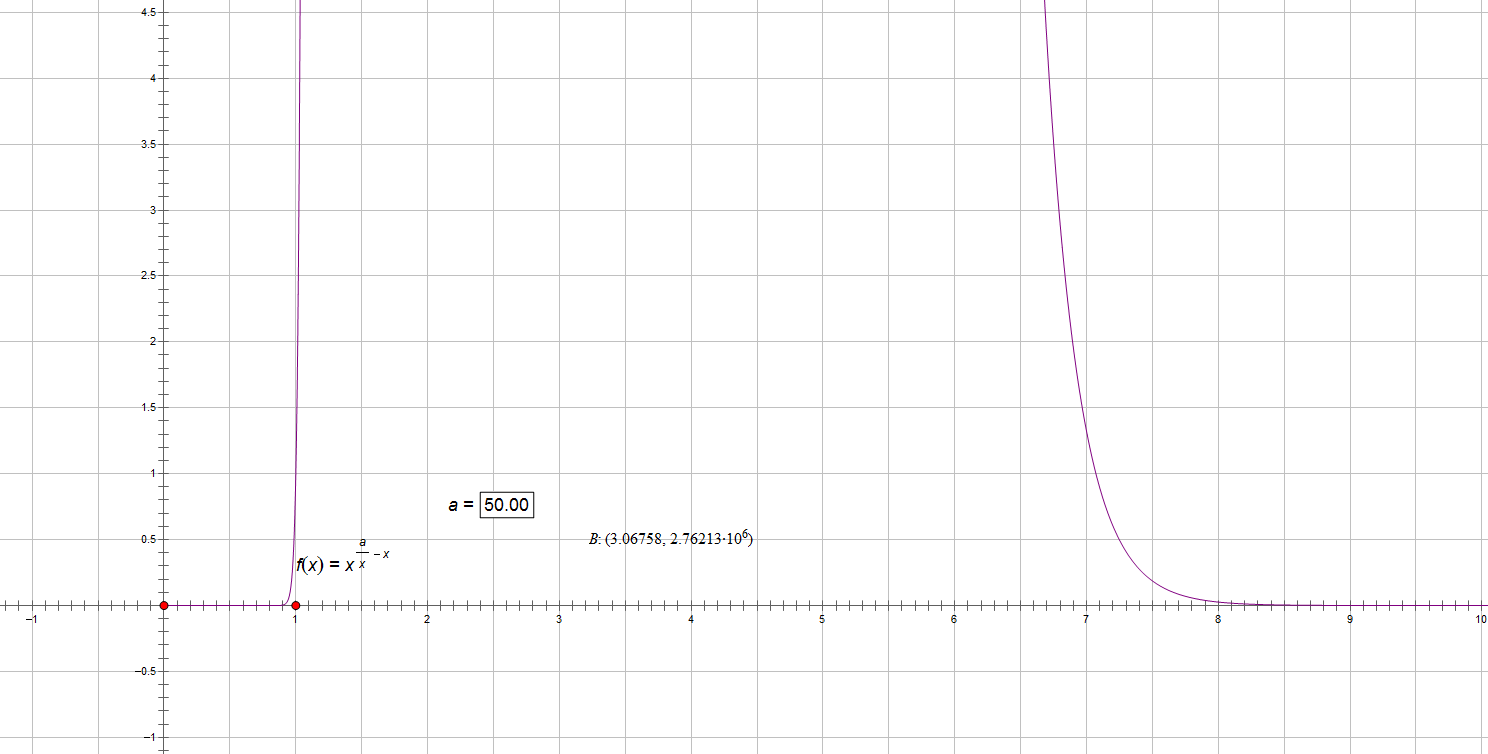
随便把B放在3边上。结果……反正是有限的，有限的就好。

貌似在x=10附近，这玩意就收敛的可怜了……

你有没有考虑a<0？

把B靠近原点，再把a调为-1。

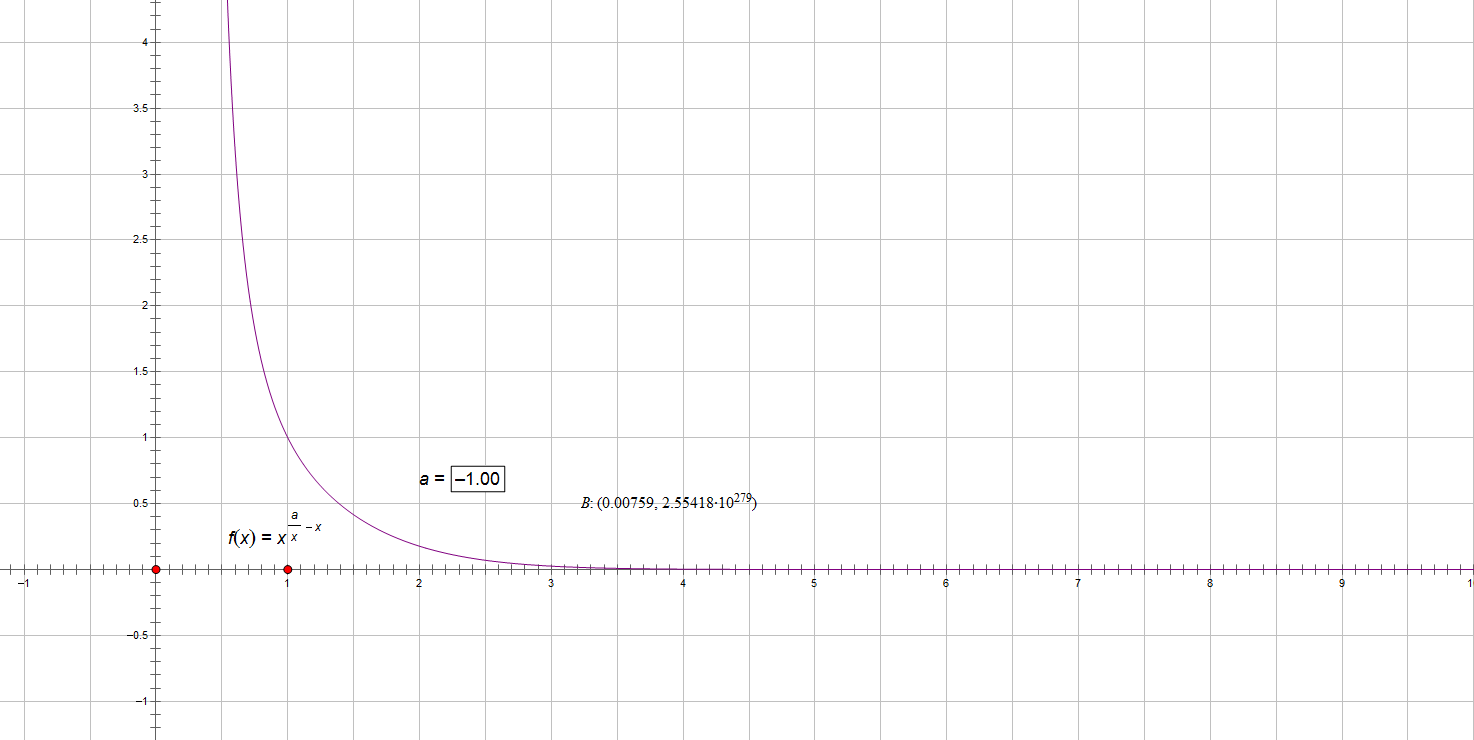
不能想，要是B的横坐标为0会发生什么……貌似直接不显示B点了……

几何画板——自保系统？

从这里就可以得到：

1. a<0时函数发散
2. a>0时函数收敛于20左右（确保误差尽量小，建议稍大一点）

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#define IL inline
#define re register
using namespace std;
const double eps=1e-;
double a;
IL double f(double x)
{
    return pow(x,a/x-x);
}
IL double simpson(double l,double r)
{
    return (r-l)*(f(l)+4.0*f((l+r)/2.0)+f(r))/6.0;
}
double integral(double l,double r)
{
    re double mid=(l+r)/,ans=simpson(l,r);
    if(fabs(ans-simpson(l,mid)-simpson(mid,r))<eps) return (ans+simpson(l,mid)+simpson(mid,r))/2.0;
    return integral(l,mid)+integral(mid,r);
}
int main()
{
    cin>>a;
    if(a<) cout<<"orz";
    else printf("%.5lf",integral(eps,));
    return ;
}

Attention

保留5位小数