康拓展开 & 逆康拓展开 知识总结(树状数组优化)

康拓展开 :

康拓展开,难道他是要飞翔吗？哈哈,当然不是了,康拓具体是哪位大叔,我也不清楚,重要的是
我们需要用到它后面的展开,提到展开,与数学相关的,肯定是一个式子或者一个数进行分解,即
展开。
到底是什么样的式子才配的上这么高大尚的名字？

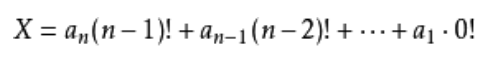
其中, a[i]为整数，并且0 <= a[i] <= i, 0 <= i < n, 表示当前未出现的的元素中排第几个，这就是康托展开。

就是这样一个神奇的式子,我们发现每项后面都有一个 ！, 说明这个式子可能跟阶乘有关,跟阶乘虽然有关,但
跟递归关系可不大哦。

康托展开是一个全排列到一个自然数的双射，常用于构建hash表时的空间压缩。
设有n个数（1，2，3，4,…,n），可以有组成不同(n!种)的排列组合.
康托展开表示的就是是当前排列组合在n个不同元素的全排列中的名次

解决哪些问题？

1、全排列问题(数字排列,字符排列,and so on)
2、Hash 函数

康托展开与逆康托展开之间的关系 ?

两者是双射的关系,通俗来讲就是类似乘法和除法的关系,
比如 12345,这样一个数, 我们可以先通过乘法得到,
0 * 10 + 5 + 4 * 10 + 4 + 3 * 100 + 2 * 1000 + 1 * 10000;
同时,我们得到这个整数后也可以通过 / 10 与 % 10 进行拆分成每一个
数。(可能解释的不是十分到位,可以自己再琢磨琢磨)

康托展开怎么求呢 ？

1、通过知道一个排列,然后可以得到这个排列在全排列中的排名。
   具体来说就是 : 比如 1234 ,那么 1243 再由这 4 个数中
   组成的排名 是 2 (1234 如果是排名 1 的话,实际上康托展开
   的排名是从 0 开始的,所以我们最后的排名的时候习惯 + 1,为
   啥会是从 0 开始的,下面会进行详细的解释)

2、康托展开怎么求呢 ？
在（1，2，3，4，5）5个数的排列组合中，计算 34152的康托展开值。
首位是3，则小于3的数有两个，为1和2，a[5]=2，则首位小于3的所有排列组合为 a[5]*(5-1)!
第二位是4，则小于4的数有两个，为1和2，注意这里3并不能算，因为3已经在第一位，所以其实计算的是在第二位之后小于4的个数。因此a[4]=2
第三位是1，则在其之后小于1的数有0个，所以a[3]=0
第四位是5，则在其之后小于5的数有1个，为2，所以a[2]=1
最后一位就不用计算啦，因为在它之后已经没有数了，所以a[1]固定为0
根据公式：
X = 2 * 4! + 2 * 3! + 0 * 2! + 1 * 1! + 0 * 0! = 2 * 24 + 2 * 6 + 1 = 61
所以比 34152 小的组合有61个，即34152是排第62。

逆康托展开怎么求呢 ?

在（1，2，3，4，5）给出61可以算出起排列组合为 34152。由上述的计算过程可以容易的逆推回来，具体过程如下：
用 61 / 4! = 2余13，说明a[5]=2,说明比首位小的数有2个，所以首位为3。
用 13 / 3! = 2余1，说明a[4]=2，说明在第二位之后小于第二位的数有2个，所以第二位为4。
用  1 / 2! = 0余1，说明a[3]=0，说明在第三位之后没有小于第三位的数，所以第三位为1。
用  1 / 1! = 1余0，说明a[2]=1，说明在第二位之后小于第四位的数有1个，所以第四位为5。
最后一位自然就是剩下的数2啦。
通过以上分析，所求排列组合为 34152。

为什么康托展开的排名是从 0 开始的 ？

那 1234 来说:
1234 的康托展开为 : 0 * 3! + 0 * 2! + 0 * 1! + 0 * 0! = 0
(比 1 小的数有 0 个, 1 用掉后, 比 2 小的数也剩下 0 个,后面依次类推,得到的值是 0)
所以排名是从 0 开始的,但是我们说排名时习惯从 1 开始,所以会在最后序列得出的时候 + 1.

应用:

1、给定一个自然数集合组合一个全排列，所其中的一个排列组合在全排列中从小到大排第几位。
   在上述例子中，在（1，2，3，4，5）的全排列中，34152的排列组合排在第62位。

2、反过来，就是逆康托展开，求在一个全排列中，从小到大的第n个全排列是多少。
比如求在（1，2，3，4，5）的全排列中，第62个排列组合是34152。[注意具体计算中，要先 -1 才是其康托展开的值。]

3、另外康托展开也是一个数组到一个数的映射，因此也是可用于hash，用于空间压缩。比如在保存一个序列，
   我们可能需要开一个数组，如果能够把它映射成一个自然数， 则只需要保存一个整数，大大压缩空间。比如八数码问题。

参考链接:

wbin233 大佬 : https://blog.csdn.net/wbin233/article/details/72998375

Code：

康托展开:

// 阶乘
void init_fac() {
	fac[0] = 1;
	for(int i = 1; i <= 12; i ++) {
		fac[i] = fac[i - 1] * i;
	}
}

LL cantor() {
	int len = strlen(a);
	for(int i = 0; i < len; i ++) {
		LL temp = 0;
		for(int j = i + 1; j < len; j ++) {
                        // 找到所有未使用过的数中比当前数小的个数
			if(a[j] < a[i]) temp ++;
 		}
 		res += temp * fac[len - i - 1];
	}
	return res + 1; // 返回排名(是从 0 开始的,所以需要 + 1)
}

树状数组优化:

/*
       为什么用树状数组(线段树也可以)？
       1、求前缀和
       2、支持在线修改
       我们可以通过预处理求取前缀和,每个数比它小的就是数量就是其 本身的值 - 1
        树状数组经过预处理后 C 数组可能是这样的 :
        1 2 3 4 5 6 7
        那么比 3 小的个数有几个呢？实际上就是本身的前缀和 - 1即可
*/

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define MOD 998244353

using namespace std;

typedef long long LL;
const int maxn = 1e6 + 10;

int a[maxn],c[maxn];
LL fac[maxn];

LL res = 0;
int n;

int main(void) {
	void add(int x,int v);
	int query(int x);
	void init_fac();
	LL cantor();
	scanf("%d",&n);
	init_fac();
	for(int i = 1; i <= n; i ++) {
		scanf("%d",&a[i]);
                // - 1 是因为排名是从 0 开始的
		res = (res + query(a[i] - 1) * fac[n - i] );
		add(a[i],-1);  // 这个数用掉过后就不能用了,所以它后面比它大(比这些大的的小的 的数量就会 -1)
                               // 可能有点绕, 比如 1 2 3 4 5,用掉 2 后,后面比 3 小的数量就减少了一个
	}
	cout << res + 1 << endl;
	return 0;
}

int lowbit(int x) {
	return x & -x;
}

void add(int x,int v) {
	for(int i = x; i <= n; i += lowbit(i)) {
		c[i] += v;
	}
	return ;
}
void init_fac() {
	fac[0] = 1;
	for(int i = 1; i <= n; i ++) {
		fac[i] = (fac[i - 1] * i);
		add(i,1);  // 求前缀和
	}
	return;
}
int query(int x) {
	int res = 0;
	for(int i = x; i ; i -= lowbit(i)) {
		res += c[i];
	}
	return res;
}

逆康托展开:

void decantor(int x, int n)
{
    vector<int> v;  // 存放当前可选数
    vector<int> a;  // 所求排列组合
    for(int i=1;i<=n;i++)
        v.push_back(i);
    for(int i=m;i>=1;i--)
    {
        int r = x % FAC[i-1];
        int t = x / FAC[i-1];
        x = r;
        sort(v.begin(),v.end());// 从小到大排序
        a.push_back(v[t]);      // 剩余数里第t+1个数为当前位
        v.erase(v.begin()+t);   // 移除选做当前位的数
    }
}

树状数组 + 二分 优化:

LL Check(LL l,LL r,LL aim) {
	while(l < r) {
		LL mid = (l + r) >> 1;
		if(query(mid) - 1 >= aim) {
			r = mid;
		} else {
			l = mid + 1;
		}
	}
	return r;
}

void reCantor() {
	pos --;   // 需要先 -- (排名从 0 开始)
	for(LL i = 1,num = n - 1; i <= n; num --, i ++) {
		LL aim = pos / fac[num];                     // 找 第 k 大的数
		pos = pos % fac[num];
		LL t = Check(1,n,aim);
		cout << t << " ";
		add(t ,-1);                 // 与上面的解释一样
	}
	cout << endl;
	return ;
}

例题 :

1、Dictionary:

https://vjudge.net/problem/CSU-1828#author=0

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 12;

typedef long long LL;

char str[maxn];
LL fac[maxn];
LL res = 0;
int T;

int main(void) {
	LL kangtuo();
	void init_fac();
	init_fac();
	scanf("%d",&T);
	while(T --) {
		res = 0;
		cin >> str;
		res = kangtuo();
		cout << res << endl;
	}
	return 0;
} 

void init_fac() {
	fac[1] = 1;
	for(int i = 2; i <= 12; i ++) {
		fac[i] = fac[i - 1] * i;
	}
	return ;
}

LL kangtuo() {
	int len = strlen(str);
	for(int i = 0; i < len; i ++) {
		LL temp = 0;
		for(int j = i + 1; j < len; j ++) {
			if(str[j] < str[i]) temp ++;
		}
		res += temp * fac[len - i - 1];
	}
	return res + 1;
}

2、Uim的情人节礼物·其之弐

https://www.luogu.com.cn/problem/P2524

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 10;

typedef long long LL;

LL fac[maxn];
char a[maxn];

int n;
LL res = 0;
int main(void) {
	void init_fac();
	LL cantor();
	init_fac();
	cin >> n >> a;
	res = 0;
	res = cantor();
	cout << res << endl;
	return 0;
}

void init_fac() {
	fac[0] = 1;
	for(int i = 1; i <= 12; i ++) {
		fac[i] = fac[i - 1] * i;
	}
}

LL cantor() {
	int len = strlen(a);
	for(int i = 0; i < len; i ++) {
		LL temp = 0;
		for(int j = i + 1; j < len; j ++) {
			if(a[j] < a[i]) temp ++;
 		}
 		res += temp * fac[len - i - 1];
	}
	return res + 1;
}

3、【模板】康托展开(树状数组优化)

https://www.luogu.com.cn/problem/P5367

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define MOD 998244353

using namespace std;

typedef long long LL;
const int maxn = 1e6 + 10;

int a[maxn],c[maxn];
LL fac[maxn];

LL res = 0;
int n;

int main(void) {
	void add(int x,int v);
	int query(int x);
	void init_fac();
	LL cantor();
	scanf("%d",&n);
	init_fac();
	for(int i = 1; i <= n; i ++) {
		scanf("%d",&a[i]);
		res = (res % MOD + ((query(a[i] - 1)) % MOD * fac[n - i] % MOD) % MOD );
		add(a[i],-1);  // 用过的就不能再用了
	}
	cout << res + 1 << endl;
	return 0;
}

int lowbit(int x) {
	return x & -x;
}

void add(int x,int v) {
	for(int i = x; i <= n; i += lowbit(i)) {
		c[i] += v;
	}
	return ;
}
void init_fac() {
	fac[0] = 1;
	for(int i = 1; i <= n; i ++) {
		fac[i] = (fac[i - 1] % MOD * i % MOD)% MOD;
		add(i,1);
	}
	return;
}

int query(int x) {
	int res = 0;
	for(int i = x; i ; i -= lowbit(i)) {
		res += c[i];
	}
	return res;
}

4、[USACO11FEB]牛线Cow Line：

https://www.luogu.com.cn/problem/P3014

(康托展开 & 逆康托展开的综合应用)

(坑不少,卡long long)

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int maxn = 100;

LL fac[maxn],c[100];   // 全部用 long long
LL a[maxn];;

LL res = 0;
LL T,n,pos;
char op;

int main(void) {
	LL cantor();
	void add(LL x,LL v);
	void reCantor();
	void init_fac();
	scanf("%lld%lld",&n,&T);
	while(T --) {
		cin >> op;
		init_fac();
		if(op == 'Q') {
			memset(c,0,sizeof(c));
			for(LL i = 1; i <= n; i ++) {
				scanf("%lld",&a[i]);
				add(i,1);
			}
			res = 0;
			res = cantor();
			cout << res << endl;
		} else {
			memset(c,0,sizeof(c));
			for(LL i = 1; i <= n; i ++) {
				add(i,1);
			}
			scanf("%lld",&pos);
			reCantor();
		}
	}
	return 0;
}
LL lowbit(LL x) {
	return x & -x;
}

void add(LL x,LL v) {
	for(LL i = x; i <= n; i += lowbit(i)) {
		c[i] += v;
	}
	return ;
}
void init_fac() {
	fac[0] = 1;
	for(LL i = 1; i <= n; i ++) {
		fac[i] = fac[i - 1] * i;
	}
	return ;
}

LL query(LL x) {
	LL res = 0;
	for(LL i = x; i ; i -= lowbit(i)) {
		res += c[i];
	}
	return res;
}

LL cantor() {
	LL res = 0;
	for(LL i = 1; i <= n; i ++) {
		res += (query(a[i] - 1) * fac[n - i]);
		add(a[i],-1);
	}
	return res + 1;                             // 不要忘记 + 1
}

LL Check(LL l,LL r,LL aim) {
	while(l < r) {
		LL mid = (l + r) >> 1;
		if(query(mid) - 1 >= aim) {
			r = mid;
		} else {
			l = mid + 1;
		}
	}
	return r;
}

void reCantor() {
	pos --;
	for(LL i = 1,num = n - 1; i <= n; num --, i ++) {
		LL aim = pos / fac[num];                     // 找 第 k 大的数
		pos = pos % fac[num];
		LL t = Check(1,n,aim);
		cout << t << " ";
		add(t ,-1);
	}
	cout << endl;
	return ;
}