HDU 5531

题目大意：

给定一个n边形的顶点

以每个顶点为圆心画圆（半径可为0）

每个顶点的圆要和它相邻顶点的圆相切（不相邻的可相交）

求所有圆的最小面积总和并给出所有圆的半径

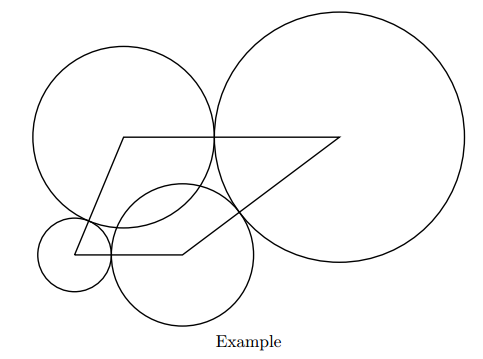
设半径为r1 r2 ... rn，顶点距离为L1 L2 ... Ln

当顶点数为奇数时 由

r1+r2=L1

r2+r3=L2

......

rn+r1=Ln

可得 r1+r1=L1-L2+L3-......+Ln

只要中间所有半径 r >= 0 那么r1就有唯一解

当顶点数为偶数时 由

r1+r2=L1

r2+r3=L2

......

rn+r1=Ln

可得 0=L1-L2+L3-......-Ln

即 L1+L3+...+Ln-1=L2+L4+...+Ln 时 才有解

由 上式可得

r2=L1-r1

r3=L2-L1+r1

......

r1=Ln-......+r1

也就是每个 r 都可以转换为

第偶数个顶点时 r=x+r1 或

第奇数个顶点时 r=x-r1 的形式

已知 r>=0 得

第偶数个顶点时 x+r1>=0 即 r1>=-x

第奇数个顶点时 x-r1>=0 即 r1<=x

那么由所有顶点的约束 就能得到r1的范围 [L,R]

圆的面积总和 S=PI*(r1^2+r2^2+r3^2+...+rn^2)

而每个r^2都可以转换为 r^2=(r1+x)^2  或 r^2=(r1-x)^2

如： r2^2=(r1-L1)^2, r3^2=(r1+L2-L1)^2

即 递推时 x=Li-x

第偶数个顶点时 ri^2=(r1-x)^2

第奇数个顶点时 ri^2=(r1+x)^2

那么 S=PI*（a*r1^2+b*r1+c）

如： r2^2=(r1-L1)^2, r3^2=(r1+L2-L1)^2

​    ​则 S1=PI*(1*r1^2+0*r1+0) (a=1,b=0,c=0,x=0)

​    ​S2=PI*（S1+r2^2）=PI*（S1+(r1-x)^2）

​    ​    ​=PI*（S1+r1^2-2*x*r1+x*x） (a=a+1，b=b+(-1)*2*x，c=c+x*x，x=L1-x)

​    ​S3=PI*（S2+r3^2）=PI*（S2+(r1+x)^2）

​    ​    ​=PI*（S1+r1^2+2*x*r1+x*x） (a=a+1，b=b+(1)*2*x，c=c+x*x，x=L2-x)

即

第偶数个顶点时 a+=1，b+=(-1)*2*x，c+=x*x，x=Li-x

第奇数个顶点时 a+=1，b+=1*2*x，c+=x*x，x=Li-x

又 a*r1^2+b*r1+c=0 时存在极值点 1-b/(2*a)

再与r1的范围比较一下 就能得到r1 从而得到S的最小值

或者直接利用[L,R] 用三分法求解

#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;

const double eps = 1e-;
const double PI = acos(-1.0);
double add(double a,double b) {
    if(abs(a+b)<eps*(abs(a)+abs(b))) return ;
    return a+b;
}
struct P {
    double x,y;
    P(){};
    P(double _x,double _y):x(_x),y(_y){}
    P operator - (P p) {
        return P(add(x,-p.x),add(y,-p.y));
    }
    double dot(P p) {
        return add(x*p.x,y*p.y);
    }
}p[];
int n;
double ans;
double r[], len[];
double lenV(P p) {
    return sqrt(p.dot(p));
}
double getArea(double r0) {
    double ans=; r[]=r0;
    for(int i=;i<n;i++) {
        if(r[i]<-eps) return ;
        ans+=r[i]*r[i];
        r[i+]=len[i]-r[i];
        //printf("len[i]%lf r[i]%lf\n",len[i],r[i]);
    }
    return ans*PI;
}

bool solve() {
    ll sum=;
    for(int i=;i<n;i++) {
        len[i]=lenV(p[(i+)%n]-p[i]);
        sum+= i% ? -len[i]:len[i];
    }
    if(n&) {
        double r0=sum/2.0;
        if(r0<-eps) return ;
        ans=getArea(r0);
        //printf("ans = %lf\n",ans);
    } else {
        if(sum) return ;
        ll a,b,c;
        a=b=c=;
        ll t=,L=,R=INF,k=;
        for(int i=;i<n;i++) {
            //printf("%lld %lld %lld\n",a,b,c);
            a++;
            b+=2.0*k*t;
            c+=t*t;
            if(k==) L=max(L,-t);
            else R=min(R,t);
            k*=-;
            t=len[i]-t;
        }
        if(L>R) return ;
        double mid=-b/2.0/a;
        mid=max(mid,(double)L);
        mid=min(mid,(double)R);
        ans=getArea(mid);
    }
    if(ans<eps) return ;
    return ;
}

int main()
{
    int t; scanf("%d",&t);
    while(t--) {
        scanf("%d",&n);
        for(int i=;i<n;i++)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        if(solve()) {
            printf("%.2f\n",ans);
            for(int i=;i<n;i++)
                printf("%.2f\n",r[i]);
        } else printf("IMPOSSIBLE\n");
    }

    return ;
}