CF1067C Knights 构造

题目链接：https://codeforc.es/contest/1067/problem/C

题意：有一个无限大的棋盘，棋盘上初始放置了\(n\)个国际象棋马。如果某一个格子没有放马且能够被\(4\)个及以上的马经一步走到，那么这个格子也会放一个马。（如下图，初始的7个马为绿色，然后我们发现可以在红色区域再放一个马，在红色区域放置后，蓝色区域也应该再放一个马，总共9个）构造一种初始\(n\)个马的放置方案，使得棋盘上最终马的数量大于\(\lfloor\frac{n^2}{10} \rfloor\)。

分析：一道相当有趣的构造。构造的关键在于我们如何去考虑这个\(\lfloor \frac{n^2}{10} \rfloor\)。首先先考虑一个国际象棋马能到达那些位置。如下图。

显然我们至少在黄色块中选择4个才能在绿色区域中放置一个马。于是我们应尽可能让这些红色区域连续出现，于是出现了一个最简单的构造，如下。

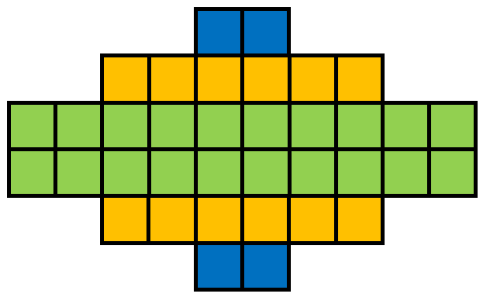
我们把这n个马均匀地分成两行放置（绿色区域）。那么问题来了，这种状态究竟能生成多少个马。观察上图，我们发现这个构造生成的马数呈等差数列关系。原先每行有\(\frac{n}{2}\)个马，而第一次生成马新增了\(2\cdot (\frac{n}{2} - 4)\)个马，第二次则是\(2\cdot (\frac{n}{2} - 8)\)，……

因此生成的总数为\(2\sum (\frac{n}{2} - 4i) = 2\cdot \frac{\frac{n}{2}(\frac{n}{2}\cdot \frac{1}{4})}{2} = \frac{n^2}{16}\)。因此这种构造的生成数不够，但是这个构造足以给我们启发，像这类向两侧生成的构造能够产生\(c\cdot n^2\)数量的马。于是我们考虑每一行最少几个马最终生成的数量才能多于\(\lfloor \frac{n^2}{10} \rfloor\)。

解不等式：\(2\sum (an- 4i)\leq \frac{n^2}{10}\)。

得到\(a\geq \frac{\sqrt{10}}{5}\)。于是我们需要构造一种新的方案使得每一行的马数能超过\(\frac{\sqrt{10}}{5}\)。如果对数字敏感一些则可发现\(\frac{2}{3}\geq \frac{\sqrt{10}}{5}\)，因此我们的目标就是构造出一种每行至少存在\(\frac{2n}{3}\)个马的方案。

于是我们看到了上图这种构造。每一行的马数量大约为\(\frac{n}{3}\)。虽然数量不够但我们马上可以发现这张图的很多地方都能放上一些马，如下。

　

每一行的个数上升到了\(\frac{2n}{3}-4\)。在忽略常数和一次项的影响后，总马数约为\(\frac{n^2}{8}\)。

　

AC代码：

#include<bits/stdc++.h>
#define rep(i, a, b) for(int i = a; i <= b; ++i)
using namespace std;
typedef	long long ll;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
ll n;
int main() {
	io(); cin >> n;
	rep(i, 1, n) cout << 2 * i / 3 << ' ' << 2 * i % 3 << endl;
}