O(n)空间复杂度,打印杨辉三角形的前n行
做小米的笔试题,给出一个整数n,求出它在杨辉三角形中第一次出现的行号。

想了半天,只能暴力法,从第1行开始找,一直找到第n行,若找得到则返回行号,若找不到则返回n+1(因为第n+1行第2列肯定是n)。当然,注意1是在第1行而不是第2行。更好的方法倒是没想到,倒是折腾出了打印杨辉三角形前n行的最优方法。
如果空间不限制的话,就直接定义二维数组a[n][n],初始时a[0][0]=1,通过a[i][j]=a[i-1][j]+a[i-1][j-1]计算即可。这里主要注意的就是边界条件,每一行首尾必须为1,只有夹在首尾中间的n-2个元素才适用于这个公式。
不过后来发现,只是打印的话,完全可以用2个一维数组来表示前一行和当前行。用vector表示的话就是v1和v2,每次通过v1计算出v2,打印完v2之后迭代(用v2给v1赋值)。后来发现除了vector可能重新分配的问题(这里可以vector初始化大小为n来解决),用v2给v1赋值还是很没必要的。
于是想到了可以直接交换指针,v1和v2分配足够大空间后就一直不改变大小,然后int* p1 = &v1[0]; int* p2 = &v2[0];然后每次迭代只需要std::swap(p1,p2)即可。
这里相当于就是用了2片缓冲区(固定大小),其实知道行数上限的话,用2个数组表示也一样。
最后发现,缓冲区一片就够了,这里和copy/copy_backward的原理是类似的,只要从后往前遍历的话就不会导致新元素覆盖了旧元素从而计算出错。
然后更进一步,杨辉三角形每一行是对称的。于是我们只需要取前半部分即可,对于奇数行取(n+1)/2个,对于偶数行取n/2个,按照C/C++中除法取整来看都是(n+1)/2个。
关键是,第2k+1行和第2k+2行的前半部分元素数量相同(比如第3行是1,2,第4行是1,3),而第2k+3行最后一个元素无法直接计算。其实仔细看看就会发现规律,由于对称性,第2k+3行最后一个元素是第2k+2行最后一个元素的2倍。
到这里就可以写代码了,但是写代码的时候直接按这个思路来代码会很丑,因为奇数行最后一个元素的计算方式和前面元素的计算方式不一致。一个优雅的写法是,每当从偶数行跳到奇数行时,元素数量增加,并且初始时在末尾添加一个元素,再批量计算。
比如第4行是1 3,那么第5行初始化后就是1 3 3。然后a[2] = a[1] + a[0]; a[1] = a[1] + a[0];来计算。
// 打印杨辉三角形的前n行
void printPascalTriangle(int n)
{
int maxrow = (n + ) / ;
vector<int> v(maxrow + );
v[] = ; // 哨兵节点
bool bOddRow = true; // 奇数行则为true
int num = ; // 需要计算的元素数量
for (int row = ; row <= n; row++)
{
if (bOddRow)
{
num++;
v[num] = v[num - ];
}
for (int i = num; i > ; i--)
v[i] += v[i - ]; for (int i = ; i <= num; i++) // 正向打印
cout << v[i] << " ";
if (!bOddRow) // 对于偶数行最后一个元素需要再打印一遍
cout << v[num] << " ";
for (int i = num - ; i >= ; i--) // 反向打印
cout << v[i] << " ";
cout << endl;
bOddRow = bOddRow ? false : true; // 行号+1后改变了奇偶性
}
}
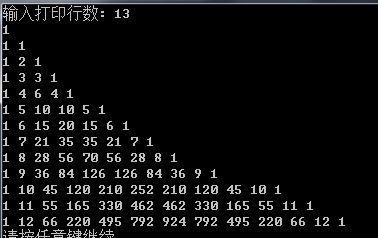
O(n)空间复杂度,打印杨辉三角形的前n行的更多相关文章
- 算法-利用队列实现逐行打印杨辉三角形的前n行
分别打印二项式(a+b)^n展开项的系数,在程序中利用了一个队列,在输出上一行系数时,将下一行的系数预先放入队列中.在各行系数间插入0. void YANGVI(int n){ Queue q(n+) ...
- ACM解题之快速输出杨辉三角形(前68行)
题意: 本题要求计算并输出杨辉三角形的前 68 行. Time Limit:1000MS Memory Limit:65536K 解题: 为了能在规定时间准确输出杨辉三角形的前68行,这里我用了精准的 ...
- 17.从键盘上输入一个正整数n,请按照以下五行杨辉三角形的显示方式, 输出杨辉三角形的前n行。请采用循环控制语句来实现。 (三角形腰上的数为1,其他位置的数为其上一行相邻两个数之和。) 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
17.从键盘上输入一个正整数n,请按照以下五行杨辉三角形的显示方式, 输出杨辉三角形的前n行.请采用循环控制语句来实现. (三角形腰上的数为1,其他位置的数为其上一行相邻两个数之和.) 1 1 1 1 ...
- 从键盘上输入一个正整数n,请按照以下五行杨辉三角形的显示方式, 输出杨辉三角形的前n行。请采用循环控制语句来实现。
Scanner sc=new Scanner(System.in); System.out.println("请输入一个正整数:"); int ss=sc.nextInt(); i ...
- grep命令打印前N行
想打印前5行,用head即可:grep xxx |head -n 5
- linux利用grep查看打印匹配的下几行或前后几行的命令
转自:http://www.itokit.com/2013/0308/74883.html linux系统中,利用grep打印匹配的上下几行 如果在只是想匹配模式的上下几行,grep可以实现. ...
- spark dataframe操作集锦(提取前几行,合并,入库等)
https://blog.csdn.net/sparkexpert/article/details/51042970 spark dataframe派生于RDD类,但是提供了非常强大的数据操作功能.当 ...
- linux grep打印匹配的上下几行
$grep -5 'parttern' inputfile //打印匹配行的前后5行 $grep -C 5 'parttern' inputfile //打印匹配行的前后5行 $grep -A 5 ' ...
- 1233: 输出杨辉三角前n行(Java)
WUSTOJ 1233: 输出杨辉三角前n行 题目 原题链接 Description 输出杨辉三角前n行. Input 输入一个数n(n <= 9) Output 输出杨辉三角前n行.(注意行末 ...
随机推荐
- git本地及远程分支回退
1. git本地版本回退 Git reset --hard commit_id(可用 git log –oneline 查看) 2. git远程版本回退 git push origin HEAD -- ...
- 萤石A1互联网报警盒子破解细节分析
攻击点分析: 萤石A1互联网报警盒子使用“全无线解决方案”,传感器的报警通过433.92MHz射频信号发送给报警主机,报警主机可以通过Wi-Fi联网,将报警上传萤石云端,云端会将信息推送到手机端的“ ...
- Python int操作
a = 1 # 1 print(a.bit_length()) #计算一个数字的二进制长度.没啥用
- IntelliJ IDEA使用(二):tomcat和jetty配置(转自:http://www.cnblogs.com/jenkinschan/p/6052948.html)
上一讲用idea创建了maven web项目,接下来我们把项目发布到tomcat和jetty运行,以便进一步地开发和调试 配置tomcat 第一.打开菜单栏 第二.点击设置按钮,添加应用服务器,选择t ...
- Hadoop streaming使用自定义python版本和第三方库
在使用Hadoop的过程中,遇到了自带python版本比较老的问题. 下面以python3.7为例,演示如何在hadoop上使用自定义的python版本以及第三方库. 1.在https://www.p ...
- C程序第四次作业
作业要求一 实践最简答的项目wordcount,必须完成其中的基本功能,若可以完成其他功能给予加分.完成后请将你的设计思路.主要代码写在本次作业博客里. 设计思路: 第一步:定义文件型指针变量fp,整 ...
- css3 制作平滑过度动画
-webkit-transition(属性渐变) -webkit-transition:CSS属性(none|all|属性) 持续时间 时间函数 延迟时间 CSS属性(transition-pr ...
- OK335xS canutils deal with compile error
/************************************************************************************** * OK335xS ca ...
- 【c++基础】判断是否到文件末尾-eof函数
前言 读取文件内容时,需要判断是否到文件末尾,此时用到eof函数. 函数定义 Check whether eofbit is set Returns true if theeofbiterror st ...
- 查看linux安装包的版本信息-TX2
前言 新到手一块TX2板子,想要检查系统是否安装某软件及其版本. 操作命令 Cuda8.:nvcc --version Opencv:pkg-config --modversion opencv G+ ...
