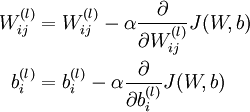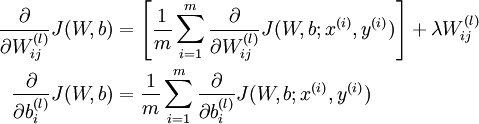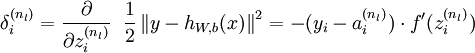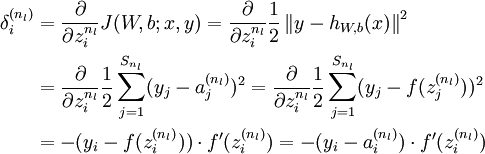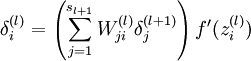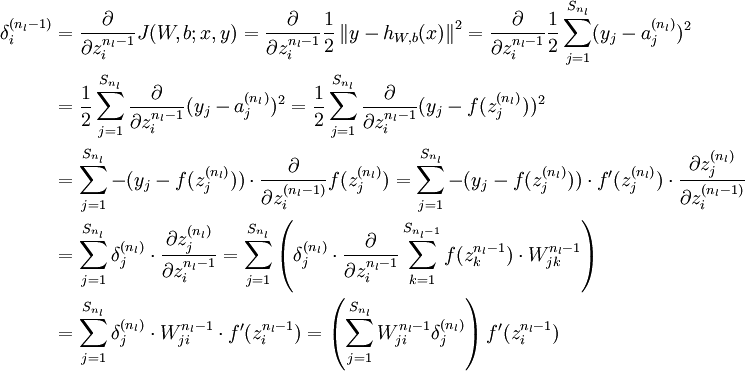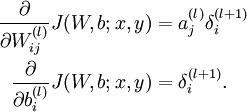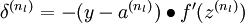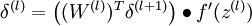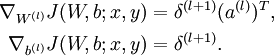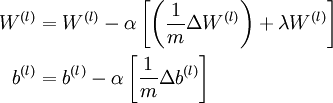反向传播算法 Backpropagation Algorithm
假设我们有一个固定样本集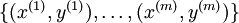 ,它包含
,它包含 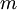 个样例。我们可以用批量梯度下降法来求解神经网络。具体来讲,对于单个样例(x,y),其代价函数为:
个样例。我们可以用批量梯度下降法来求解神经网络。具体来讲,对于单个样例(x,y),其代价函数为: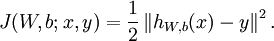 这是一个(二分之一的)方差代价函数。给定一个包含
这是一个(二分之一的)方差代价函数。给定一个包含 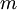 个样例的数据集,我们可以定义整体代价函数为:
个样例的数据集,我们可以定义整体代价函数为:
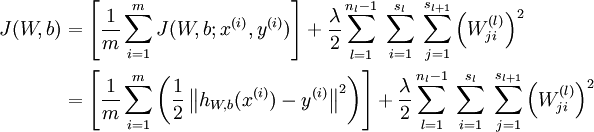
以上公式中的第一项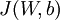 是一个均方差项。第二项是一个规则化项(也叫权重衰减项),其目的是减小权重的幅度,防止过度拟合。
是一个均方差项。第二项是一个规则化项(也叫权重衰减项),其目的是减小权重的幅度,防止过度拟合。
[注:通常权重衰减的计算并不使用偏置项 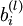 ,比如我们在
,比如我们在 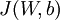 的定义中就没有使用。一般来说,将偏置项包含在权重衰减项中只会对最终的神经网络产生很小的影响。在贝叶斯规则化方法中,我们将高斯先验概率引入到参数中计算MAP(极大后验)估计(而不是极大似然估计)。]
的定义中就没有使用。一般来说,将偏置项包含在权重衰减项中只会对最终的神经网络产生很小的影响。在贝叶斯规则化方法中,我们将高斯先验概率引入到参数中计算MAP(极大后验)估计(而不是极大似然估计)。]
权重衰减参数 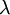 用于控制公式中两项的相对重要性。在此重申一下这两个复杂函数的含义:
用于控制公式中两项的相对重要性。在此重申一下这两个复杂函数的含义: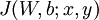 是针对单个样例计算得到的方差代价函数;
是针对单个样例计算得到的方差代价函数;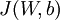 是整体样本代价函数,它包含权重衰减项。
是整体样本代价函数,它包含权重衰减项。
以上的代价函数经常被用于分类和回归问题,在分类问题中,我们用y=0或y=1,来代表两种类型的标签(回想一下,这是因为sigmoid激活函数的值域为[0,1];如果我们使用双曲正切型激活函数,那么应该选用-1和+1作为标签)。对于回归问题,我们首选要变换输出值域(也就是y)以保证其范围为[0,1](同样地,如果我们使用双曲正切型激活函数,要使用输出值域为[-1,1])。
我们的目标是针对W和b来求其函数J(W,b)的最小值。为了求解神经网络,我们需要将每一个参数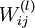 和
和 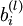 初始化为一个很小的,接近零的随机值(比如说,使用正态分布
初始化为一个很小的,接近零的随机值(比如说,使用正态分布 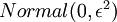 生成的随机值,其中
生成的随机值,其中 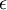 设置为
设置为 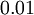 ),之后对目标函数使用诸如梯度批量梯度下降法的最优化算法。因为
),之后对目标函数使用诸如梯度批量梯度下降法的最优化算法。因为 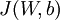 是一个非凸函数,梯度下降法很可能会收敛到局部最优解;但是实际应用中,梯度下降法通常能够得到令人满意的结果,最后,需要再次强调的是,要将参数进行随机初始化,而不是全部置为0.如果所有参数都用相同的值作为初值,那么所有隐藏层单元最终会得到与输入值有关的,相同的函数(也就是说,对于所有
是一个非凸函数,梯度下降法很可能会收敛到局部最优解;但是实际应用中,梯度下降法通常能够得到令人满意的结果,最后,需要再次强调的是,要将参数进行随机初始化,而不是全部置为0.如果所有参数都用相同的值作为初值,那么所有隐藏层单元最终会得到与输入值有关的,相同的函数(也就是说,对于所有  ,
,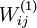 都会取相同的值,那么对于任何输入
都会取相同的值,那么对于任何输入  都会有:
都会有: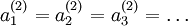 )。随机初始化的目的是使对称失效。
)。随机初始化的目的是使对称失效。
梯度下降法中每一次迭代都按照如下公式对参数W和b进行更新:
其中 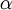 是学习速率。其中关键步骤是计算偏导数。我们现在来讲一下反向传播算法,它是计算偏导数的一种有效方法。
是学习速率。其中关键步骤是计算偏导数。我们现在来讲一下反向传播算法,它是计算偏导数的一种有效方法。
我们首先讲一下如何使用反向传播算法来计算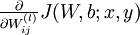 和
和 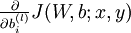 ,这两项是单个样例
,这两项是单个样例 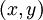 的代价函数
的代价函数 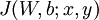 的偏导数。
的偏导数。
一旦我们求出该偏导数,就可以推导出整体代价函数 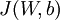 的偏导数:
的偏导数:
以上两行公式稍有不同,第一行比第二行多出一项,是因为权重衰减是作用于 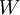 而不是
而不是 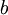 。
。
反向传播算法的思路如下:给定一个样例(x,y),我们首先进行“前向传导”运算,计算出网络中所有激活值(我们用 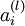 表示第
表示第  层第
层第  单元的激活值(输出值)。)包括
单元的激活值(输出值)。)包括 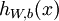 的输出值(
的输出值(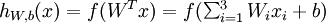 )。之后,针对第针对第
)。之后,针对第针对第  层的每一个节点
层的每一个节点  ,我们计算出其“残差”
,我们计算出其“残差” 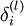 ,,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为
,,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为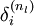 (第
(第 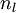 层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第
层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第 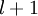 层节点)残差的加权平均值计算
层节点)残差的加权平均值计算 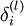 ,这些节点以
,这些节点以 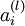 作为输入。下面将给出反向传导算法的细节:
作为输入。下面将给出反向传导算法的细节:
1、进行前馈传导计算,利用前向传导公式,得到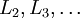 直到输出层
直到输出层 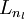 的激 活值。
的激 活值。
2、对于第 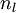 层(输出层)的每个输出单元
层(输出层)的每个输出单元  ,我们根据以下公式计算残差:
,我们根据以下公式计算残差:
[译者注:
]
3、对 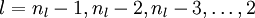 的各个层,第
的各个层,第  层的第
层的第  个节点的残差计算方法如下:
个节点的残差计算方法如下:
{译者注:
将上式中的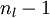 与
与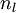 的关系替换为
的关系替换为 与
与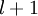 的关系,就可以得到:
的关系,就可以得到:
以上逐次从后向前求导的过程即为“反向传导”的本意所在。]
4、计算我们需要的偏导数,计算方法如下:
最后,我们用矩阵-向量表示法重写以上算法。我们使用“ ” 表示向量乘积运算符(在Matlab或Octave里用“.*”表示,也称作阿达马乘积)。若
” 表示向量乘积运算符(在Matlab或Octave里用“.*”表示,也称作阿达马乘积)。若 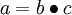 ,则
,则 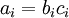 。在上一个教程中我们扩展了
。在上一个教程中我们扩展了 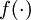 的定义,使其包含向量运算,这里我们也对偏导数
的定义,使其包含向量运算,这里我们也对偏导数 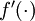 也做了同样的处理(于是又有
也做了同样的处理(于是又有 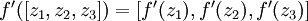 )。
)。
那么,反向传播算法可以表示为以下几个步骤:
1、进行前馈传导计算,利用前向传导公式,得到 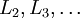 直到输出层
直到输出层 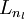 的激活值。
的激活值。
2、对输出层(第 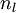 层),计算残差:
层),计算残差:
3、对于 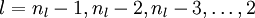 的各层,计算:
的各层,计算:
4、计算最终需要的偏导数值:
实现中应注意:在以上的第2步和第3步中,我们需要为每一个  值计算其
值计算其 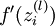 。假设
。假设 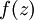 是sigmoid函数,并且我们已经在前向传导运算中得到了
是sigmoid函数,并且我们已经在前向传导运算中得到了 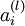 。那么,使用我们早先推导出的
。那么,使用我们早先推导出的 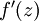 表达式,就可以计算得到
表达式,就可以计算得到 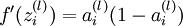 。
。
最后,我们将对梯度下降算法做个全面总结。在下面的伪代码中,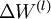 是一个与矩阵
是一个与矩阵 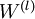 维度相同的矩阵,
维度相同的矩阵,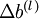 是一个与
是一个与 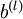 维度相同的向量。下面,我们实现爱你批量梯度下降法中的一次迭代:
维度相同的向量。下面,我们实现爱你批量梯度下降法中的一次迭代:
- 对于所有
 ,令
,令 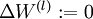 ,
, 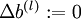 (设置为全零矩阵或全零向量)
(设置为全零矩阵或全零向量) - 对于
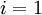 到
到 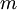 ,更新权重参数:
,更新权重参数:
- 使用反向传播算法计算
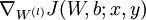 和
和 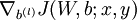 。
。 - 计算
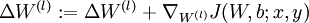 。
。 - 计算
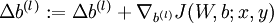 。
。
- 使用反向传播算法计算
3、更新权重参数:
现在,我们可以重复梯度下降法的迭代步骤来减小代价函数 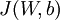 的值,进而求解我们的神经网络。
的值,进而求解我们的神经网络。
中英文对照:
反向传播算法 Backpropagation Algorithm
(批量)梯度下降法(batch)gradient descent
(整体)代价函数 (overall)cost function
方差 squared-error
均方差 average sum-of-squares error
规则化项 regularization term
权重衰减 weight decay
偏置项 bias terms
贝叶斯规则化方法 Bayesian regularization method
高斯先验概率 Gaussian piror
极大后验估计 MAP
极大似然估计 maximum likelihood estimation
激活函数 activation function
双曲正切函数 tanh function
非凸函数 non-convex function
隐藏层单元 hidden (layer) units
对称失效 symmetry breaking
学习速率 learning rate
前向传导 forward pass
假设值 hypothesis
残差 error term
加权平均值 weighted average
前馈传导 feedforward pass
阿达马乘积 Hadamard product
前向传播 forward propagation
反向传播算法 Backpropagation Algorithm的更多相关文章
- [2] TensorFlow 向前传播算法(forward-propagation)与反向传播算法(back-propagation)
TensorFlow Playground http://playground.tensorflow.org 帮助更好的理解,游乐场Playground可以实现可视化训练过程的工具 TensorFlo ...
- 一文弄懂神经网络中的反向传播法(Backpropagation algorithm)
最近在看深度学习的东西,一开始看的吴恩达的UFLDL教程,有中文版就直接看了,后来发现有些地方总是不是很明确,又去看英文版,然后又找了些资料看,才发现,中文版的译者在翻译的时候会对省略的公式推导过程进 ...
- 神经网络(9)--如何求参数: backpropagation algorithm(反向传播算法)
Backpropagation algorithm(反向传播算法) Θij(l) is a real number. Forward propagation 上图是给出一个training examp ...
- 深度学习课程笔记(三)Backpropagation 反向传播算法
深度学习课程笔记(三)Backpropagation 反向传播算法 2017.10.06 材料来自:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS1 ...
- 神经网络(NN)+反向传播算法(Backpropagation/BP)+交叉熵+softmax原理分析
神经网络如何利用反向传播算法进行参数更新,加入交叉熵和softmax又会如何变化? 其中的数学原理分析:请点击这里.
- 循环神经网络(RNN)模型与前向反向传播算法
在前面我们讲到了DNN,以及DNN的特例CNN的模型和前向反向传播算法,这些算法都是前向反馈的,模型的输出和模型本身没有关联关系.今天我们就讨论另一类输出和模型间有反馈的神经网络:循环神经网络(Rec ...
- 机器学习 —— 基础整理(七)前馈神经网络的BP反向传播算法步骤整理
这里把按 [1] 推导的BP算法(Backpropagation)步骤整理一下.突然想整理这个的原因是知乎上看到了一个帅呆了的求矩阵微分的方法(也就是 [2]),不得不感叹作者的功力.[1] 中直接使 ...
- 【机器学习】反向传播算法 BP
知识回顾 1:首先引入一些便于稍后讨论的新标记方法: 假设神经网络的训练样本有m个,每个包含一组输入x和一组输出信号y,L表示神经网络的层数,S表示每层输入的神经元的个数,SL代表最后一层中处理的单元 ...
- 前向传播算法(Forward propagation)与反向传播算法(Back propagation)
虽然学深度学习有一段时间了,但是对于一些算法的具体实现还是模糊不清,用了很久也不是很了解.因此特意先对深度学习中的相关基础概念做一下总结.先看看前向传播算法(Forward propagation)与 ...
随机推荐
- Android零碎知识点
1.android:foreground="?attr/selectableItemBackground" ###设置水波纹效果 2.android:contentDescri ...
- 北京Uber优步司机奖励政策(3月21日)
滴快车单单2.5倍,注册地址:http://www.udache.com/ 如何注册Uber司机(全国版最新最详细注册流程)/月入2万/不用抢单:http://www.cnblogs.com/mfry ...
- CF 480 E. Parking Lot
CF 480 E. Parking Lot http://codeforces.com/contest/480/problem/E 题意: 给一个n*m的01矩阵,每次可以将一个0修改为1,求最大全0 ...
- fastDFS 分布式文件系统应用
环境准备 使用的系统软件 名称 说明 centos 7.x libfatscommon FastDFS分离出的一些公用函数包 FastDFS FastDFS本体 fastdfs-nginx-modul ...
- LWM2M简介-学习记录
1. Lightweight M2M 基础,谁搞出来的 OMA是一家国际组织,因为物联网的兴起, OMA在传统的OMA-DM协议基础之上,提出了LWM2M协议.这个协议基于COAP协议,COAP协议基 ...
- 「国庆训练」Kingdom of Obsession(HDU-5943)
题意 给定\(s,n\),把\(s+1,s+2,...,s+n\)这\(n\)个数填到\(1,2,...,n\)里,要求\(x\)只能填到\(x\)的因子的位置(即题目中\(x\%y=0\)那么x才能 ...
- Nginx与Ribbon的区别
服务器端负载均衡 Nginx Nginx 基于C语言,快速,性能高5w/s. Redis 5w/s,RibbatMQ 1.2w/s ApacheActiveMQ 0.6w/s 业务系统,kafka 2 ...
- VMWare Workstation新装CentOS 7无法联网解决办法
按照这位博主的方法成功解决:http://blog.csdn.net/deniro_li/article/details/54632949
- 承压计算:模拟+double
标题:承压计算 X星球的高科技实验室中整齐地堆放着某批珍贵金属原料. 每块金属原料的外形.尺寸完全一致,但重量不同.金属材料被严格地堆放成金字塔形. 7 ...
- 1.EOS源码编译运行
目前网络上都是针对老版EOS2.0源码编译的文章,我在mac上参考这些文章编译,最后发现根本就不对,最新版本只需一条命令(./eosio_build.sh,依赖库会自动安装的)即可.我根据这些文章手动 ...