CodeForces 316D3 PE Lesson

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Smart Beaver decided to be not only smart, but also a healthy beaver! And so he began to attend physical education classes at school X. In this school, physical education has a very creative teacher. One of his favorite warm-up exercises is throwing balls. Students line up. Each one gets a single ball in the beginning. The balls are numbered from 1 to n (by the demand of the inventory commission).

Figure 1. The initial position for n = 5.

After receiving the balls the students perform the warm-up exercise. The exercise takes place in a few throws. For each throw the teacher chooses any two arbitrary different students who will participate in it. The selected students throw their balls to each other. Thus, after each throw the students remain in their positions, and the two balls are swapped.

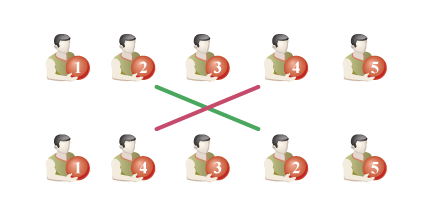Figure 2. The example of a throw.

In this case there was a throw between the students, who were holding the 2-nd and the 4-th balls. Since the warm-up has many exercises, each of them can only continue for little time. Therefore, for each student we know the maximum number of throws he can participate in. For this lessons maximum number of throws will be 1 or 2.

Note that after all phases of the considered exercise any ball can end up with any student. Smart Beaver decided to formalize it and introduced the concept of the "ball order". The ball order is a sequence of n numbers that correspond to the order of balls in the line. The first number will match the number of the ball of the first from the left student in the line, the second number will match the ball of the second student, and so on. For example, in figure 2 the order of the balls was (1, 2, 3, 4, 5), and after the throw it was (1, 4, 3, 2, 5). Smart beaver knows the number of students and for each student he knows the maximum number of throws in which he can participate. And now he is wondering: what is the number of distinct ways of ball orders by the end of the exercise.

Input

The first line contains a single number n — the number of students in the line and the number of balls. The next line contains exactly n space-separated integers. Each number corresponds to a student in the line (the i-th number corresponds to the i-th from the left student in the line) and shows the number of throws he can participate in.

The input limits for scoring 30 points are (subproblem D1):

• 1 ≤ n ≤ 10.

The input limits for scoring 70 points are (subproblems D1+D2):

• 1 ≤ n ≤ 500.

The input limits for scoring 100 points are (subproblems D1+D2+D3):

• 1 ≤ n ≤ 1000000.

Output

The output should contain a single integer — the number of variants of ball orders after the warm up exercise is complete. As the number can be rather large, print it modulo 1000000007 (10⁹ + 7).

Examples

Input

5
1 2 2 1 2

Output

120

Input

8
1 2 2 1 2 1 1 2

Output

16800

数学问题 脑洞题 组合数

有的人可以交换两次，有的人可以交换一次。

脑洞一下可以注意到只要交换的方案不同，最终的排列就不同。

如果所有人都只能交换一次，设f[i]表示有i个只能交换一次的人的交换方案数。

f[i]=f[i-1]+(i-1)*f[i-2]  （自己跟自己玩，或者找一个人换）

考虑能交换两次的人，若这类人有a个，那么他们可选择的交换方案共有$C(n,a)*A(a,a)=n*(n-1)*(n-2)*...*(n-a+1)$种，交换完后正好剩下n-a个只能交换一次的，所以再乘上f[n-a]即可

具体考虑方法的话……假设x和y交换，如果x剩2，y剩1，那么剩下一个1一个0；如果x剩2，y剩2，换了以后剩下两个1，但y还是要当做能换两次的，去考虑和其他某个人交换，这样的交换关系形成一条链（这条链的起始点是一个原本只能换一次的人），于是连续的一串2会消到只剩下一个1

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #define LL long long
 using namespace std;
 const int mod=1e9+;
 const int mxn=;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n;
 int a[mxn];
 int f[mxn];
 int main(){
 //    freopen("in.txt","r",stdin);
     int i,j,cnt=;
     n=read();
     for(i=;i<=n;i++){a[i]=read();if(a[i]==)cnt++;}
     f[]=;f[]=;f[]=;
     for(i=;i<=cnt;i++)f[i]=((LL)f[i-]+(LL)f[i-]*(i-)%mod)%mod;
     for(i=n;i>cnt;i--)f[cnt]=(LL)f[cnt]*i%mod;
     printf("%d\n",f[cnt]);
     return ;
 }