算法-最通俗易懂的KMP算法详解

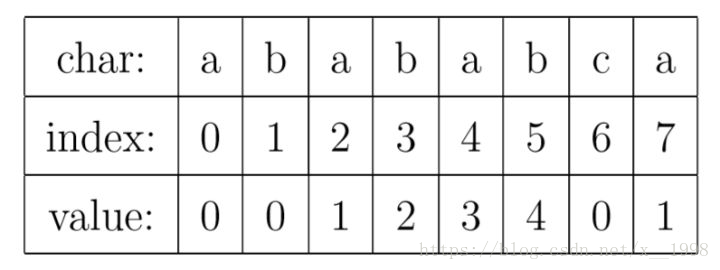
有些算法，适合从它产生的动机，如何设计与解决问题这样正向地去介绍。但KMP算法真的不适合这样去学。最好的办法是先搞清楚它所用的数据结构是什么，再搞清楚怎么用，最后为什么的问题就会有恍然大悟的感觉。我试着从这个思路再介绍一下。大家只需要记住一点，PMT是什么东西。然后自己临时推这个算法也是能推出来的，完全不需要死记硬背。KMP算法的核心，是一个被称为部分匹配表(Partial Match Table)的数组。我觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后，仍然搞不懂PMT中的值代表了什么意思。这里我们抛开所有的枝枝蔓蔓，先来解释一下这个数据到底是什么。对于字符串“abababca”，它的PMT如下表所示：

就像例子中所示的，如果待匹配的模式字符串有8个字符，那么PMT就会有8个值。

我先解释一下字符串的前缀和后缀。如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。同样可以定义后缀A=SB， 其中S是任意的非空字符串，那就称B为A的后缀，例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。要注意的是，字符串本身并不是自己的后缀。

有了这个定义，就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长 度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。再比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。

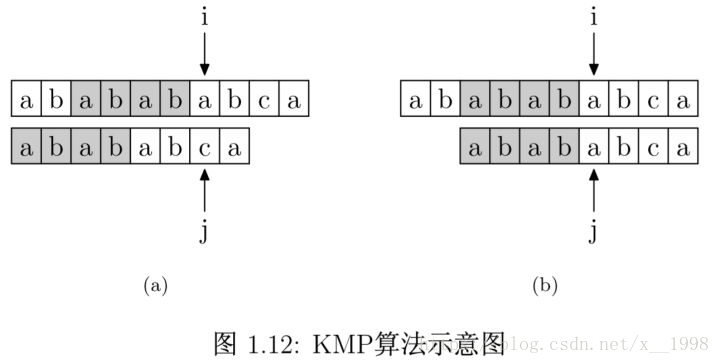
好了，解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么。如图 1.12 所示，要在主字符串"ababababca"中查找模式字符串"abababca"。如果在 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。而我们上面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是”ababab”，其前缀集合与后缀集合的交集的最长元素为”abab”， 长度为4。所以就可以断言，主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持i指针不动，然后将j指针指向模式字符串的PMT[j −1]位即可。

简言之，以图中的例子来说，在 i 处失配，那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。

有了上面的思路，我们就可以使用PMT加速字符串的查找了。我们看到如果是在 j 位 失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用PMT数组，而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是，在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。在本节的例子中，next数组如下表所示。

 

1.  
   int KMP(char * t, char * p)
2.  
   {
3.  
   int i = 0;
4.  
   int j = 0;
5.  
    
6.  
   while (i < strlen(t) && j < strlen(p))
7.  
   {
8.  
   if (j == -1 || t[i] == p[j])
9.  
   {
10.  
    i++;
11.  
    j++;
12.  
    }
13.  
    else
14.  
    j = next[j];
15.  
    }
16.  
     
17.  
    if (j == strlen(p))
18.  
    return i - j;
19.  
    else
20.  
    return -1;
21.  
    }

好了，讲到这里，其实KMP算法的主体就已经讲解完了。你会发现，其实KMP算法的动机是很简单的，解决的方案也很简单。远没有很多教材和算法书里所讲的那么乱七八糟，只要搞明白了PMT的意义，其实整个算法都迎刃而解。

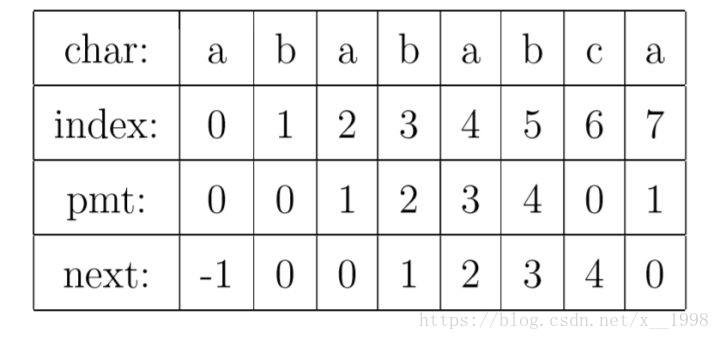
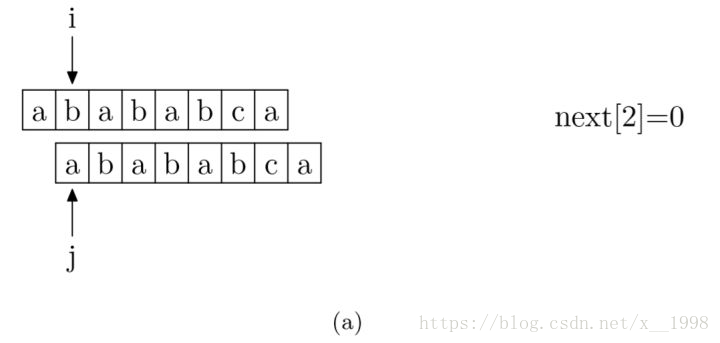
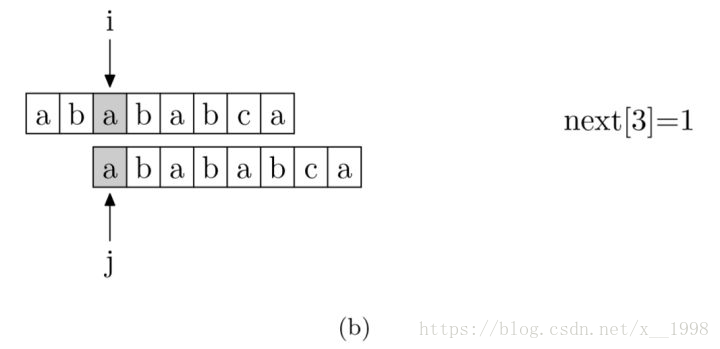
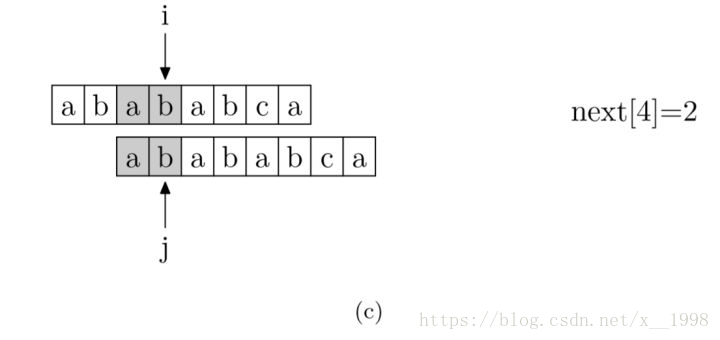
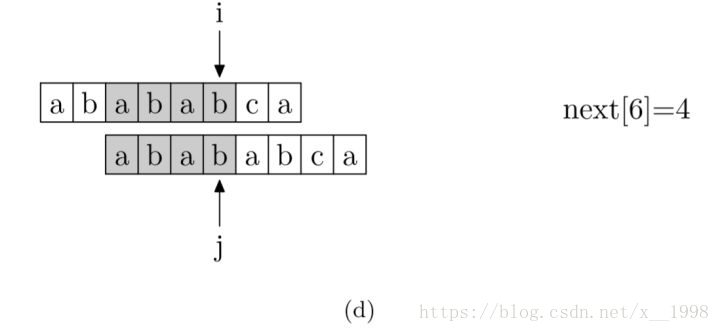
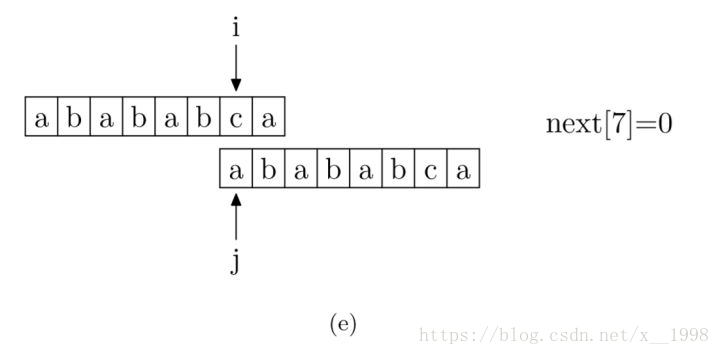
现在，我们再看一下如何编程快速求得next数组。其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。

具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前位置的next值。如下图所示。

求next数组值的程序如下所示：

1.  
   void getNext(char * p, int * next)
2.  
   {
3.  
   next[0] = -1;
4.  
   int i = 0, j = -1;
5.  
    
6.  
   while (i < strlen(p))
7.  
   {
8.  
   if (j == -1 || p[i] == p[j])
9.  
   {
10.  
    ++i;
11.  
    ++j;
12.  
    next[i] = j;
13.  
    }
14.  
    else
15.  
    j = next[j];
16.  
    }
17.  
    }

作者：海纳
链接：https://www.zhihu.com/question/21923021/answer/281346746
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。