Unty中通过镜像优化HDRI全景图体积

全景图即HDRI贴图，可以代替6面cubemap，传统3D软件运用较为广泛。一般反射探针，天空盒等都会用到。

但是体积过大是个问题，特别是移动端会对包体大小进行控制，虽说可以通过球面贴图替换掉部分环境类贴图，但适用范围依然有限。

这里通过镜像的方式来做贴图大小的优化，可将贴图优化到原先的一半大小。

原图如下(网络收集)：

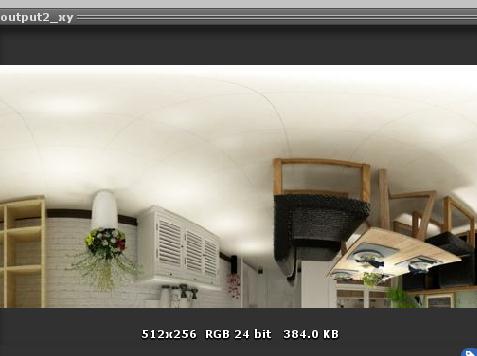
最终效果(左右上下镜像)：

github上有一些Equirectangular map的转换函数，类似球面坐标，直接拿来主义了。

参考:

https://github.com/tolotratlt/UnityPhotosphericView

https://github.com/Mapiarz/CubemapToEquirectangular

经过测试是可以x,y轴镜像的，首先需裁剪原始HDRI图片。直接用Texture2D的Resize裁一下即可。ConvShader就是两个镜像函数的转换shader，不贴出来了

Material mat = new Material(Shader.Find("Hidden/ConvShader"));
var rt = RenderTexture.GetTemporary(new RenderTextureDescriptor(tex.width, tex.height, RenderTextureFormat.ARGB32));
Graphics.Blit(tex, rt, mat);
 
var instanceTex = Instantiate(tex);
 
instanceTex.Resize(instanceTex.width, instanceTex.height / );
instanceTex.ReadPixels(new Rect(, , instanceTex.width, instanceTex.height), , );
instanceTex.Apply();
...

主要是转换全景图的两个函数，参考了github上的内容，顺带把常量改成了内置的UNITY_PI。

float3 UvToDir(float2 uv)
{
    uv *= float2(UNITY_TWO_PI, UNITY_PI);
 
    float theta = uv.y;
    float phi = uv.x;
    float3 dir = float3(, , );
 
    dir.x = sin(phi) * sin(theta) * -;
    dir.y = cos(theta) * -;
    dir.z = cos(phi) * sin(theta) * -;
 
    return dir;
}
 
float2 DirToUV(float3 a_coords)
{
    float3 a_coords_n = normalize(a_coords);
 
    float lon = atan2(a_coords_n.z, a_coords_n.x);
    float lat = acos(a_coords_n.y);
    float2 sphereCoords = float2(lon, lat) * (1.0 / UNITY_PI);
    return float2( - (sphereCoords.x * 0.5 - 0.5),  - sphereCoords.y); //must flip x
}

转换之后就是在显示部分做修改，通过传入一个方向矢量来返回全景图的UV，并在其内部做镜像图片的修复

需注意输出x分量并非0-1区间，而是0-2，估计由于全景图宽高2:1导致的，这里简单修复了下。

而y轴接缝较为明显，通过手动调节误差。压缩，关闭mipmap等。接缝问题会得到缓解。

float2 DirToUV(float3 a_coords)
{
    float3 a_coords_n = normalize(a_coords);
 
    float lon = atan2(a_coords_n.z, a_coords_n.x);
    float lat = acos(a_coords_n.y);
    float2 sphereCoords = float2(lon, lat) * (1.0 / UNITY_PI);
    float2 uv = float2( - (sphereCoords.x * 0.5 - 0.5),  - sphereCoords.y);
 
    //----------------------------
    uv.x -= ;
 
    if (uv.x > 0.5)
        uv.x = 0.5 - (uv.x - 0.5);
 
    uv.x *= ;
    //----------------------------Mirror X.
 
    //----------------------------
    uv.y *= 1.999;
 
    if (uv.y < )
        uv.y *= -0.97;
    else
        uv.y *= 1.03;
    //----------------------------Mirror Y.
 
    return uv;
}

基本如上，另外很多情况下需要Cubemap转HDRI全景图，可直接参考维基百科上的Cubemaping映射函数：

https://en.wikipedia.org/wiki/Cube_mapping