OR in Matrix

OR in Matrix

Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

 where 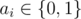 is equal to 1 if some a_i = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as A_ij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

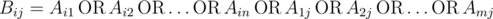(B_ij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print m rows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

Sample Input

Input

2 2
1 0
0 0

Output

NO

Input

2 3
1 1 1
1 1 1

Output

YES
1 1 1
1 1 1

Input

2 3
0 1 0
1 1 1

Output

YES
0 0 0
0 1 0

/*
题意：定义一个异或，a1^a2...^an如果有一个ai=1那么值为1，否则为零，给出你一个矩阵B,是由矩阵A得来的，Bij等于A的i行元素
    异或j列元素。给出你矩阵B问你是否有这样的矩阵A

初步思路：将矩阵初始化为1，然后先按照矩阵B中有零的元素，将对应A矩阵中的元素设置成零，然后在反过来验证B矩阵
*/
#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[][];
int b[][];
int main(){
    // freopen("in.txt","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++){
        for(int j=;j<=m;j++){
            scanf("%d",&b[i][j]);
            a[i][j]=;
        }
    }
    //按照B矩阵进行置0
    for(int i=;i<=n;i++){
        for(int j=;j<=m;j++){
            if(b[i][j]==){
                for(int k=;k<=m;k++)
                    a[i][k]=;
                for(int k=;k<=n;k++)
                    a[k][j]=;
            }
        }
    }
    //验证然后按照1的位置验证B矩阵
    bool f=false;
    for(int i=;i<=n;i++){
        for(int j=;j<=m;j++){
            if(b[i][j]==){
                bool flag=false;
                for(int k=;k<=n;k++){
                    if(a[i][k]==){
                        flag=true;
                        break;
                    }
                }
                if(flag==false)
                for(int k=;k<=m;k++){
                    if(a[k][j]==){
                        flag=true;
                        break;
                    }
                }
                if(flag==false){
                    f=true;
                    break;
                }
            }
        }
    }
    if(f){
        puts("NO");
    }else{
        puts("YES");
        for(int i=;i<=n;i++){
            for(int j=;j<=m;j++){
                printf(j==?"%d":" %d",a[i][j]);
            }
            printf("\n");
        }
    }
    return ;
}