code force 403B.B. The Meeting Place Cannot Be Changed

B. The Meeting Place Cannot Be Changed

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.

At some points on the road there are n friends, and i-th of them is standing at the point xi meters and can move with any speed no greater than vi meters per second in any of the two directions along the road: south or north.

You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.

Input

The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.

The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) — the current coordinates of the friends, in meters.

The third line contains n integers v1, v2, ..., vn (1 ≤ vi ≤ 109) — the maximum speeds of the friends, in meters per second.

Output

Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.

Your answer will be considered correct, if its absolute or relative error isn't greater than 10 - 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 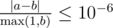 holds.

Examples

input

3
7 1 3
1 2 1

output

2.000000000000

input

4
5 10 3 2
2 3 2 4

output

1.400000000000

Note

In the first sample, all friends can gather at the point 5 within 2 seconds. In order to achieve this, the first friend should go south all the time at his maximum speed, while the second and the third friends should go north at their maximum speeds.

/*
题意：有n个朋友在一条南北方向的坐标轴上，n个朋友每人都有自己的最大速度，现在让你求出让n个朋友在
    某点汇合的最小时间

初步思路：二分，二分判断的条件就是这些点，在时间t内向南走的最大距离，和向北走的最小距离能不能相
    遇，如果能相遇的话，那么这个时间就可以
*/

#include<bits/stdc++.h>
using namespace std;
long long n,i,x[],v[];
long double l,r,t,eps,mx,mn;
int main()
{
    // freopen("in.txt","r",stdin);
    cin>>n;
    for (i=;i<=n;i++) cin>>x[i];
    for (i=;i<=n;i++) cin>>v[i];
    r=1e9; eps=1e-;
    while(r-l>eps)
    {
        t=(r+l)/2.0;
        mx=x[]-t*v[];
        mn=x[]+t*v[];
        for(i=;i<=n;i++)
        {
            if (mx<x[i]-t*v[i])//向南走能到达的最大的范围
                mx=x[i]-t*v[i];
            if (mn>x[i]+t*v[i])//向北走能到达的最小的范围
                mn=x[i]+t*v[i];
        }
        // cout<<mx<<" "<<mn<<endl;
        if (mx<=mn) //如果向南走的距离小于等于向北走的距离，就缩小二分的边界
            r=t;
        else //否则就扩大二分的边界
            l=t;
    }
    cout<<fixed<<l;
}