magic矩阵
魔方矩阵
魔方矩阵是有相同的行数和列数,并在每行每列、对角线上的和都相等。你能构造任何大小(除了2x2)的魔方矩阵。
1.历史
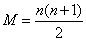
2.魔方构造
N 为奇数时
N为4的倍数时
N 为其它偶数时
3.算法设计
4.魔方函数
>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
magic矩阵的更多相关文章
- magic矩阵 分类: 数学 2015-07-31 22:56 2人阅读 评论(0) 收藏
魔方矩阵 魔方矩阵是有相同的行数和列数,并在每行每列.对角线上的和都相等.你能构造任何大小(除了2x2)的魔方矩阵. 1.历史 魔方又称幻方.纵横图.九宫图,最早记录于我国古代的洛书.据说 ...
- matlab基础教程——根据Andrew Ng的machine learning整理
matlab基础教程--根据Andrew Ng的machine learning整理 基本运算 算数运算 逻辑运算 格式化输出 小数位全局修改 向量和矩阵运算 矩阵操作 申明一个矩阵或向量 快速建立一 ...
- 【5.1送礼】国内第一部Matlab和C#.Net混合编程视频教程【免费】
本博客所有文章分类的总目录:[总目录]本博客博文总目录-实时更新 Matlab和C#混合编程文章目录 :[目录]Matlab和C#混合编程文章目录 上一次写博客很久了 ...
- MATLAB命令大全
一.常用对象操作:除了一般windows窗口的常用功能键外.1.!dir 可以查看当前工作目录的文件. !dir& 可以在dos状态下查看.2.who 可以查看当前工作空间变量名, whos ...
- [转] MATLAB快捷键
原文地址:MATLAB快捷键大全 (转载)作者:掷地有声 一.索引混排版 备注:删除了如F1(帮助)等类型的常见快捷命令 SHIFT+DELETE永久删除 DELETE删除 ALT+ENTER属性 A ...
- MATLAB命令大全+注释小结
一.常用对象操作:除了一般windows窗口的常用功能键外.1.!dir 可以查看当前工作目录的文件. !dir& 可以在dos状态下查看.2.who 可以查看当前工作空间变量名, ...
- 入坑MATLAB必会的吐血总结
本渣想回过头来整理一下MATLAB的一些基本的知识(很多东西比较琐碎,应该系统的梳理梳理),下文中没有提到的,自己用help查即可. 此文用来存个档,便于回顾. 由于matlab各版本部分语法存在差异 ...
- Matlab常用函数集锦
ndims(A)返回A的维数size(A)返回A各个维的最大元素个数length(A)返回max(size(A))[m,n]=size(A)如果A是二维数组,返回行数和列数nnz(A)返回A中非0元素 ...
- octave基本指令3
octave基本指令3 数据运算 >> a = [1 2; 3 4; 5 6]; >> b = [11 12; 13 14; 15 16]; >> c = [1 1 ...
随机推荐
- MATLAB 函数
MATLAB函数大全 1.常见 http://wenku.baidu.com/link?url=tPpwD7Ox_1sG-SQv_XdYszBAPY9LX_Zb_dde_5JeOiu7RwN_i14X ...
- 进制转换器(十进制转n进制)
#include<stdio.h> #include<stdlib.h> #define MAXSIZE 100 /*链栈类型定义*/ typedef struct node ...
- 跨域SSO的实现
翻译自CodeProject网站ASP.NET9月份最佳文章:Single Sign On (SSO) for cross-domain ASP.NET applications. 翻译不妥之处还望大 ...
- 使用icon替换你的网页图标(转)
第一次使用 Font Awesome 发现相当的爽呀!它的图标很全,能够帮你节约时间去找图片.下面就来一起学习吧: 1: 去官方网站下载解压 http://fontawesome.io/ 2: 解压后 ...
- 网络安全之PHP安全编程建议
要提供互联网服务,当你在开发代码的时候必须时刻保持安全意识.可能大部分 PHP 脚本都对安全问题都不在意,这很大程度上是因为有大量的 无经验程序员 在使用这门语言.但是,没有理由让你因为对你的代码的不 ...
- GPIO的8种工作模式
1.浮空输入GPIO_IN_FLOATING ——浮空输入,可以做KEY识别,RX1 2.带上拉输入GPIO_IPU——IO内部上拉电阻输入 3.带下拉输入GPIO_IPD——IO内部下拉电阻输入 4 ...
- ACM - 动态规划专题 题目整理
CodeForces 429B Working out 预处理出从四个顶点到某个位置的最大权值,再枚举相遇点,相遇的时候只有两种情况,取最优解即可. #include<iostream> ...
- iOS 版本号Version和Build的区别
一个version,一个build,都是设置版本的地方,有什么区别呢? 在ios中(Android等工程中也一样),有两种version,一种是 CFBundleVersion ("Bund ...
- python黑帽子源码
https://www.nostarch.com/download/BHP-Code.zip https://yunpan.cn/cPvLPWMTdWJRu 访问密码 4243
- (spring-第11回【IoC基础篇】)BeanWrapper--实例化Bean的第四大利器
重复是理解和记忆的最好方法.在讲实例化Bean的每个步骤之前,我都会先复习一下Bean实例化的整个过程: 结合图片我们回顾一下具体的过程: ResourceLoader加载配置信息, 由BeanDef ...
