Ackerman函数

Ackerman函数在许多讲解递归的书中都提到，但似乎又对解题没有太大的意义，暂时不知道了。不过这个东西，是一个数学知识点，暂时收藏于此吧。

查了一下维基百科和百度百科，表面上两个定义不一样，仔细推敲其实是一样的。（维基百科里面A（m，n）和百度百科里面A（n，m）当中的参数n、m代表含义是一样的，只是它们两个递归函数的参数的顺序写的不一样而已。）

先看Fibonacci数列

Fibonacci数列是一个非常重要，应用非常广的知识点，其递归定义如下：

（百度百科：http://baike.baidu.com/link?url=hSbCp3OLCl79y1H_fDWugAniyMFuEK7IlB2KB--g2oLAMkcWvv_3wkJRjClkq2cg）

递推公式

斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

如果设F(n）为该数列的第n项（n∈N*），那么这句话可以写成如下形式：

显然这是一个线性递推数列。

通项公式

下面看看Ackerman函数：

Fibonacci数列可以写出通项公式，就是用非递归的方式去下定义。但并非一切的递归函数都能用非递归方式去定义。下面讲一个双递归函数——Ackerman函数，它的复杂性就比Fibonacci数列递归公式要复杂多了。

百度百科：Ackerman函数  （其实下面百度百科关于Ackerman函数的描述大体是抄自王晓东的《算法设计与分析（第2版）》清华大学出版社第2章递归与分治策略例题2.3 。）

当一个函数及它的一个变量是由函数自身定义时，称这个函数是双递归函数.当两个连续函数都趋于无穷时，我们常用洛必达法则来比较它们趋向无穷的快慢。函数的阶越高，它趋向无穷的速度就越快。在定义在正整数域上的函数中，n!趋向于正无穷的速度非常快，所以在算法设计中如果出现这样的时间复杂度就太糟糕了。logn趋向无穷的速度则非常慢。

今天你将看到一个增长速度比n!快的多的函数和一个比logn慢的多的函数，它们都源于一个函数–’Ackerman Function’。

 Ackerman函数有A(n,m)有两个独立的整变量m>=0,n>=0，其定义如下

A(1,0)=2;

A(0,m)=1 m>=0

A(n,0)=n+2 n>=2

A(n,m)=A(A(n-1,m),m-1) n,m>=1

A(n,m)的每一个自变量都定义了一个单变量函数。递归式的第三式定义了函数“加2”。

m=1时,由于A(1,1)=A(A(0,1),0)=A(1,0)=2

以及A(n,1)=A(A(n-1),1),0)=A(n-1,1)+2  (n>1)，因此A(n,1)=2n (n>=1)，即A(n,1)定义了函数“乘2”

当m=2时，由于A(1,2)=A(A(0,2),1)=A(1,1)=2

A(n,2)=A(A(n-1,2),1)=2A(n-1,2)，因此A(n,2)=2^n

以此类推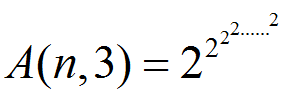，，其中2的层数为n。

A(n,4)的增长速度已经变得难以想象的快，以至于不能写出一个通项公式来表示这一函数。

下面再来考虑单变量Ackerman函数A(n):=A(n,n)。 设其逆函数为B(n):=min{k|A(k)>=n}，即B(n)是使n<=A(k)成立的最小k值。

由A(0)=1,A(1)=2,A(2)=4,A(3)=16推知B(1)=0,B(2)=1,B(3)=B(4)=2和B(5)=…=B(16)=3。由此可以看出B(n)的增长速度非常慢。

A(4)=222…2其中2的层数为65535，这个数有log(A(4))位。所以，对于通常所见到的正整数n，有B(n)<=4

但是理论上B(n)没有上界，随着n的增加，它将以难以想象的慢速度趋向正无穷大

Ackerman函数有A(n,m)有两个独立的整变量m>=0,n>=0，其定义如下

A(1,0)=2;

A(0,m)=1 m>=0

A(n,0)=n+2 n>=2

A(n,m)=A(A(n-1,m),m-1) n,m>=1

A(n,m)的自身变量m的每一个值都定义了一个单变量函数

维基百科：Ackerman函数的描述

定义如下：

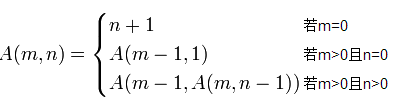
乍一看，这个定义和上面百度百科给的定义不太一样。仔细分析，其实它们两个A（）函数当中的m、n含义没变，只是参数当中顺序刚好相反而已。

下面是网友的代码：（来源：http://blog.csdn.net/gpengtao/article/details/7438587）

int ack(int m,int n)
{
    if(m == )
        return n+;
    else if(n == )
        return ack(m-,);
    else
        return ack(m-,ack(m,n-));
}