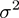Stanford机器学习笔记-8. 支持向量机(SVMs)概述
8. Support Vector Machines(SVMs)
Content
8. Support Vector Machines(SVMs)
8.1 Optimization Objection
8.2 Large margin intuition
8.3 Mathematics Behind Large Margin Classification
8.4 Kernels
8.5 Using a SVM
8.5.1 Multi-class Classification
8.5.2 Logistic Regression vs. SVMs
8.1 Optimization Objection
支持向量机(Support Vector Machine: SVM)是一种非常有用的监督式机器学习算法。首先回顾一下Logistic回归,根据log()函数以及Sigmoid函数的性质,有:
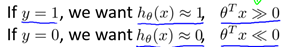
同时,Logistic回归的代价函数(未正则化)如下:
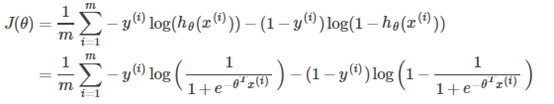
为得到SVM的代价函数,我们作如下修改:

因此,对比Logistic的优化目标

SVM的优化目标如下:
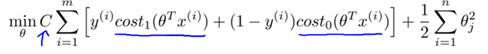
注1:事实上,上述公式中的Cost0与Cost1函数是一种称为hinge损失的替代损失(surrogate loss)函数,其他常见的替代损失函数有指数损失和对率损失,具体参见《机器学习》P129 周志华)
注2:注意参数C和λ的对应关系: C与(1 / λ)成正相关。
8.2 Large margin intuition
根据8.1中的代价函数,为使代价函数最小,有如下结论:
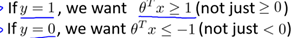
现假设C很大(如C=100000),为使代价函数最小,我们希望
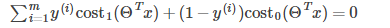
所以代价函数就变为:
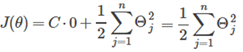
所以问题就变成:

该问题最后的优化结果是找到具有"最大间隔"(maximum margin)的划分超平面,所以支持向量机又称大间距分类器(large margin classifier)。那么什么是间隔? 为什么这样优化就可以找到最大间隔?首先,我们通过图8-1所示的二维的0/1线性分类情况来直观感受。
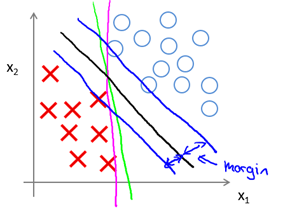
图8-1 SVM Decision Boundary: Linearly separable case
直观上,应该去找位于两类训练样本"正中间"的划分超平面,即图8-1的黑色直线(二维),因为该划分超平面对训练样本局部扰动的"容忍"性最好。例如,图中的粉色和绿色直线,一旦输入数据稍有变化,将会得到错误的预测。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对要预测数据集的泛化能力最强。而两条蓝色直线之间的距离就称为间隔(margin)。下一节将从数学角度来解释间隔与最大间隔的优化原理。
8.3 Mathematics Behind Large Margin Classification
首先介绍一些数学知识。
- 2-范数(2-norm): 也可称长度(length),是二维或三维空间向量长度的推广,向量u记为||u||。例如,对于向量u = [ u1, u2, u3, u4],||u|| = sqrt(u1^2 + u2^2 + u3^2 + u4^2)
- 向量内积(Vector Inner Product): 设向量a = [a1, a2, … , an],向量b = [b1, b2, … , bn],a和b的的内积定义为:a · b = a1b1 + a2b2 + … + anbn 。向量内积是几何向量数量积(点积)的推广,可以理解为向量a在向量b上的投影长度(范数)和向量b的长度的乘积。
所以有:

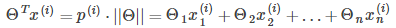
其中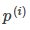 是
是 在
在 向量上的投影长度。
向量上的投影长度。
所以,8.2节得到的优化问题可以转为如下形式:
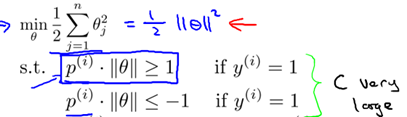
分界线为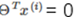 ,所以可知
,所以可知 和分界线正交(垂直),并且当
和分界线正交(垂直),并且当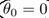 时,分界线过原点(欧式空间)。为使目标最优(取最小值)且满足约束,
时,分界线过原点(欧式空间)。为使目标最优(取最小值)且满足约束,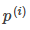 应该尽可能大,这样就要求间距尽可能的大。直观的如图8-2所示,图左为间距较小的情况,此时的
应该尽可能大,这样就要求间距尽可能的大。直观的如图8-2所示,图左为间距较小的情况,此时的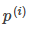 较小,为满足约束,导致目标函数变大,图右为最大间距的情况,此时的
较小,为满足约束,导致目标函数变大,图右为最大间距的情况,此时的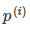 是最大的,所以目标可以尽可能的小。
是最大的,所以目标可以尽可能的小。

图8-2 两种不同间距的情况
8.4 Kernels
上述的讨论都是基于线性可分的样本,即存在一个划分超平面可以将训练样本正确分类,然而现实世界存在大量复杂的,非线性分类问题(如4.4.2节的异或/同或问题)。Logistic回归处理非线性问题可以通过引入多项式特征量作为新的特征量;神经网络通过引入隐藏层,逐层进化解决非线性分类问题;而SVM是通过引入核函数(kernel function)来解决非线性问题。具体做法如下:
- 对于给定输出x, 规定一定数量的landmarks,记为
 ;
; - 将x,
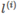 作为核函数的输入,得到新的特征量
作为核函数的输入,得到新的特征量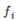 ,若将核函数记为similarity(),则有
,若将核函数记为similarity(),则有 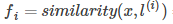 ,其中
,其中 与
与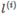 为一一对应;
为一一对应; - 将新的特征量替代原有特征量,得到假设函数如下:

现在有两个问题,
- 如何选择landmarks?
- 用什么样的核函数 ?
对于第一个问题,可以按照如下方式,即将训练集的输入作为landmarks

所以特征量的个数与训练集的个数相等,即n = m,所以带有核的SVM变为如下形式:

对于第二个问题,常用的核函数有线性核,高斯核,多项式核,Sigmoid核,拉普拉斯核等,现以常用的高斯核(Gaussian)为例。

高斯核具有如下性质:

也就是说,如果x和landmark接近,那么核函数的值也就是新的特征量将会接近1,而如果x和landmark距离很远,那么核函数的值将会接近0.
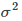 是高斯核的参数,它的大小会影响核函数值的变化快慢,具体的,图8-3是一个二维情况下的特殊例子,但是所含有的性质是可推广的。即
是高斯核的参数,它的大小会影响核函数值的变化快慢,具体的,图8-3是一个二维情况下的特殊例子,但是所含有的性质是可推广的。即 越大,核函数变化(下降)越缓慢,反之,
越大,核函数变化(下降)越缓慢,反之,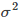 越小,核函数变化越快。
越小,核函数变化越快。

图8-3 参数对高斯核的影响举例
- 如何选择参数?
下面对SVM的参数对偏差和方差的影响做简要分析:
- C: 由于C和(1 / λ)正相关,结合6.4.2节对λ的分析有:
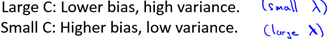

8.5 Using a SVM
上文简单的介绍了SVM的优化原理以及核函数的使用方式。在实际应用SVM中,我们不需要自己去实现SVM的训练算法来得到参数 ,通常是使用现有的软件包(如liblinear, libsvm)。
,通常是使用现有的软件包(如liblinear, libsvm)。
但是下面的工作是我们需要做的:
- 选择参数C的值
- 选择并实现核函数
- 如果核函数带参数,需要选择核函数的参数,例如高斯核需要选择
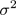
- 如果无核(选择线性核),即给出线性分类器,适用于n大,m小的情况
- 选择非线性核(如高斯核),适用于n小,m大的情况
下面是需要注意的地方:
- 在使用核函数之前要对特征量进行规范化
- 并不是所有的函数是有效的核函数,它们必须满足Mercer定理。
- 如果想要通过训练得到参数C或者核函数的参数,应该是在训练集和交叉检验集上进行,,参见6.3节。
8.5.1 Multi-class Classification

8.5.2 Logistic Regression vs. SVMs

参考:《机器学习》 周志华
Stanford机器学习笔记-8. 支持向量机(SVMs)概述的更多相关文章
- [吴恩达机器学习笔记]12支持向量机5SVM参数细节
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.5 SVM参数细节 标记点选取 标记点(landma ...
- [吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.3 大间距分类背后的数学原理- Mathematic ...
- [吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.2 大间距的直观理解- Large Margin I ...
- [吴恩达机器学习笔记]12支持向量机1从逻辑回归到SVM/SVM的损失函数
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.1 SVM损失函数 从逻辑回归到支持向量机 为了描述 ...
- Stanford机器学习笔记-9. 聚类(Clustering)
9. Clustering Content 9. Clustering 9.1 Supervised Learning and Unsupervised Learning 9.2 K-means al ...
- Stanford机器学习笔记-9. 聚类(K-means算法)
9. Clustering Content 9. Clustering 9.1 Supervised Learning and Unsupervised Learning 9.2 K-means al ...
- 机器学习笔记:支持向量机(svm)
支持向量机(svm)英文为Support Vector Machines 第一次接触支持向量机是2017年在一个在线解密游戏"哈密顿行动"中的一个关卡的二分类问题,用到了台湾教授写 ...
- Stanford机器学习笔记-10. 降维(Dimensionality Reduction)
10. Dimensionality Reduction Content 10. Dimensionality Reduction 10.1 Motivation 10.1.1 Motivation ...
- Stanford机器学习笔记-7. Machine Learning System Design
7 Machine Learning System Design Content 7 Machine Learning System Design 7.1 Prioritizing What to W ...
随机推荐
- Spirit - 腾讯移动 Web 整体解决方案
Spirit 并不是一个具体的框架或者工具,但是她是移动端一系列解决方案的整合与聚拢.她是腾讯 Alloyteam 开发团队在移动开发项目中通过大量实践.归纳.总结提炼而成,最终沉淀下来的一个体系,真 ...
- 最简单的轮播广告(原生JS)
改变每个图片的opacity属性:来自学友刘斌 素材图片: <!DOCTYPE html> <html lang="en"> <head> &l ...
- Session Storage、Cache Storage
Session Storage sessionStorage用于本地存储一个会话(session)的数据,这些数据只有在同一个会话中的页面才能访问并且当会话结束后数据也随之销毁(浏览器关闭).因此se ...
- 利用JSONP实现跨域请求
前言:有时候一忙起来就没了时间观念,原来我已经有十多天没写博客了.一直想做跨域方面的尝试,无奈最近准备校招没时间动动手.今天就先讲讲JSONP吧,昨晚还在研究QQ空间日志里面网络图片的问题呢,我发现日 ...
- CSS常用样式(三)
一.2D变换 1.transform 设置或检索对象的转换 取值: none::以一个含六值的(a,b,c,d,e,f)变换矩阵的形式指定一个2D变换,相当于直接应用一个[a,b,c,d,e,f] ...
- [转]很详细的devexpress应用案例
很详细的devexpress应用案例,留着以后参考. 注:转载自http://***/zh-CN/App/Feature.aspx?AppId=50021 UPMS(User Permissions ...
- 在Sharepoint 2013中,使用JS判断当前用户是否在某个组里面
使用Sharepoint客户端对象模型,判断当前用户是否在某个组里面. 在View 和 Edit List Item的时候使用,使用户编辑修改List Item的时候有权限的区分. 在Edit 页面加 ...
- SPS中使用JSOM发邮件
直接上代码了: function ShowMailDialog() { $.ajax({ url: siteurl + "/_api/contextinfo", method: & ...
- Android TextView走马灯效果
布局: <TextView android:id="@+id/myTextView" android:layout_width="match_parent" ...
- Android保持屏幕常亮的方法
以前一直使用newWakeLock方法: this.powerManager = (PowerManager) this .getSystemService(Context.POWER_SERVICE ...