【cs229-Lecture15】奇异值分解
PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值分解去实现的。
内容:
- PCA (主成份分析)是一种直接的降维方法,通过求解特征值与特征向量,并选取特征值较大的一些特征向量来达到降维的效果;
- PCA 的一个应用——LSI(Latent Semantic Indexing, 隐含语义索引);
- PCA 的一个实现——SVD(Singular Value Decomposition,奇异值分解);
- ICA(独立成份分析)
隐含语义索引(LSI)
什么叫LSI?
所谓隐性语义索引指的是,怎样通过海量文献找出词汇之间的关系。当两个词或一组词大量出现在同一个文档中时,这些词之间就可以被认为是语义相关。机器并不知道某个词究竟代表什么,不知道某个词是什么意思。
比如:
(1)电脑和计算机这两个词在人们写文章时经常混用,这两个词在大量的网页中同时出现,搜索引擎就会认为这两个词是极为语义相关的。 (2)SEO和搜索引擎优化(虽然一个是英语,一个是中文)这两个词大量出现在相同的网页中,虽然搜索引擎还不能知道搜索引擎优化或SEO指的是什么,但是却可以从语义上把”SEO”,”搜索引擎优化”,”Search Engine optimization”,”SEM”等词紧紧的连在一起。可见潜在语义索引并不依赖于语言。
(3)如苹果和橘子这两个词,也是大量出现在相同文档中,不过紧密度低于同义词。所以搜索引擎不会认为它们是语义相关的。
向量表示文本,维度高。那么啥是隐含语义索引呢?在主成分分析中隐含语义索引的意思就是通过降维的手段,将意义相同的词映射到低维空间中的同一个维度上去。这样一可以降低计算复杂度,二可以减少噪声。其中,减少噪声是指两个在高维上完全不相似的文本通过降维以后可能变得相似了。比如,假如有一篇文章,只包含一个单词 learn,另一篇文章只包含 study,在高维上计算相似度为 0,通过隐含语义索引,将 learn 和 study 映射到同一维上,再计算相似度就更精确了。
SVD(Singular Value Decomposition,奇异值分解)
转自:http://blog.csdn.net/ningyaliuhebei/article/details/7104951
奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。
在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing)
以下转自:http://blog.csdn.net/wangzhiqing3/article/details/7446444
基础知识
1. 矩阵的秩:矩阵的秩是矩阵中线性无关的行或列的个数
2. 对角矩阵:对角矩阵是除对角线外所有元素都为零的方阵
3. 单位矩阵:如果对角矩阵中所有对角线上的元素都为1,该矩阵称为单位矩阵
4. 特征值:对一个M x M矩阵C和向量X,如果存在λ使得下式成立

则称λ为矩阵C的特征值,X称为矩阵的特征向量。非零特征值的个数小于等于矩阵的秩。
5. 特征值和矩阵的关系:考虑以下矩阵

该矩阵特征值λ1 = 30,λ2 = 20,λ3 = 1。对应的特征向量

假设VT=(2,4,6) 计算S x VT


有上面计算结果可以看出,矩阵与向量相乘的结果与特征值,特征向量有关。观察三个特征值λ1 = 30,λ2 = 20,λ3 = 1,λ3值最小,对计算结果的影响也最小,如果忽略λ3,那么运算结果就相当于从(60,80,6)转变为(60,80,0),这两个向量十分相近。这也表示了数值小的特征值对矩阵-向量相乘的结果贡献小,影响小。这也是后面谈到的低阶近似的数学基础。
矩阵分解
1. 方阵的分解
1) 设S是M x M方阵,则存在以下矩阵分解

其中U 的列为S的特征向量, 为对角矩阵,其中对角线上的值为S的特征值,按从大到小排列:
为对角矩阵,其中对角线上的值为S的特征值,按从大到小排列:

2) 设S是M x M 方阵,并且是对称矩阵,有M个特征向量。则存在以下分解

其中Q的列为矩阵S的单位正交特征向量, 仍表示对角矩阵,其中对角线上的值为S的特征值,按从大到小排列。最后,QT=Q-1,因为正交矩阵的逆等于其转置。
仍表示对角矩阵,其中对角线上的值为S的特征值,按从大到小排列。最后,QT=Q-1,因为正交矩阵的逆等于其转置。
2. 奇异值分解
上面讨论了方阵的分解,但是在LSA中,我们是要对Term-Document矩阵进行分解,很显然这个矩阵不是方阵。这时需要奇异值分解对Term-Document进行分解。奇异值分解的推理使用到了上面所讲的方阵的分解。
假设C是M x N矩阵,U是M x M矩阵,其中U的列为CCT的正交特征向量,V为N x N矩阵,其中V的列为CTC的正交特征向量,再假设r为C矩阵的秩,则存在奇异值分解:

其中CCT和CTC的特征值相同,为
Σ为M X N,其中
 ,其余位置数值为0,
,其余位置数值为0, 的值按大小降序排列。以下是Σ的完整数学定义:
的值按大小降序排列。以下是Σ的完整数学定义:

σi称为矩阵C的奇异值。
用C乘以其转置矩阵CT得:

上式正是在上节中讨论过的对称矩阵的分解。
奇异值分解的图形表示:

从图中可以看到Σ虽然为M x N矩阵,但从第N+1行到M行全为零,因此可以表示成N x N矩阵,又由于右式为矩阵相乘,因此U可以表示为M x N矩阵,VT可以表示为N x N矩阵
3. 低阶近似
LSA潜在语义分析中,低阶近似是为了使用低维的矩阵来表示一个高维的矩阵,并使两者之差尽可能的小。本节主要讨论低阶近似和F-范数。
给定一个M x N矩阵C(其秩为r)和正整数k,我们希望找到一个M x N矩阵Ck,其秩不大于K。设X为C与Ck之间的差,X=C – Ck,X的F-范数为

当k远小于r时,称Ck为C的低阶近似,其中X也就是两矩阵之差的F范数要尽可能的小。
SVD可以被用与求低阶近似问题,步骤如下:
1. 给定一个矩阵C,对其奇异值分解:
2. 构造 ,它是将
,它是将 的第k+1行至M行设为零,也就是把
的第k+1行至M行设为零,也就是把 的最小的r-k个(the r-k smallest)奇异值设为零。
的最小的r-k个(the r-k smallest)奇异值设为零。
3. 计算Ck:
回忆在基础知识一节里曾经讲过,特征值数值的大小对矩阵-向量相乘影响的大小成正比,而奇异值和特征值也是正比关系,因此这里选取数值最小的r-k个特征值设为零合乎情理,即我们所希望的C-Ck尽可能的小。完整的证明可以在Introduction to Information Retrieval[2]中找到。
我们现在也清楚了LSA的基本思路:LSA希望通过降低传统向量空间的维度来去除空间中的“噪音”,而降维可以通过SVD实现,因此首先对Term-Document矩阵进行SVD分解,然后降维并构造语义空间。
在 SVD 的最后,Ng 总结出一张表。 
表格中的内容很好理解,Ng 特地强调的是这样的思考方式,寻找算法中的相同点和不
同点有利于更好的理解算法。
ICA(独立成份分析)





2. ICA的不确定性(ICA ambiguities)
由于w和s都不确定,那么在没有先验知识的情况下,无法同时确定这两个相关参数。比如上面的公式s=wx。当w扩大两倍时,s只需要同时扩大两倍即可,等式仍然满足,因此无法得到唯一的s。同时如果将人的编号打乱,变成另外一个顺序,如上图的蓝色节点的编号变为3,2,1,那么只需要调换A的列向量顺序即可,因此也无法单独确定s。这两种情况称为原信号不确定。
还有一种ICA不适用的情况,那就是信号不能是高斯分布的。假设只有两个人发出的声音信号符合多值正态分布,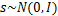 ,I是2*2的单位矩阵,s的概率密度函数就不用说了吧,以均值0为中心,投影面是椭圆的山峰状(参见多值高斯分布)。因为
,I是2*2的单位矩阵,s的概率密度函数就不用说了吧,以均值0为中心,投影面是椭圆的山峰状(参见多值高斯分布)。因为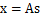 ,因此,x也是高斯分布的,均值为0,协方差为
,因此,x也是高斯分布的,均值为0,协方差为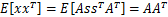 。
。
令R是正交阵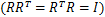 ,
,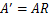 。如果将A替换成A’。那么
。如果将A替换成A’。那么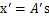 。s分布没变,因此x’仍然是均值为0,协方差
。s分布没变,因此x’仍然是均值为0,协方差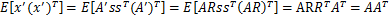 。
。
因此,不管混合矩阵是A还是A’,x的分布情况是一样的,那么就无法确定混合矩阵,也就无法确定原信号。
3. 密度函数和线性变换
在讨论ICA具体算法之前,我们先来回顾一下概率和线性代数里的知识。
假设我们的随机变量s有概率密度函数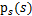 (连续值是概率密度函数,离散值是概率)。为了简单,我们再假设s是实数,还有一个随机变量x=As,A和x都是实数。令
(连续值是概率密度函数,离散值是概率)。为了简单,我们再假设s是实数,还有一个随机变量x=As,A和x都是实数。令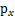 是x的概率密度,那么怎么求
是x的概率密度,那么怎么求 ?
?
令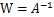 ,首先将式子变换成
,首先将式子变换成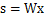 ,然后得到
,然后得到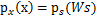 ,求解完毕。可惜这种方法是错误的。比如s符合均匀分布的话(
,求解完毕。可惜这种方法是错误的。比如s符合均匀分布的话(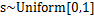 ),那么s的概率密度是
),那么s的概率密度是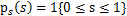 ,现在令A=2,即x=2s,也就是说x在[0,2]上均匀分布,可知
,现在令A=2,即x=2s,也就是说x在[0,2]上均匀分布,可知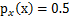 。然而,前面的推导会得到
。然而,前面的推导会得到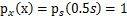 。正确的公式应该是
。正确的公式应该是
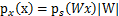
推导方法
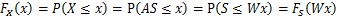
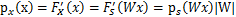
更一般地,如果s是向量,A可逆的方阵,那么上式子仍然成立。
4. ICA算法
ICA算法归功于Bell和Sejnowski,这里使用最大似然估计来解释算法,原始的论文中使用的是一个复杂的方法Infomax principal。
我们假定每个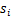 有概率密度
有概率密度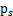 ,那么给定时刻原信号的联合分布就是
,那么给定时刻原信号的联合分布就是

这个公式代表一个假设前提:每个人发出的声音信号各自独立。有了p(s),我们可以求得p(x)
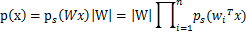
左边是每个采样信号x(n维向量)的概率,右边是每个原信号概率的乘积的|W|倍。
前面提到过,如果没有先验知识,我们无法求得W和s。因此我们需要知道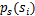 ,我们打算选取一个概率密度函数赋给s,但是我们不能选取高斯分布的密度函数。在概率论里我们知道密度函数p(x)由累计分布函数(cdf)F(x)求导得到。F(x)要满足两个性质是:单调递增和在[0,1]。我们发现sigmoid函数很适合,定义域负无穷到正无穷,值域0到1,缓慢递增。我们假定s的累积分布函数符合sigmoid函数
,我们打算选取一个概率密度函数赋给s,但是我们不能选取高斯分布的密度函数。在概率论里我们知道密度函数p(x)由累计分布函数(cdf)F(x)求导得到。F(x)要满足两个性质是:单调递增和在[0,1]。我们发现sigmoid函数很适合,定义域负无穷到正无穷,值域0到1,缓慢递增。我们假定s的累积分布函数符合sigmoid函数
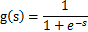
求导后
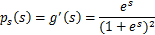
这就是s的密度函数。这里s是实数。
如果我们预先知道s的分布函数,那就不用假设了,但是在缺失的情况下,sigmoid函数能够在大多数问题上取得不错的效果。由于上式中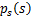 是个对称函数,因此E[s]=0(s的均值为0),那么E[x]=E[As]=0,x的均值也是0。
是个对称函数,因此E[s]=0(s的均值为0),那么E[x]=E[As]=0,x的均值也是0。
知道了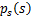 ,就剩下W了。给定采样后的训练样本
,就剩下W了。给定采样后的训练样本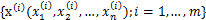 ,样本对数似然估计如下:
,样本对数似然估计如下:
使用前面得到的x的概率密度函数,得
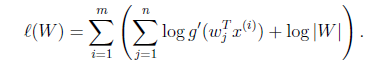
大括号里面是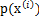 。
。
接下来就是对W求导了,这里牵涉一个问题是对行列式|W|进行求导的方法,属于矩阵微积分。这里先给出结果,在文章最后再给出推导公式。
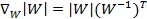
最终得到的求导后公式如下,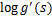 的导数为
的导数为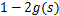 (可以自己验证):
(可以自己验证):
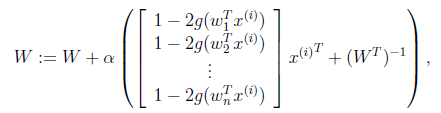
其中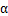 是梯度上升速率,人为指定。
是梯度上升速率,人为指定。
当迭代求出W后,便可得到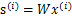 来还原出原始信号。
来还原出原始信号。
注意:我们计算最大似然估计时,假设了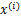 与
与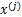 之间是独立的,然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上,这个假设不能成立。但是在数据足够多时,假设独立对效果影响不大,同时如果事先打乱样例,并运行随机梯度上升算法,那么能够加快收敛速度。
之间是独立的,然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上,这个假设不能成立。但是在数据足够多时,假设独立对效果影响不大,同时如果事先打乱样例,并运行随机梯度上升算法,那么能够加快收敛速度。
回顾一下鸡尾酒宴会问题,s是人发出的信号,是连续值,不同时间点的s不同,每个人发出的信号之间独立(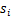 和
和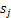 之间独立)。s的累计概率分布函数是sigmoid函数,但是所有人发出声音信号都符合这个分布。A(W的逆阵)代表了s相对于x的位置变化,x是s和A变化后的结果。
之间独立)。s的累计概率分布函数是sigmoid函数,但是所有人发出声音信号都符合这个分布。A(W的逆阵)代表了s相对于x的位置变化,x是s和A变化后的结果。
实例:



6. 行列式的梯度
对行列式求导,设矩阵A是n×n的,我们知道行列式与代数余子式有关,
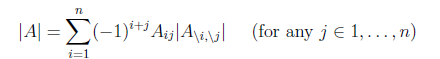
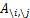 是去掉第i行第j列后的余子式,那么对
是去掉第i行第j列后的余子式,那么对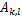 求导得
求导得
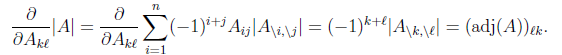
adj(A)跟我们线性代数中学的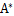 是一个意思,因此
是一个意思,因此
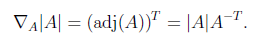
【cs229-Lecture15】奇异值分解的更多相关文章
- 资源 | 源自斯坦福CS229,机器学习备忘录在集结
在 Github 上,afshinea 贡献了一个备忘录对经典的斯坦福 CS229 课程进行了总结,内容包括监督学习.无监督学习,以及进修所用的概率与统计.线性代数与微积分等知识. 项目地址:http ...
- 奇异值分解(SVD)原理与在降维中的应用
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...
- SVD奇异值分解的基本原理和运用
SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...
- 奇异值分解(SVD)和简单图像压缩
SVD(Singular Value Decomposition,奇异值分解) 算法优缺点: 优点:简化数据,去除噪声,提高算法结果 缺点:数据的转换可能难于理解 适用数据类型:数值型数据 算法思想: ...
- 数值分析之奇异值分解(SVD)篇
在很多线性代数问题中,如果我们首先思考若做SVD,情况将会怎样,那么问题可能会得到更好的理解[1]. --Lloyd N. ...
- 强大的矩阵奇异值分解(SVD)及其应用
版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...
- 利用奇异值分解(SVD)简化数据
特征值与特征向量 下面这部分内容摘自:强大的矩阵奇异值分解(SVD)及其应用 特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法.两者有着很紧密的关系,在接下来会谈到,特征值分解和奇异值分解的 ...
- SVD奇异值分解
奇异值分解 备忘:Eigen类库可能会和其他库产生冲突,将Eigen类库的头文件引用放到前面解决了.
- 矩阵奇异值分解(SVD)及其应用
机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用(好文) [简化数据]奇异值分解(SVD) <数学之美> 第15章 矩阵运算和文本处理中的两个分类问题
随机推荐
- vs emulator for android使用
在windows上调试android程序,可以利用hyperv虚拟化功能,微软也提供了模拟工具和android studio.eclipse的配置说明,不再累述. 关于启动vs模拟器的cmd命令: e ...
- 浅析JVM中的GC日志
目录 一.GC日志的格式分析 二.运行时开启GC日志 一.GC日志的格式分析 在讲述GC日志之前,我们先来运行下面这段代码 package com.example; public class Test ...
- Null Object模式
去除代码中的if(obj==null),或者try/catch语句.维持Code的一致性. Null对象,代表"什么也不做"的一个对象. 使Null对象称为一个匿名内部类确保了该类 ...
- bzoj 3399: [Usaco2009 Mar]Sand Castle城堡
3399: [Usaco2009 Mar]Sand Castle城堡 Time Limit: 3 Sec Memory Limit: 128 MB Description 约翰用沙子建了一座城堡.正 ...
- 详解Bootstrap网格系统
bootstrap框架中的网格系统就是将容器平分成12份,在使用的时候可以根据实际情况重新编译LESS/SASS源码来修改12这个数值.bootstrap框架的网格系统工作原理: 1.数据行(.row ...
- Android 发布可穿戴设备 SDK 的开发者预览版
今早上安卓官网查资料,发现网站上赫然显示着"Android Wear"几个大字.难道……?点进去看,果然,Android发布了可穿戴设备的SDK的开发者预览版. 其中这第五张图…… ...
- linux 下查找大于100M的文件(转)
命令行如下 find . -type f -size +1000000k Linux系统下查找大文件或目录的技巧 当硬盘空间不够时,我们就很关心哪些目录或文件比较大,看看能否干掉一些了,怎么才能知道呢 ...
- GO語言基礎教程:流程控制
在開始一個新的章節之前先來回顧上一篇文章的部份,首先我們來看這段代碼: package main import ( "fmt" ) func main(){ var x,y int ...
- 【CUDA学习】全局存储器
全局存储器,即普通的显存,整个网格中的任意线程都能读写全局存储器的任意位置. 存取延时为400-600 clock cycles 非常容易成为性能瓶颈. 访问显存时,读取和存储必须对齐,宽度为4By ...
- swift入门篇-函数
今天给大家介绍 swift函数,swift函数和c#,js的写法大致一直,但是与object-c写法有很大不同点.废话不多说,直接开始了. 1:函数 --常量参数 func 函数名( 参数变量:类型 ...
