二叉索引树BIT

定义

    二叉索引树，binary index tree，又名树状数组，或Fenwick Tree，因为本算法由Fenwick创造。

    对于数组A，定义Query(i,j) = Ai +Ai+1 + … + Aj.

    比较好的做法：使用前缀和，Sum(j) – Sum(i-1)即可得到Query(i,j)

    BIT即为解决此类区间查询而大展身手，因为预处理时间为O(n)，之后的查询时间为O(1)，是属于典型的在线算法(关于在线算法，通俗地可以理解为，做一次预处理，提供多次“服务”——比如多次Query(i,j))。

Lowbit(nature)

    首先，定位lowbit(natural)为自然数(即1,2,3…n)的二进制形式中最右边出现1的值。

    比如：4 = 100，lowbit(4) = 4；36 = 100100，lowbit(36) = 4.

    自然数在二进制形式下，有如下的性质：

    Lowbit为1的自然数为1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31…d = 2

    Lowbit为2的自然数为2,6,10,14,18,22,26,30,… d = 4

    Lowbit为3的自然数为4,12,20,28… d=8

    Lowbit为4的自然数为8,32

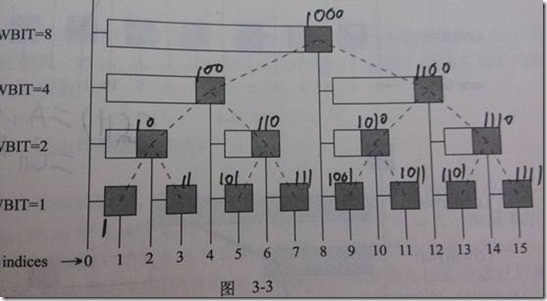
    直接上刘汝佳的算法竞赛入门竞赛经典中的图片：

    

    树状性质：对于节点i,如果他是左子结点，那么父节点的编号就是i+lowbit(i)；如果它是右子节点，那么父节点的编号是i-lowbit(i)。

    令数组C为：

     Ci = A_{i-lowbit(i)+1}+A _{i-lowbit(i)+2}+…A_i

    即从最左边的孩子，到自身的和，如C12 = A9(上图中最左边的儿子)+A10+A11+A12，C6=A5+A6。

    计算前缀和Sum(i)的计算：

    顺着节点i往左走，边走边“往上爬”，把经过的Ci 累加起来即可。

API

    l lowbit(idx)

      求A[idx]的低位

    l Sum(i)

     求区间1，i的前缀和

    l Add(idx,value)

      使节点idx的值增加value；

代码：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace Algorithms.Data_Structure
{
    /// <summary>
    /// 二叉索引树（树状数组：Fenwick Tree）
    /// </summary>
    public class BinaryIndexedTree
    {
        /// <summary>
        /// 处理的数组
        /// </summary>
        private List<int> array;

        /// <summary>
        /// 二叉前缀和
        /// </summary>
        private List<int> tree;

        /// <summary>
        /// 个数
        /// </summary>
        private int n;

        public BinaryIndexedTree(int[] array)
        {
            this.array = new List<int>(array);
            this.n = this.array.Count;

            PreProcessing();
        }

        /// <summary>
        /// 预处理函数：每次增加数值
        /// </summary>
        private void PreProcessing()
        {
            tree = new List<int>(n);
            for (int ii = 0; ii < n; ii++)
            {
                tree.Add(0);
            }

            for (int ii = 1; ii < n; ii++)
            {
                Update(ii, array[ii]);
            }
        }

        /// <summary>
        /// 二进制形式中的最右边的1所对应的值，如38288 = 1001010110010000 ，则返回16
        /// </summary>
        /// <param name="idx"></param>
        private int lowbit(int idx)
        {
            return idx & (-idx);
        }

        /// <summary>
        /// 在x处加v
        /// </summary>
        /// <param name="idx">数组的索引，从1开始计数</param>
        /// <param name="v">值</param>
        public void Update(int idx, int v)
        {
            while (idx < n)
            {
                tree[idx] += v;
                idx += lowbit(idx); //left's parent
            }
        }

        /// <summary>
        /// 从0到x求和
        /// </summary>
        /// <param name="idx">索引，从1开始计数</param>
        /// <returns>求和结果</returns>
        public int Sum(int idx)
        {
            int ret = 0;
            while (idx > 0)
            {
                ret += tree[idx];
                idx -= lowbit(idx); // right's parent
            }
            return ret;
        }
    }
}

Test:

class Program
{
    static void Main(string[] args)
    {
        BinaryIndexedTree bit = new BinaryIndexedTree(new int[] { 0, 1, 2, 3, 4, 5 }); //从1开始计数
        Console.WriteLine(bit.Sum(5));//15
        bit.Update(4, 23);
        Console.WriteLine(bit.Sum(5));//38
    }
}