Involution：空间不共享？可完全替代卷积的高性能算子 | CVPR 2021

其实这篇文章很早就写好了，但作者其它论文涉及到洗稿问题，所以先放着了。目前看这篇文章没被举报有洗稿的嫌疑，所以就发出来了

.

来源：晓飞的算法工程笔记 公众号

论文: Involution: Inverting the Inherence of Convolution for Visual Recognition

• 论文地址：https://arxiv.org/abs/2103.06255
• 论文代码：https://github.com/d-li14/involution

Introduction

---

  论文认为卷积操作有三个问题：

• 空间不变(spatial-agnostic)的计算方式虽然节省参数以及带来平移不变性，却也剥夺了卷积从不同位置发掘不同特征的能力。
• 常用的卷积核大小为\(3\times 3\)，过小的感受野会约束与长距离特征的互动，限制特征提取能力。
• 卷积核的冗余性已经被广泛地发现。

  为了解决上述的问题，论文提出了与卷积有相反属性的操作involution，核参数在空间上面特异，而在通道上面共享，主要有以下两个优点：

• 通道共享减少了大量参数，使得involution可以使用更大的核，从而能够捕捉长距离特征。
• 由于involution是空间特异的，相同的网络不同的输入会产生不同大小的特征图，对应的核大小也不一样，所以involution根据输入特征动态生成核参数，能够自适应地提取更多的视觉信息，达到类似attention的效果。

Design of Involution

---

  一组involution核可表示为\(\mathcal{H}\in \mathbb{R}^{H\times W\times K\times K\times G}\)，这里的分组与卷积相反，增加分组是为了增加核的复杂性。对于像素\(X_{i,j}\in \mathbb{R}^C\)，其involution核为\(\mathcal{H}_{i,j,\cdot,\cdot,g}\in \mathbb{R}^{K\times K}\)，\(g=1,2,\cdots,G\)为involtion核的分组，组内核共享。involution的特征图输出通过对输入特征进行Multiply-Add操作得到：

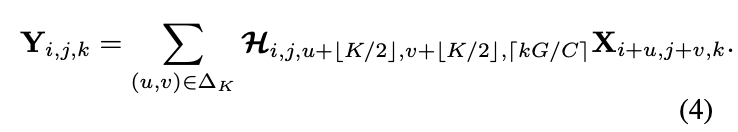
  \(k\)为通道编号，involution核的大小取决于输入特征图的大小，通过核生成函数\(\phi\)动态生成：

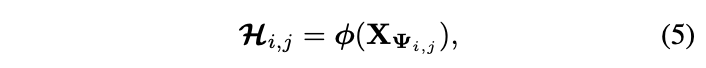
  \(\Psi_{i,j}\)为\(\mathcal{H}_{i,j}\)对应的输入像素合集。

Implementation Details

  为了简洁，论文直接从单个像素\(X_{i,j}\)生成对应的involution核\(\mathcal{H}_{i,j}\)，更复杂的结构也许能带来更好的性能，但不是当前主要的工作。定义核生成函数\(\phi\):\(\mathbb{R}^C\mapsto\mathbb{R}^{K\times K\times G}\)，\(\Psi_{i,j}=\{(i,j)\}\)：

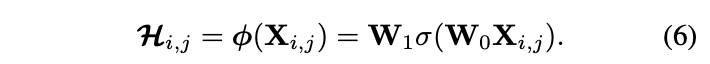
  \(W_0\in\mathbb{R}^{\frac{C}{r}\times C}\)和\(W_1\in\mathbb{R}^{(K\times K\times G)\times\frac{C}{r}}\)为线性变换，共同构成一个bottleneck结构，\(r\)为压缩因子，\(\sigma\)为BN+非线性激活。

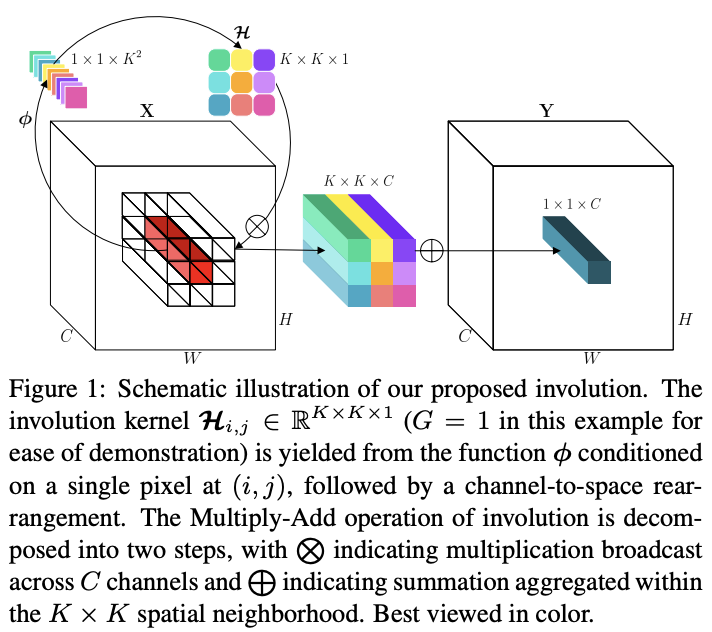
  公式4和公式6可表示为算法1和图1，在每个位置\((i,j)\)通过核生成函数生成对应的involution核，再对该位置进行计算得到输出。

  在构建完整的网络时，以ResNet作为基础，将stem(开头)的bottleneck中的\(3\times 3\)卷积替换成\(3\times 3\)或\(7\times 7\)的involution，将trunk(后续)的bottleneck中的\(3\times 3\)卷积替换成\(7\times 7\)的involution，\(1\times 1\)卷积保留用作通道融合与扩展。

  Involution的优势在于通道信息在核生成时利用了起来，并且后续使用较大的感受野获得更大的空间信息。另外在使用时，前后的\(1\times 1\)卷积也增加了通道交互，从而提升了整体的性能。

In Context of Prior Literature

---

  下面分别对involution进行两方面的探讨，分别是参数量下降的来源以及性能提升的来源。

Convolution and Variants

  Involution的思想十分简洁，从卷积的通道特异、空间共享转换成通道共享、空间特异，我们从参数量和计算量两块来进行分析(不考虑bias和involution的G)：

• 参数量方面，卷积和involution分别为\(C\times K\times K\times C\)和\(H\times W\times K\times K\times C\)，由于网络后续的特征图较小特点，involution能够节省大量的参数。
• 计算量方面，不考虑核生成部分，卷积和involtion分别为\(H\times W \times C\times K\times K\times C\)和\(H\times W\times K\times K\times C\)，由于involution在输出单像素结果时不需要像卷积那样综合多通道输入，计算量减少了一个量级。

  因为标准卷积实际上会融合多个输入通道进行输出，而且通道不共享，导致参数量和计算量都很高。而分组卷积减少了标准卷积中输出通道与输入通道之间的大量关联，和invlotion在参数量和计算量上有十分相似的地方：

• 参数量方面，分组卷积和involution分别为\(\frac{C}{G}\times K\times K\times C\)和\(H\times W\times K\times K\times G\)，而\(G=C\)的分组卷积和\(G=1\)的involution的参数量分别为\(K\times K\times C\)和\(H\times W\times K\times K\)，两者十分接近。
• 计算量方面，不考虑核生成部分，分组卷积和involution分别为\(\frac{C}{G}\times H\times W \times K\times K\times C\)和\(H\times W\times K\times K\times C\)，而\(G=C\)的分组卷积和\(G=1\)的involtion分别为\(H\times W\times K\times K\times C\)和\(H\times W\times K\times K\times C\)，两者完全一致。

  \(G=C\)的分组卷积即depthwise卷积，\(G=1\)的involution和depthwise卷积两者在结构上也可以认为是完全对立的，一个则通道共享、空间独立，另一个通道独立、空间共享，而在depthwise卷积上加上空间特异的属性即\(G=C\)的involution。但在之前很多的研究中，depthwise卷积一般都只用于轻量化网络的搭建，会牺牲部分准确率，而involution却能在减少部分参数量的同时提升准确率。我觉得除了空间特异带来大量参数之外，主要得益于两个部分设计：1）核大小增加到\(7\times 7\)。 2) 根据输入特征动态生成核参数。如果将depthwise卷积按类似的设置替换卷积核，不知道能否达到类似的结果。

Attention Mechanism

  self-attention起源于nlp任务，目前在视觉上的应用十分火热，有不错的性能表现。将输入向量线性转化成查询项\(Q\)、关键词项\(K\)以及值项\(V\)后，先用\(QK^{T}\)计算出相似性，再对值项加权后输出，大致的公式为：

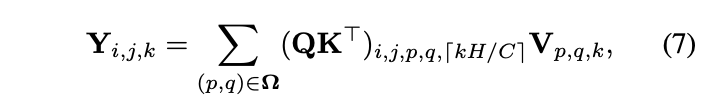
  如果将involution的核生成函数\(\mathcal{H}\)看成是\(QK^{T}\)的话，则可认为involution在某种意义上等同于self-attention，position encoding的信息也可认为是隐藏在了核生成函数里面，与生成的位置相关。文章花了很多篇幅去说明involution是self-attention的高层定义，有兴趣的可以去看看。不过我们只要理解，involution在特征图的不同位置动态生成了不同的核参数，功能上类似于self-attention中的attention即可，这也是involution能够提升准确率的关键。

Experiment

---

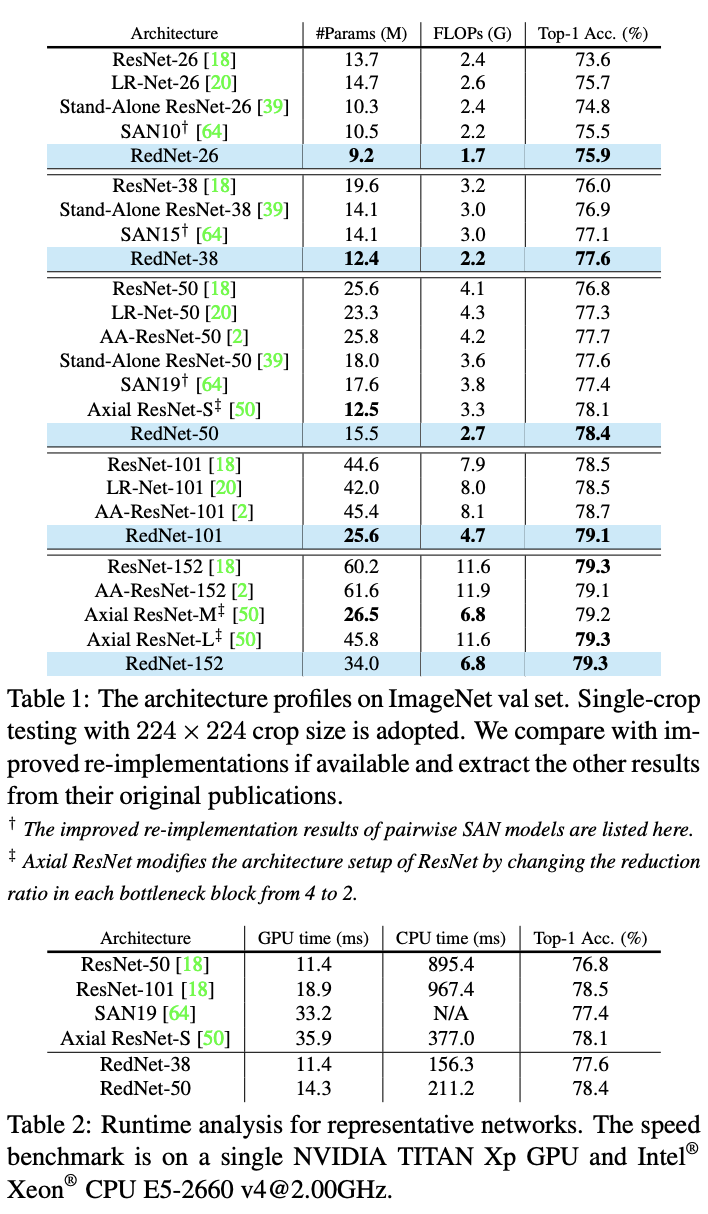
  从实验结果来看，由involution搭建的ReaNet能够在准确率提升的情况下减少大量的参数，从实际速度来看，GPU速度与ResNet差不多，CPU速度则提升很大。

Conclusion

---

  论文创新地提出了与卷积特性完全相反的基础算子Involution，该算子在通道上共享，而在空间上特异，不仅能够大幅减少参数量，还集成了attention的特性，在速度和准确率上都有很不错的表现。

 

 

 

如果本文对你有帮助，麻烦点个赞或在看呗～

更多内容请关注 微信公众号【晓飞的算法工程笔记】