[ARC144E]GCD of Path Weights

Problem Statement

You are given a directed graph $G$ with $N$ vertices and $M$ edges. The vertices are numbered $1, 2, \ldots, N$. The $i$-th edge is directed from Vertex $a_i$ to Vertex $b_i$, where $a_i < b_i$.

The beautifulness of a sequence of positive integers $W = (W_1, W_2, \ldots, W_N)$ is defined as the maximum positive integer $x$ that satisfies the following:

For every path $(v_1, \ldots, v_k)$ ($v_1 = 1, v_k = N$) from Vertex $1$ to Vertex $N$ in $G$, $\sum_{i=1}^k W_{v_i}$ is a multiple of $x$.

You are given an integer sequence $A = (A_1, A_2, \ldots, A_N)$. Find the maximum beautifulness of a sequence of positive integers $W = (W_1, \ldots, W_N)$ such that $A_i \neq -1 \implies W_i = A_i$. If the maximum beautifulness does not exist, print -1.

Constraints

$2\leq N\leq 3\times 10^5$
$1\leq M\leq 3\times 10^5$
$1\leq a_i < b_i \leq N$
$(a_i,b_i)\neq (a_j,b_j)$ if $i\neq j$
In the given graph $G$, there is a path from Vertex $1$ to Vertex $N$.
$A_i = -1$ or $1\leq A_i\leq 10^{12}$

Input

Input is given from Standard Input in the following format:

$N$ $M$

$a_1$ $b_1$

$\vdots$

$a_M$ $b_M$

$A_1$ $A_2$ $\ldots$ $A_N$

Output

Print the maximum beautifulness of a sequence of positive integers $W$. If the maximum beautifulness does not exist, print -1.

Sample Input 1

Sample Output 1

There are two paths from Vertex $1$ to Vertex $N$: $(1,2,4)$ and $(1,3,4)$.
For instance, $W = (5, 3, 7, 8)$ has a beautifulness of $4$. Indeed, both $W_1 + W_2 + W_4 = 16$ and $W_1 + W_3 + W_4 = 20$ are multiples of $4$.

Sample Input 2

Sample Output 2

There are three paths from Vertex $1$ to Vertex $N$: $(1,2,4)$, $(1,3,4)$, and $(1,4)$.
For instance, $W = (5, 3, 7, 8)$ has a beautifulness of $1$.

Sample Input 3

Sample Output 3

-1

For instance, $W = (3, 10^{100}, 10^{100}, 7)$ has a beautifulness of $10^{100}+10$. Since you can increase the beautifulness of $W$ as much as you want, there is no maximum beautifulness.

Sample Input 4

5 5

1 3

3 5

2 3

3 4

1 4

2 -1 3 -1 4

任意一条从 1 到 $n$ 的路径都是 $x$ 的倍数，这是一个很固定的要求。比如现在有这样的两条路径：

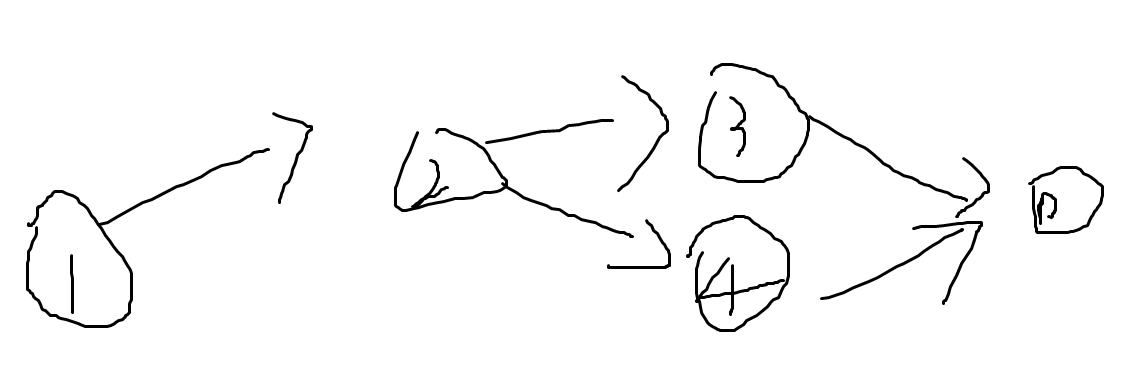
那么 $w_2+w_3+w_n=w_2+w_4+w_n(\bmod x)$

$w_2+w_3+w_n-w_2-w_4-w_n=0(\bmod x)$

这启发我们建一条反边，权值取反。

但权值在点上啊

拆点，把一个点拆成两个，中间的边的正的方向边权是点的权值，反的方向是点的权值取负。原来的单向边改为双向边，权值为0。此时我们想要让图只有 0 环。

只有0环的图有什么特点？从任意一个点出发，到某一个点的任意路径长度相等（又绕回了开头）。

那么如果此时从 $1$ 开始搜索,到达某一个点有一条路径距离 $d$，另一条是 $w$，那么 $x$ 整除 $|d-w|$

这样子不断求gcd，可以得到 $x$ 的限制。

但是如果点权为 $-1$?拆出来的两个点不连边。因为中间这条边可以随意决定。

注意要特判如果 $1$ 到 $n$ 是一个连通块，那么 $x$ 要和 $d_n$ 求一个 gcd.

小细节：所有 1 到不了的点和到不了 $n$ 的点都是不影响 $x$ 的，要去掉。

真的算一个神题了，知识点最难的也就dfs，但 rated 直飙 3280