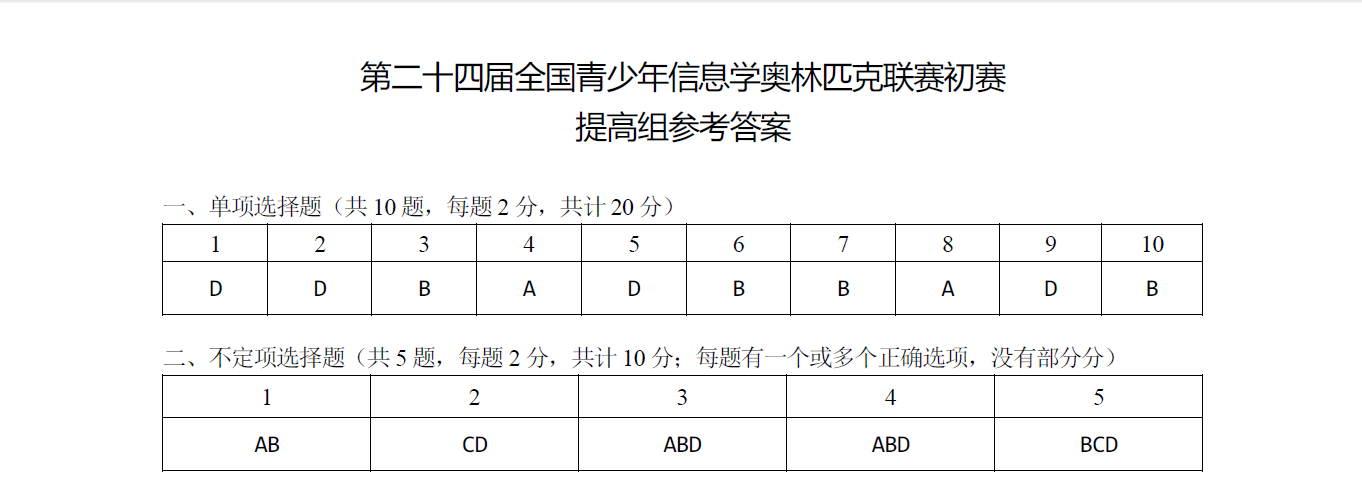
NOIp2018 提高组初赛试题参考答案


NOIp2018 提高组初赛试题参考答案的更多相关文章
- noip2018提高组初赛试题
一.单项选择题(共 10 题,每题 2 分,共计 20 分: 每题有且仅有一个正确选项) \2. 下列属于解释执行的程序设计语言是( ). A. C B. C++ C. Pascal D. Pytho ...
- NOIP 2018 提高组初赛试题 题目+答案+简要解析
一.单项选择题(共 10 题,每题 2 分,共计 20 分: 每题有且仅有一个正确选项) 1. 下列四个不同进制的数中,与其它三项数值上不相等的是( ). A. (269) 16 B ...
- NOIP2018提高组初赛知识点
(传说,在神秘的初赛中,选手们经常互相爆零以示友好……) 历年真题:ti.luogu.com.cn 以下标题中打*的是我认为的重点内容 一.关于计算机 (一)计算机组成 硬件组成: 1. 控制器(C ...
- NOIP2018提高组初赛准备
NOIP2017提高组初赛错题 一.单项选择题(共15 题,每题1.5 分,共计22.5 分:每题有且仅有一个正确选项) 4. 2017年10月1日是星期日,1949年10月1日是( ). A. 星期 ...
- NOIP2017普及组初赛试题及答案
普及组C++语言试题 一.单项选择题(共 20 题,每题 1.5 分,共计 30 分:每题有且仅有一个正确选项) 1.在 8 位二进制补码中,10101011 表示的数是十进制下的( ). A. 43 ...
- NOIP2018提高组初赛选讲
说实话,这次的初赛比上一次的要简单. 不过还有些变态的题目. 在一条长度为1 的线段上随机取两个点,则以这两个点为端点的线段的期望 长度是( ). A. 1 / 2 B. 1 / 3 C. 2 / 3 ...
- 【NOIP2012】提高组初赛试题(个人错题解析+相关知识点扩展)C++版
初赛14号就要开始了,从今天到14号还有三天,已经请了两节的自习来刷题,每天三四套题,尽量把01年到16年的题目全刷一遍.[fighting!!!] 4.无论是TCP/IP模型还是OSI模型,都可以视 ...
- NOIP2018提高组初赛游记
AH省的,好像水军多,走的都比较早(莫非是真·大佬!!) 本人考了71,较去年退步了.(去年还考80多的来着) 题目坑.. 第一.二大题选择 第三题年份,看了试卷标题,第二十二届,算出来后没有这个选项 ...
- 几道noip2018提高组初赛的题
以下做法来均自llj @Nicodafagood 一.单项选择题 7. 在一条长度为 1 的线段上随机取两个点,则以这两个点为端点的线段的期望 长度是( ).A. 1 / 2B. 1 / 3C. 2 ...
随机推荐
- css margin边界叠加问题详谈
问题:给子元素一个margin-top值,其父元素会跟着往下走margin-top的值 一.代码展示 HTML <body> <div class="box"&g ...
- android 在一个应用中启动另一个应用
在程序开发过程当中,常遇到需要启动另一个应用程序的情况,比如在点击软件的一个按钮可以打开地图软件. 如果既有包名又有主类的名字,那就好 办了, 直接像下面就行: [html] Intent inte ...
- GitHub笔记---邮箱访问错误
GitHub地址太长,所以需要一个变量来保存 把远程仓库赋值给一个变量,以后就用就这变量代表这个地址 GitHub推送push 推送过程中发生一个小插曲,出现了错误,错误提示我复制过来吧 remote ...
- LuoguP3964 [TJOI2013]松鼠聚会【切比雪夫距离/前缀和】
题目传送门 前置知识:切比雪夫距离和曼哈顿距离的相互转化--自为风月马前卒 有了这个知识,我们便可以在读入松鼠的家的坐标时,先把他转化一下,然后把最后的总式化简,我们会得到一个充满后缀和以及前缀和的式 ...
- 2019 年 Vue 学习路线图!
如果你是 Vue 开发新手,可能已经听过很多行话术语,比如单页面应用程序.异步组件.服务器端渲染,等等.你可能还听说过与 Vue 有关的一些工具和库,比如 Vuex.Webpack.Vue CLI 和 ...
- Nginx系列篇一:linux中安装Nginx
提示: 如遇到yum或者wget的问题, 请详见--->杂集:更换centos yum源 请详见--->杂集:关于VMware中linux使用NAT模式配置 1.安装nginx需要的环境 ...
- PHPmail 亲测可用
2017年5月8日9:10:47 1.在模块的配置文件中加入下里面代码,账号最好用126邮箱'THINK_EMAIL' => array( 'SMTP_HOST' => 'smtp.163 ...
- hdu1162 Eddy's picture 基础最小生成树
#include <cstdio> #include <cmath> #include <cstring> #include <algorithm> # ...
- iOS 优雅地隐藏导航栏NavigationBar (Objc)
@interface FSViewController () <UINavigationControllerDelegate> @end @implementation FSViewCon ...
- Python标准库 re
正则表达式 regular expression 用来匹配一系列符合句法规则的字符串,是一门独立的小型的语言,如果你了解类Unix系统,那么你对正则表达式就一定不陌生.正则表达式的概念最初是由Unix ...
