hdu 4923 Room and Moor [ 找规律 + 单调栈 ]

传送门

Room and Moor

Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1288    Accepted Submission(s): 416

Problem Description

PM Room defines a sequence A = {A₁, A₂,..., A_N}, each of which is either 0 or 1. In order to beat him, programmer Moor has to construct another sequence B = {B₁, B₂,... , B_N} of the same length, which satisfies that:

 

Input

The input consists of multiple test cases. The number of test cases T(T<=100) occurs in the first line of input.

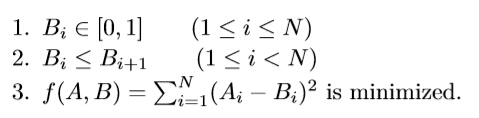
For each test case:
The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.
The second line consists of N integers, where the ith denotes A_i.

 

Output

Output the minimal f (A, B) when B is optimal and round it to 6 decimals.

 

Sample Input

4
9
1 1 1 1 1 0 0 1 1
9
1 1 0 0 1 1 1 1 1
4
0 0 1 1
4
0 1 1 1

 

Sample Output

1.428571
1.000000
0.000000
0.000000

 

Author

BUPT

 

Source

2014 Multi-University Training Contest 6

 

Recommend

We have carefully selected several similar problems for you:  5189 5184 5181 5180 5177 

又一道G++ T，C++ AC 的好题！！！！

题意及题解转自：

http://blog.csdn.net/a601025382s/article/details/38423069

题意：

给定一个长度为n的，由0和1组成的序列ai，求一个序列bi，使得∑(bi-ai)^2最小。其中0<=bi<=1,bi<=b(i+1)，bi为浮点型。输出最小的∑(bi-ai)^2的值。

题解：

对于ai序列中，开头的连续0,和结尾的连续1可以省略，因为bi中必定可以赋值连续0和连续1相同的值，使得(bi-ai)^2=0；

对于剩余的序列，我们可以分组，每组为连续1+连续0的形式（例如110010可以分成1100和10）。

对于每个组中的数ai，他们对应的bi必定是相同的。证：假设0对应的bi确定，那么要使∑(bi-ai)^2最小，1对应的bi肯定等于0对应bi中的最小值；同理1对应的bi确定时也一样。之后我们可以发现，这个值正好是rate=num1/(num1+num0)，numi表示i的个数。

之后我们遍历每个分组，将每个组压入栈中。在压入栈之前，我们需要判断rate是否呈递增的，若是呈递增的，那么直接要入栈中，因为我们可以两个分组取不同的rate；若不是呈递增，那么我们需要将最后一个组出栈，然后合并，因为我们要保证bi的呈递增的；然后判断这个新的组入栈是否能是栈呈递增，不能则重复前面的动作，直到呈递增或者栈为空为止，之后将新的组压入栈中。

最后得到一个递增的栈，我们直到了每个分组的rate值，那么就能求∑(bi-ai)^2了。

13197281	2015-03-21 16:21:03	Accepted	4923	1638MS	2408K	2440 B	C++	czy
13197275	2015-03-21 16:20:38	Time Limit Exceeded	4923	6000MS	2468K	2440 B	G++	czy

 #include <cstdio>
 #include <cstring>
 #include <stack>
 #include <vector>
 #include <algorithm>

 #define ll long long
 int const N = ;
 int const M = ;
 int const inf = ;
 ll const mod = ;

 using namespace std;

 int n;
 double ans;
 int aa[N];
 int a[N];
 int tot;
 ll qcnt1[N];
 ll qcnt[N];
 int T;

 void ini()
 {
     ans=;
     tot=;
     int i,j;
     int st,en;
     scanf("%d",&n);
     for(i=;i<=n;i++){
         scanf("%d",&aa[i]);
     }
     st=;
     while(st<=n){
         if(aa[st]==){
             st++;
         }
         else{
             break;
         }
     }
     if(st==n+) return;
     en=n;
     while(en>st){
         if(aa[en]==){
             en--;
         }
         else{
             break;
         }
     }
     j=;
     for(i=st;i<=en;i++){
         j++;
         a[j]=aa[i];
     }
     tot=j;
     //printf(" tot=%d\n",tot);
 }

 void solve()
 {
     int r;
     r=;
     ll cnt1,cnt0;
     ll cnt;
     int i;
     int now=;
     cnt1=cnt0=;
     for(i=;i<=tot;i++){
         if(now==){
             if(a[i]==){
                 cnt1++;
             }
             else{
                 cnt0++;
                 now=;
             }
         }
         else{
             if(a[i]==){
                 cnt0++;
             }
             else{
                 now=;
                 cnt=cnt0+cnt1;
                 while(r!= && qcnt1[r]*cnt > qcnt[r]*cnt1 ){
                     cnt1+=qcnt1[r];
                     cnt+=qcnt[r];
                     r--;
                 }
                 r++;
                 qcnt1[r]=cnt1;
                 qcnt[r]=cnt;
                 cnt0=;
                 cnt1=;
             }
         }
     }
     if(now==){
         cnt=cnt0+cnt1;
         while(r!= && qcnt1[r]*cnt > qcnt[r]*cnt1 ){
             cnt1+=qcnt1[r];
             cnt+=qcnt[r];
             r--;
         }
         r++;
         qcnt1[r]=cnt1;
         qcnt[r]=cnt;
     }
     double te;
     //printf("  r=%d\n",r);
     while(r!=){
         te=1.0*qcnt1[r]/qcnt[r];
         ans+=(-te)*(-te)*qcnt1[r]+te*te*(qcnt[r]-qcnt1[r]);
         r--;
     }
 }

 void out()
 {
     printf("%.6f\n",ans);
 }

 int main()
 {
     //freopen("data.in","r",stdin);
     scanf("%d",&T);
    // for(cnt=1;cnt<=T;cnt++)
     while(T--)
     //while(scanf("%d",&n)!=EOF)
     {
         ini();
         solve();
         out();
     }
 }