lucas定理证明

Lucas 定理（证明）

A、B是非负整数，p是质数。AB写成p进制：A=a[n]a[n-1]...a[0]，B=b[n]b[n-1]...b[0]。

则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0])  mod p 相同

即：Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)

证明：

首先我们注意到 n=(ak...a2,a1,a0)p  =  (ak...a2,a1)p * p + a0

=  [n/p]*p+a0

且m=[m/p]+b0

只要我们更够证明 C(n,m)=C([n/p],[m/p]) * C(a0,b0)  (mod p)

剩下的工作由归纳法即可完成

我们知道对任意质数p:   (1+x)^p  == 1+(x^p)  (mod p)

注意!这里一定要是质数。

（为什么要是质数呢？

因为(1+x)^p=1^p+c(p,1)x+c(p,2)x^2+...+x^p

但p为质数时c(p,1),c(p,2),...,c(p,p-1) 模p都为0

所以(1+x)^p == 1+x^p  (mod p)

）

对 模p 而言,接下来是让我惊叹的一个构造证明，证明只有一个公式如下：

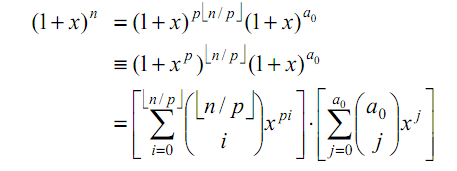
　　上式左右两边的x^m的系数对模p而言一定同余(为什么),其中左边的x^m的系数是 C(n,m) 而由于a0和b0都小于p

右边的x^m ( = x^(([m/p]*p)+b0)) 一定是由 x^([m/p]*p) 和 x^b0 相乘而得 (即发生于 i=[m/p] , j=b0 时) 因此我们就有了

C(n,m)=C([n/p],[m/p]) * C(a0,b0)  (mod p)

perfect！