hdu 1451 Area in Triangle(计算几何 三角形)
Given a triangle field and a rope of a certain length (Figure-1), you are required to use the rope to enclose a region within the field and make the region as large as possible.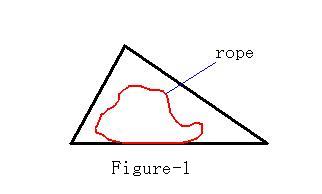
Output
题意:给你一个三角形的三个边,再给你一条长度为len的绳子.让你用绳子在三角形内圈出来一个区域让这个区域面积最大
思路:
我可以分类思考这个问题
1.如果绳子比三角形的周长还要长的话,最大的面积显然是这个三角形的面积
2.如果绳子很短呢?显然围成一个圆的时候面积是最大的.三角形里面最大的圆就是它的内切圆了
也就是说如果绳子的长度比三角形内切圆的周长还要小的时候,让它围成一个圆
3.当绳子介于1 2 的长度之间的呢?
当自由线从内切圆那种情况继续膨胀到能与三角形的边贴近但长度小于三角形周长时,将这个已经围成的面积划分为三个部分:
能构成一个更小的内切圆的三段弧,以三段弧的中心连结起来的一个更小且与原三角形相似的三角形,与原三角形贴近的三条边
所围成的三个矩形面积.

#include <bits/stdc++.h> using namespace std;
#define eps 1e-9
#define pi acos(-1.0)
#define zero(x) (((x)>0?(x):-(x))<eps)
double a,b,c,len;
int main()
{
//freopen("de.txt","r",stdin);
int casee = ;
while (~scanf("%lf%lf%lf%lf",&a,&b,&c,&len)){
//len为自由线的长度;p0为原三角形的周长;p1为原三角形的半周长;
//R为原三角形的内切圆半径;r为相似三角形的内切圆半径。
if (zero(a+b+c+len))
break;
printf("Case %d: ",++casee);
double p0 = a+b+c;
double p1 = p0/;
double S = sqrt(p1*(p1-a)*(p1-b)*(p1-c));
double R = *S/p0;//三角形内切圆公式S=p0*R/2; R为内切圆半径
if (len>=p0)
{
printf("%.2f\n",S);
continue;
}
else if (*pi*R-len>eps){
R = len/pi/;
S = pi*R*R;
printf("%.2f\n",S);
continue;
}
else{
double r = (p0-len)/(p0/R-*pi);
//利用的就是三角形相似的原理;公式;p0/R*(R-r)=len-2*pi*r;左边是通过内切圆半径与周长的关系求
//得小三角形的周长;右边是通过自由线的长度减掉三段弧得到相似三角形的周长;
double radio = (R-r)/R;//相似比
a*=radio;
b*=radio;
c*=radio;
double p=(a+b+c)/;
S = pi*r*r+sqrt(p*(p-a)*(p-b)*(p-c))+r**p;
printf("%.2f\n",S);
continue; }
}
return ;
}
hdu 1451 Area in Triangle(计算几何 三角形)的更多相关文章
- POJ 1927 Area in Triangle(计算几何)
Area in Triangle 博客原文地址:http://blog.csdn.net/xuechelingxiao/article/details/40707691 题目大意: 给你一个三角形的三 ...
- POJ 1927 Area in Triangle
Area in Triangle Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 1674 Accepted: 821 D ...
- hdu 2528:Area(计算几何,求线段与直线交点 + 求多边形面积)
Area Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
- hdu 2393:Higher Math(计算几何,水题)
Higher Math Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total ...
- hdu 4709:Herding(叉积求三角形面积+枚举)
Herding Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Sub ...
- hdu 2892 Area
http://acm.hdu.edu.cn/showproblem.php?pid=2892 解题思路: 求多边形与圆的相交的面积是多少. 以圆心为顶点,将多边形划分为n个三角形. 接下来就求出每个三 ...
- HDU 3007 Buried memory(计算几何の最小圆覆盖,模版题)
Problem Description Each person had do something foolish along with his or her growth.But,when he or ...
- POJ1927 Area in Triangle
Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 1458 Accepted: 759 Description Give ...
- 2018 ICPC Asia Singapore Regional A. Largest Triangle (计算几何)
题目链接:Kattis - largesttriangle Description Given \(N\) points on a \(2\)-dimensional space, determine ...
随机推荐
- http请求方法,get 对比 post
本文转自:http://www.w3school.com.cn/tags/html_ref_httpmethods.asp 两种最常用的 HTTP 方法是:GET 和 POST. 什么是 HTTP? ...
- python的final class
https://zhuanlan.zhihu.com/p/31674972 https://rainmanwy.github.io/Python的final-Class/
- Mac下用命令行压缩和解压rar文件的方法
废话不多说,直接进入主题 第一步:下载RAR工具包,根据自己需要下载相对应的版本 第二步:解压对应的压在的压缩包rarosx-5.4.0.tar.gz(我下载的是5.4.0版本) 第三步:从终端进入到 ...
- 传统神经网络ANN训练算法总结 参考 。 以后研究
http://blog.163.com/yuyang_tech/blog/static/21605008320146451352506/ 传统神经网络ANN训练算法总结 2014-07-04 17:1 ...
- Dapper - a simple object mapper for .Net
Dapper - a simple object mapper for .Net Release Notes Located at stackexchange.github.io/Dapper Pac ...
- Deepin 下开启SSH远程登陆
关于deepin下安装ssh以后root用户登陆报错的解决 最近刚刚接触到deepin,觉得,wow,除了mac,还有这么好看的非win系统,而且第测出那个Linux,宽容度很高,非常适合我这种比 ...
- seaborn教程4——分类数据可视化
https://segmentfault.com/a/1190000015310299 Seaborn学习大纲 seaborn的学习内容主要包含以下几个部分: 风格管理 绘图风格设置 颜色风格设置 绘 ...
- spring 配置属性细节
版权声明:本文为博主原创文章.未经博主同意不得转载. https://blog.csdn.net/qilixiang012/article/details/28233811 概要(红色为上一篇所讲,蓝 ...
- C#面试 笔试题 五
1.什么是受管制的代码? 答:unsafe:非托管代码.不经过CLR运行. 2.net Remoting 的工作原理是什么? 答:服务器端向客户端发送一个进程编号,一个程序域编号,以确定对象的位置. ...
- 参数化解决sql注入
用DynamicParameters: string where = " where a.is_deleted=0 and a.bvent_id=@bventId and au.user_t ...
