HDU 4812 (点分治)

题目：https://vjudge.net/contest/307753#problem/E

题意：给你一颗树，树上每个点都有个权值，现在问你是否存在 一条路径的乘积 mod 1e6+3  等于 k的路径，如果有找到字典序最小的方案

思路，树上路径~点分治    我们能知道每条路径的值，现在我们可以转化的问题是，怎么找一条路径等于K，和两条路径的乘积等于K,   首先第一种很明显就是判断相不相等即可，第二种的话，我们知道所有路径，我们怎么找到O(n)找到两个呢，我们用个数组存下所有是否出现过，然后，其实就是一个简单的小学问题，我们枚举每个距离的时候相当于 x,y,z已经知道 x,z了，式子是x*y=z，我们就只要判断z/x是否在标记数组中出现过即可，又因为这个有mod ,所以我们只能去乘z的逆元，这个时间卡的有点紧，我加了输入挂，和预处理逆元，map标记都不能用，只能用普通标记数组。

然后还有一个问题，你是否能和之前那样直接求出来所有的距离，答案是否定的，因为你直接去遍历数组标记，数组中的路径还含有两个都是同一子树的情况，这种时候是不能加入标记数组的，但是怎么避免呢，这里用到一个巧妙地方法，我们直接在计算所有路径到重心的距离的时候去更新答案，因为我们只有得到一个子树所有答案的时候才会存入标记数组，这样就避免一个子树的路径发生冲突的情况。最后我们再清空掉我们当前重心存入的答案。

还有更新答案的时候要注意的是，我们前面子树都保存的是点到重心的路径值，这里我们就不能也用点到重心的值了，因为就会多乘了一个重心节点的值，看下图

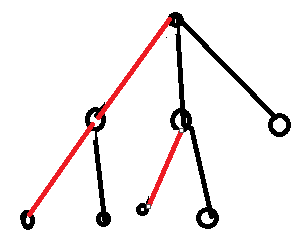
上面就是两条红色路径相乘就是两个路径合并起来了，主要还是因为这是点权，覆盖路径上所有点的点

#pragma comment(linker,"/STACK:102400000,102400000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<vector>
#include<map>
#define maxn 1000005
#define mod 1000003
#define MAX 0x3f3f3f
using namespace std;
typedef long long ll;
struct edge{
    int to,next;
}e1[*maxn];
ll da;
ll flag[maxn];
//vector<ll> mp[maxn];//存下图
bool vis[maxn];//标记曾经使用过的重心
ll maxsize[maxn],dis[maxn],d[maxn],last[maxn];//maxsize 当前节点的最大子树
ll siz[maxn],e[maxn],e2[maxn],id[maxn],wd[maxn],inv[maxn];// dis 到重心的距离  d 出现过的距离
ll n,m,rt,sum,qe,qe2,ans1,ans2,cnt;  // siz 当前节点的子树个数  e 出现的距离  rt代表当前重心
inline ll read()
{
    ll x=;char ch=getchar();
    while(ch<''||ch>'')ch=getchar();
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x;
}
void insert(int u,int v)
{
    e1[++cnt].to=v;e1[cnt].next=last[u];last[u]=cnt;
    e1[++cnt].to=u;e1[cnt].next=last[v];last[v]=cnt;
}
void find(ll x,ll f){//找出重心
    siz[x]=;
    maxsize[x]=;
    for(int i=last[x];i;i=e1[i].next){
        ll q=e1[i].to;
        if(q==f||vis[q]) continue;//vis数组标记曾经使用过的重心
        find(q,x);
        siz[x]+=siz[q];
        maxsize[x]=max(maxsize[x],siz[q]);
    }
    maxsize[x]=max(maxsize[x],sum-siz[x]);//节点总数减去当前的子树数=以当前节点为根的父亲点子树数
    if(maxsize[x]<maxsize[rt]){
        rt=x;
    }
}
void query(ll x,ll y){
    if(x>y) swap(x,y);
    if(x<ans1||(x==ans1&&y<ans2)){
        ans1=x;
        ans2=y;
    }
}
void get_dis(ll x,ll f,ll len,ll root){
    ll t=len%mod;
    if(t==m){//判断当前路径是否直接等于m
        query(root,x);
    }
    t=t*inv[wd[root]]%mod;//除去重心到子树那段距离，原因就是上述图
    ll t1=inv[t]*m%mod;
    e[++qe]=len%mod;
    e2[++qe2]=len%mod;//后面清空标记
    id[qe]=x;
    if(flag[t1]){//看是否另一条路径存在
        query(flag[t1],x);
    }
    for(int i=last[x];i;i=e1[i].next){
        ll q=e1[i].to;
        if(q==f||vis[q]) continue;
    //    dis[q]=(dis[x]*len)%mod;
        get_dis(q,x,(len*wd[q])%mod,root);
    }
}
void divide(ll x){
    //solve(x,wd[x]);
    qe2=;
    vis[x]=;
    for(int i=last[x];i;i=e1[i].next){
        ll q=e1[i].to;
        qe=;
        get_dis(q,x,wd[x]%mod*wd[q]%mod,x);
        for(int i=;i<=qe;i++){//记录当前的子树所有的距离
            if(flag[e[i]]==) flag[e[i]]=id[i];
            else flag[e[i]]=min(flag[e[i]],id[i]);
        }
    }
    for(int i=;i<=qe2;i++){//清空标记
        flag[e2[i]]=;
    }
    for(int i=last[x];i;i=e1[i].next){
        ll q=e1[i].to;
        if(vis[q]) continue;
        sum=siz[q];
        rt=;
        maxsize[rt]=MAX;
        find(q,x);
        divide(rt);
    }
}
void init(){
    for(int i=;i<=n;i++) last[i]=;
    for(int i=;i<=n;i++) vis[i]=;
    for(int i=;i<=n;i++) flag[i]=;
}
void pre(){
    cnt=;
    inv[] = inv[] = ;
    for (ll i = ; i < maxn; i++)
    inv[i] = (mod - mod / i)*inv[mod%i] % mod;
}
int main(){
    pre();
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        //if(n==0&&m==0) break;
        ll a,b,c;
        init();
        ans1=MAX;ans2=MAX;
        for(int i=;i<=n;i++) wd[i]=read();
         for(int i=;i<n;i++)
        {
            int u=read(),v=read();
            insert(u,v);
        }
        sum=n;//当前节点数
        rt=;
        maxsize[]=MAX;//置初值
        find(,);
        divide(rt);
        if(ans1!=MAX&&ans2!=MAX) printf("%lld %lld\n",ans1,ans2);
        else printf("No solution\n");
    }
}