Matlab——图形绘制——二维平面图形

二维平面图形

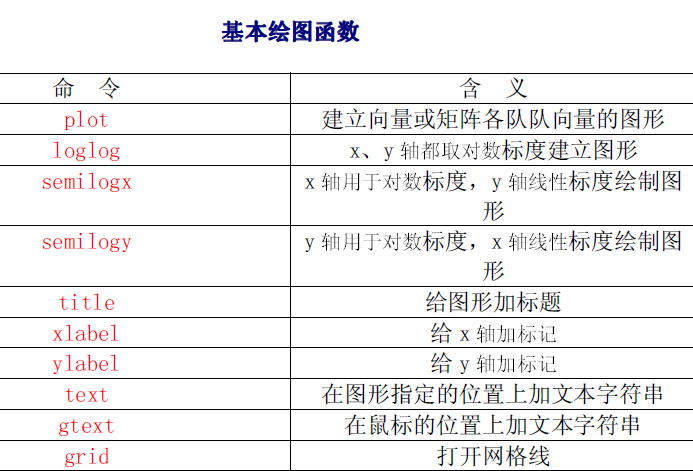
hold on ————在已画好的图形上添加新的图形

plot 是绘制一维曲线的基本函数，但在使用此函数之前，我们需先定义曲线上
每一点的x 及y 座标。下例可画出一条正弦曲线：

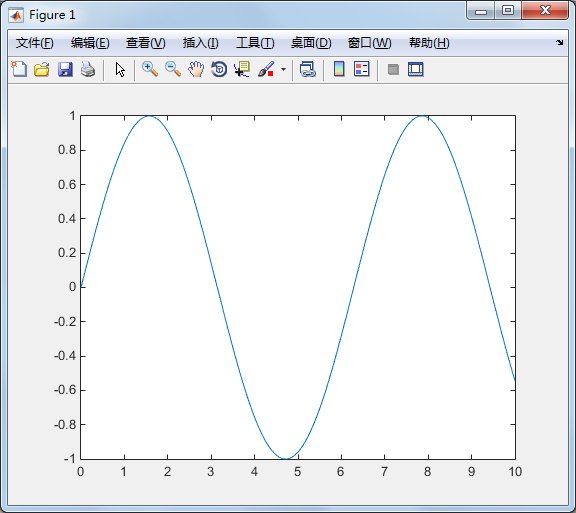
>> x=:0.001:; %  到10 的1000 个点的x 座标
y=sin(x); % 对应的y 座标
plot(x,y); % 绘图

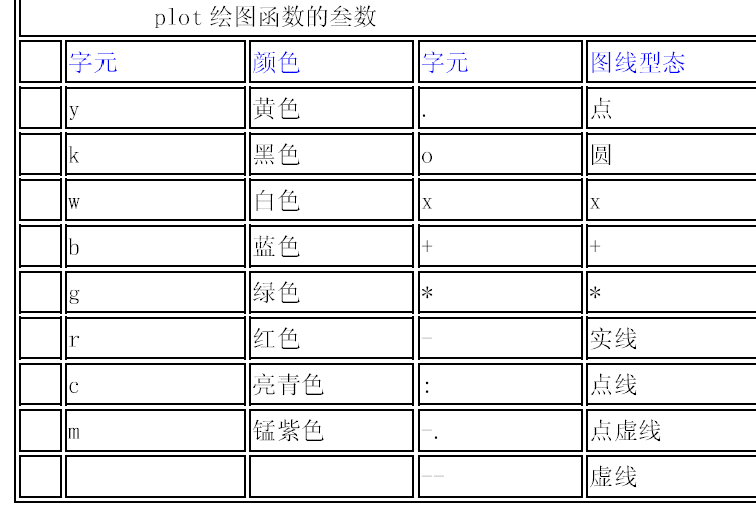
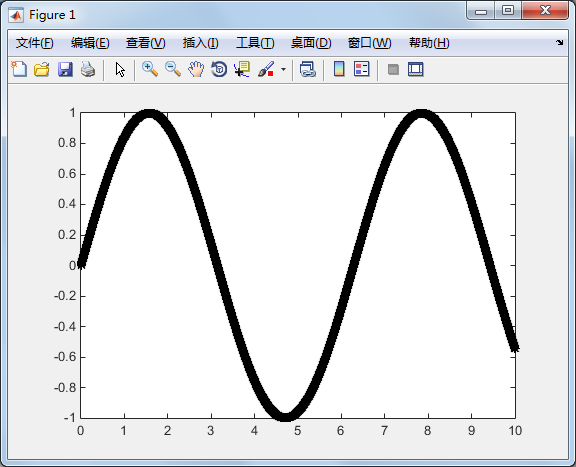
改变颜色

>> plot(x,y,'k')

改变颜色的同时改变图线形态

>> plot(x,y,'k*')

 同时画两个函数【淡粉色】

>> Y=sin(*x);
plot(x,y,'r:',x,Y,'b') % 同时画两个函数

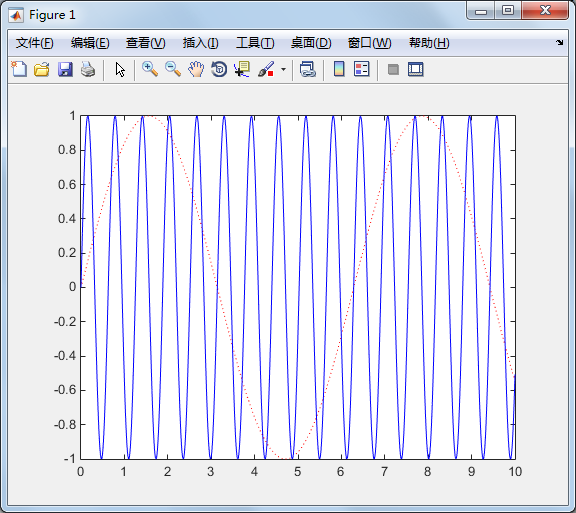
 调整图轴范围

>> axis([,,-,])   %前两个是横坐标，后两个是纵坐标

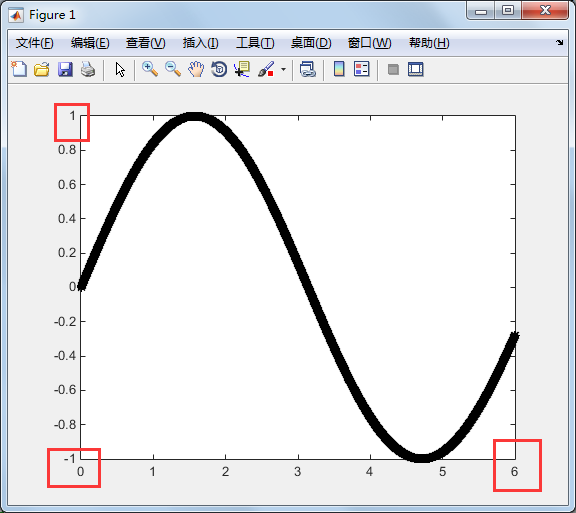
图形上加上注解

>> xlabel('x 轴'); % x 轴注解
ylabel('y 轴'); % y 轴注解
title('余弦函数'); % 图形标题
legend('y = cos(x)'); % 图形注解
gtext('y = cos(x)'); % 图形注解 ,用鼠标定位注解位置
grid on; % 显示格线

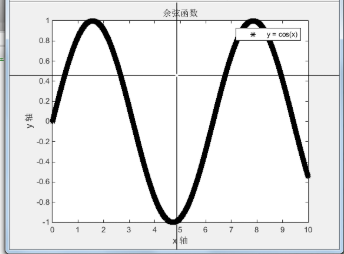
实例：将一函数 f(x)=sin(x)/x 在-20<x<20,-0.4<y<1.2 之间画出：

>> fplot('sin(x)./x',[-  -0.4 1.2])

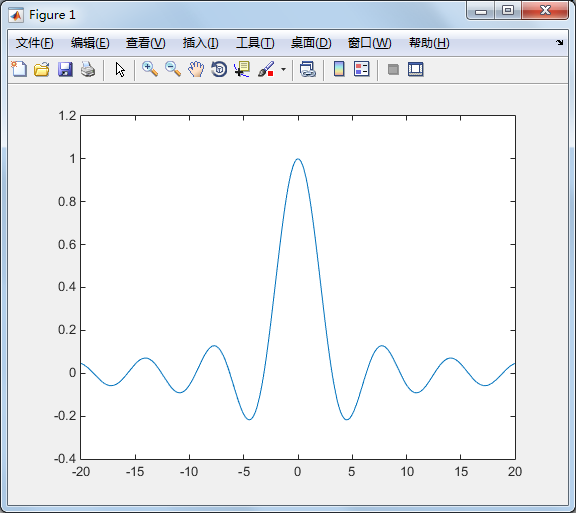
实例：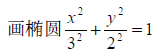

a = [:pi/:*pi]'; %角度 0 − 2p
X = cos(a)*; %参数方程
Y = sin(a)*;
plot(X,Y);
xlabel('x'), ylabel('y');
title('椭圆')

图形窗口的分割一般用命令subplot:

>> subplot(,,);
>> subplot(,,);

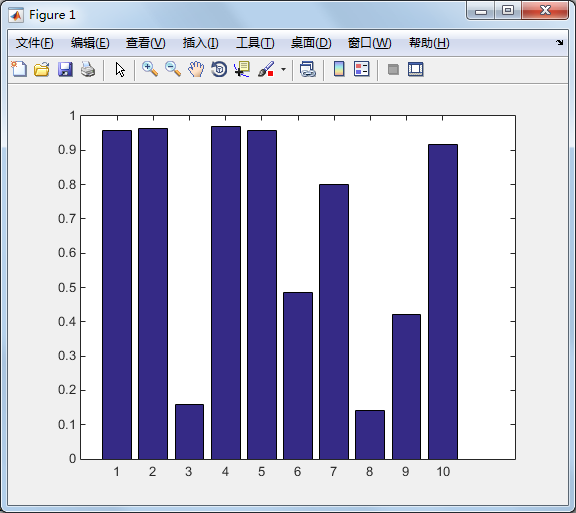
当资料点数量不多时——长条图

close all; %关闭所有的图形视窗
x=:;
y=rand(size(x));
bar(x,y);

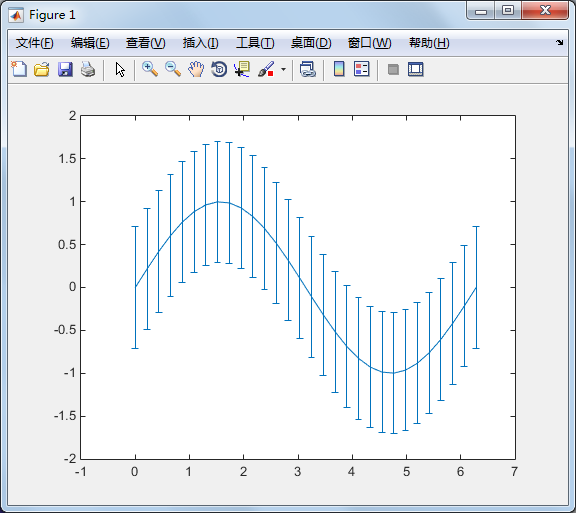
如果已知资料的误差量，就可用errorbar 来表示。下例以单位标准差来做资料
的误差量：

x = linspace(,*pi,);
y = sin(x);
e = std(y)*ones(size(x));
errorbar(x,y,e)

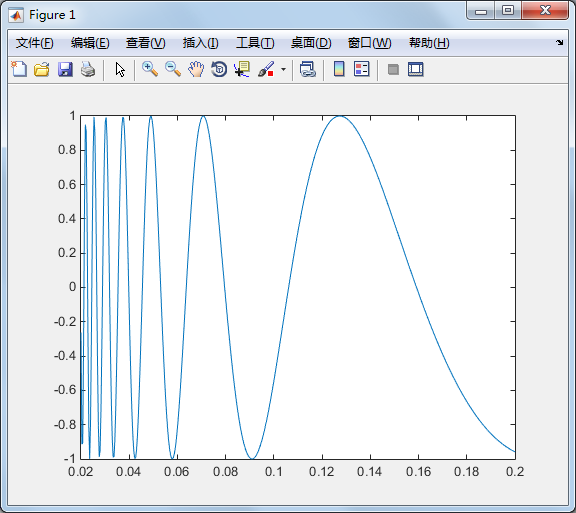
对於变化剧烈的函数，可用fplot 来进行较精确的绘图，会对剧烈变化处进行较
密集的取样，如下例：

>> fplot('sin(1/x)', [0.02 0.2]); % [0.02 0.2]是绘图范围

若要产生极座标图形，可用polar：

theta=linspace(, *pi);
r=cos(*theta);
polar(theta, r);

对於大量的资料，我们可用hist 来显示资料的分 情况和统计特性。下面几个
命令可用来验证randn 产生的高斯乱数分 ：

>> x=randn(, ); %产生5000个μ=，s=1的高斯乱数
>> hist(x,) %20代表长条的个数

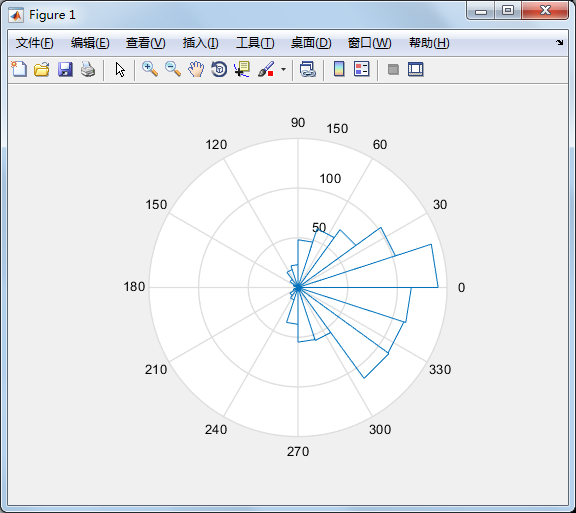
rose 和hist 很接近，只不过是将资料大小视为角度，资料个数视为距离，并用
极座标绘制表示：

x=randn(, );
rose(x);

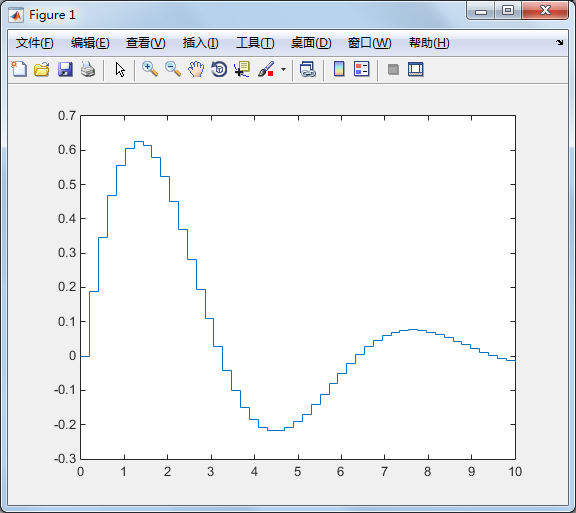
stairs 可画出阶梯图：

x=linspace(,,);
y=sin(x).*exp(-x/);
stairs(x,y);

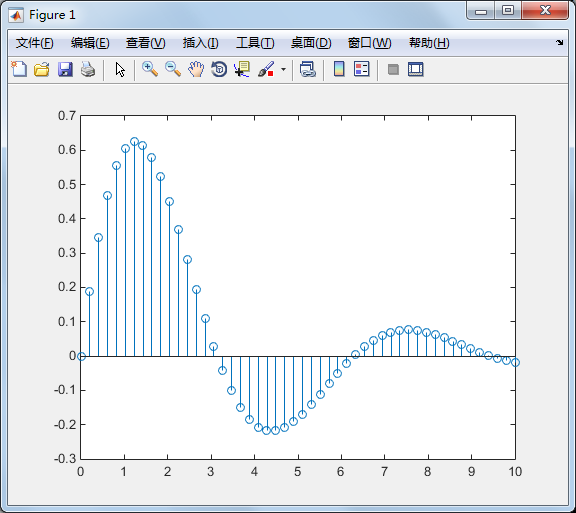
stems 可产生针状图，常被用来绘制数位讯号：

x=linspace(,,);
y=sin(x).*exp(-x/);
stem(x,y);

stairs 将资料点视为多边行顶点，并将此多边行涂上颜色：

>> x=linspace(,,);
y=sin(x).*exp(-x/);
fill(x,y,'b'); % 'b'为蓝色

feather 将每一个资料点视复数，并以箭号画出：

theta=linspace(, *pi, );
z = cos(theta)+i*sin(theta);
feather(z);

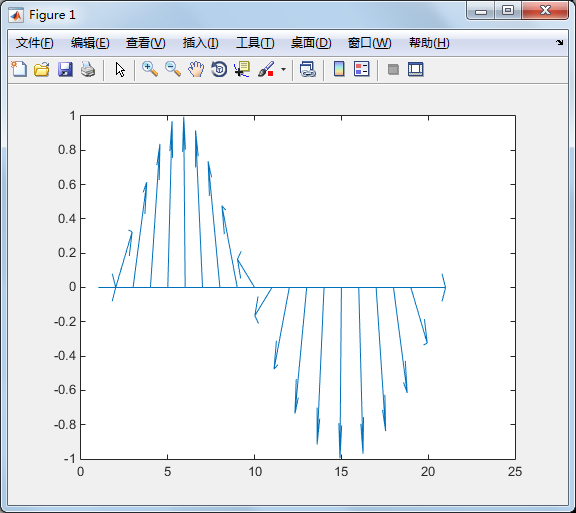
compass 和feather 很接近，只是每个箭号的起点都在圆点：

theta=linspace(, *pi, );
z = cos(theta)+i*sin(theta);
compass(z);