qbzt day2 上午

内容提要

贪心

分治

分块

搜索

---

接着昨天的讲

过河问题

考虑AB是最快的人，CD是最慢的人，要把CD两个人送过河，只有两种方案，牵扯到四个人，并且n个规模的原问题化成了n-2个规模的子问题

那么最后有两个情况，四个人和三个人，如果是四个人就直接按刚才的方法搞一搞就好了，如果是三个人的话，就有两个方案，一个是A来回送，一个是AB一起操作，就是在两个之间取min就好了

贪心算法在骗分时的运用主要集中在两点：

1.贪心算法失效时该如何补救？

2.如何利用贪心算法来提升自己的一个暴力算法？

1.贪心算法与随机化算法的结合（例如模拟退火）

在决策时有概率接受比当前情况差的方向

在搜索到结果时以一定概率跳出当前解，重新开始贪心

在贪心开始的时候，利用随机化选择多个起点开始贪心，取其最小值

2.贪心算法与搜索算法的结合

通过一定程度地选择次优解来计算答案,k-优搜索策略

结合贪心与搜索的策略，在大范围内贪心（用贪心剪枝），收束到小范围后开始搜索

分治：

分治分治，分而治之，分治算法就是将一个大问题划分为几个更小规模的问题并加以解决，通过解决子问题最后解决总问题。

分治算法在OI中的运用主要在两个方面：

1.基于二分查找、三分查找的运用

2.将题目划分为更细小的子问题的运用

我们将按顺序来讲解这两个方面

二分的本质是：在一个有序区间内确定一个边界，在边界的一边的元素满足某种性质，而另外一边不满足；

故二分经常用于解决如下类型的问题：

1.简单的二分查找

2.二分答案(即求一个单调函数在满足某个性质下的最值)

3.最值的最值(最常见的二分题类型)

差分前缀和加二分

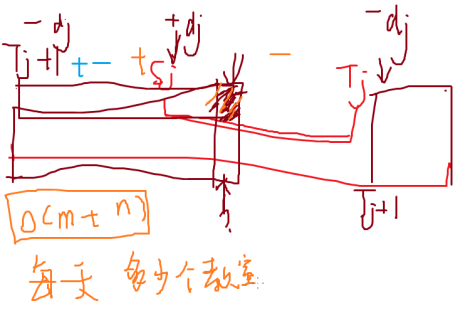
你现在需要给小A CntA 个自然数，给小B CntB 个自然数

但是给小A的自然数不能被x整除

同理给小B的自然数不能被y整除

请问需要给的最大的那个自然数最小是多少？

二分答案 v ，因为 a 不要被 x 整除的数，所以我们可以

先把 被 x 整除的数但不被 y 整除 给b，

再把 被 y 整除的数但不被 x 整除 给a。

然后剔除所有被 x*y 整除的数

剩下的数与 x 和 y 都互素，判一下能不能好好的分配就可以

三分

三分的难度要略低于二分(因为变出来的花样少)

三分的用处在于求一个单峰函数的最值

单峰函数，例如：

代码

如果函数不是单峰的该怎么办？

分块

分块算法相当于是一个对于线段树和树状数组算法的下位替代品

由于其算法简单粗暴十分好写故广泛地运用于骗分领域（滑稽

1.给出一个长度为n的数列，以及m个操作，支持区间加法，单点查询

把长为n的数组分成√n块，对其中某一个区间[l,r]进行修改

1. l和r在同一块里    直接跑，复杂度不超过√n
2. l和r在相邻的块里    直接跑，复杂度不超过2√n
3. 其他情况    把l和r所在的块暴力增加，对中间的块打标记，复杂度不超过3√n

2. 给出一个长为n的数列以及m个操作，支持区间加法，并询问区间内小于等于某个数x的元素个数

　　每个块内部排序

1. l和r在同一块里    直接跑√n
2. l和r在相邻的块里    直接跑 2√n
3. 其他情况    两边暴力中间二分√n logn+2√n

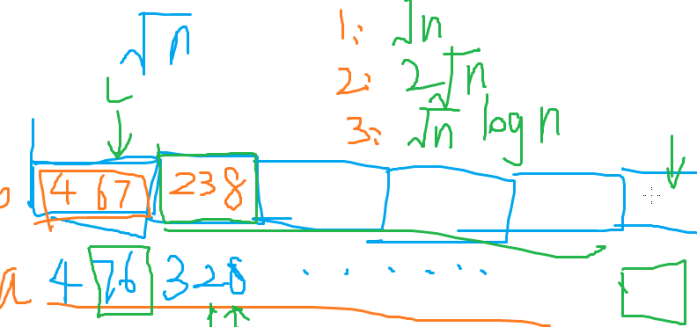
3. 给出一个长为n的数列以及m个操作，支持区间开方，区间求和

我们发现一个longlong范围的数最多六次开方就会变成0或1

我们如果某个区间里每个数都是0或1就不用管他了

复杂度o(n√n+6n)

记录color[i]表示下标为i的球的颜色

Pre[i]表示前一个颜色为color[i]的球的颜色（前一个颜色和i相同的球）

引理：

如果Pre[i]<x<i，那么[x,i]区间内只有一种颜色为color[i]的球

所以：

查询[l,r]中有多少不同的颜色

只需要查询[l,r]种所有pre[i]<l的i的个数

对于修改，只需要对每一种颜色开一个set，修改的时候用类似于链表的方式将后驱的pre指向前驱就好了

或者暴力改也可以qwq这个题修改比较水、

搜索

DFS

深搜，电风扇，大法师，回溯

是自己欺骗自己的好东西（滑稽）

较多用于走迷宫和树的遍历中（以及大名鼎鼎的网络爬虫）

虽然要利用栈进行递归但是不可思议地空间依旧比广搜小

一般结合强力的剪枝服用时有奇效

由于不需要搜索完所有的节点也能出一些结果，故在骗分界有广泛的好评

在寻找最优解的问题上基本被广搜吊打

BFS

杀人放火，居家常备，解决最优性问题有两把刷子

擅长答案在搜索树比较浅的位置时的情况

虽然名字叫广度优先搜索，但其实并不喜欢很宽的搜索树

状态的表示并没有深搜来的舒服

并没有很好的剪枝策略，垃圾节点一大堆

空间上完全被锤爆了，可以说是一点都没有考虑过内存的想法

最优解：广搜

T成狗：深搜

解个数：深搜

双向广搜

当你知道起点和终点时就可以使用的操作

能大大减少广搜扩展到垃圾节点

不过就算这样内存依旧表示很不友好

总的一句话，比广搜只好不差（当然代码量除外）

其实是有双向深搜和双向A*的，可是姿势太骚闪了自己的腰，并木有什么卵用

迭代加深搜索

算是广搜向内存妥协后的奇葩产物

先枚举深度，再dfs

骚气的结合了广搜和深搜的特点

和第一眼给人的逗比影响截然相反，迭代加深搜索在面对庞大的搜索树时往往表现出了值得信任的优异表现

能写出 more and more 骚气的操作

其实也是有迭代加宽搜索的，不过价值和他给人的第一印象一样不靠谱就是了

剪枝

常用的剪枝主要有以下几种：

可行性剪枝

最优性剪枝

记忆化搜索

搜索顺序以及代码细节

启发式剪枝

其实做题时想不想得到全靠脑洞，有没有效果全看缘分

剪枝一：如果在搜索的过程中体积小于0 或者当前半径或高度小于剩余要制作的层数（因为每层必须是相差1的，当前半径或高度小于要制作的层数，肯定不能制作完）就要剪枝.

剪枝二：当前剩下m层需要制作，可以预测制作这m层蛋糕最少需要多少体积，如果这个最少的体积还大于当前剩余的体积，那个这个不必继续搜索，所以要剪枝。

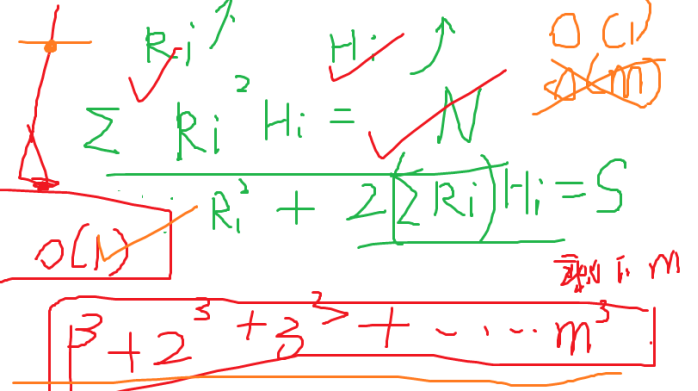
剪枝三：因为要求求最小表面积，如果当前枚举到的面积已经大于要求得的最优表面积，就要剪枝，但是这个剪枝还可以更优化，根据剪枝二的启发，如果当前枚举到的面积加上制作剩余m层蛋糕所要花费的最小表面积大于已经求得的最优解，那么剪枝。

剪枝四：因为体积必须为N，根据剪枝二，如果剩下m层蛋糕制作都按照最大的来，依然不能够使用完剩余的体积那么也要减掉。