[CSP-S模拟测试]:最大值（数学+线段树）

题目背景

　　$Maxtir$最喜欢最大值。

---

题目传送门（内部题128）

---

输入格式

　　第$1$行输入四个正整数$n,m,q$。
　　第$2$至$n+1$行中，第$i+1$行输入魔法晶石$i$的三种属性$(x_i,y_i,p_i)$。
　　接下来$q$行，每行两个正整数$l_i,r_i$，数据保证$[l_i,r_i]$互不包含。

---

输出格式

　　输出一行一个正整数$ans$表示答案。

---

样例

样例输入：

3 3 2
1 1 500000004
2 2 333333336
3 3 1
1 2
2 3

样例输出：

4

---

数据范围与提示

样例解释：

$500000004\equiv\frac{1}{2}\mod(10^9+7),333333336\equiv\frac{1}{2}\mod(10^9+7)$

最终的魔法阵中的晶石序列可能是

$(\otimes,\otimes,3),(\otimes,2,3),(1,\otimes,3),(1,2,3)$四种，他们的概率分别是$\frac{1}{3},\frac{1}{6},\frac{1}{3},\frac{1}{6}$

两次吸取的能量分别是$(0,3),(2,3),(1,3),(2,3)$，最终的答案是$3\times\frac{1}{3}+5\times\frac{1}{6}+4\times\frac{1}{3}+5\times\frac{1}{6}=4$

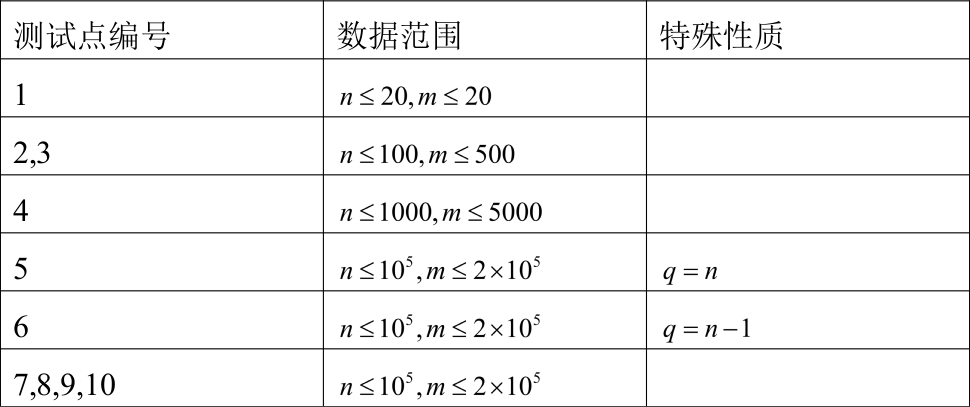
数据范围：

对于$100\%$的数据，满足$0\leqslant y_i\leqslant 10^9,1\leqslant q\leqslant n,0\leqslant p_i<10^9+7$

---

题解

先从$30\%$的部分分入手（$10\%$的暴力真的没什么技术含量）。

因为每个魔法阵要取最小值，所以不妨将魔法晶石从大到小排序。

一个魔法晶石能做贡献当且仅当它出现且比它小的都没有出现（当前魔法阵）。

所以考虑这种状态出现的概率，也就是求$P(\max\limits_{i=l}^rv_i\geqslant x)$；化一下式子，即可得到$1-\prod\limits_{i=l}^r1-P(v_i\geqslant x)$。

所以我们可以把小于$x$的数不选的概率乘起来再减去所有数都不选的概率，即$P(v_i\geqslant x)$。

考虑怎么优化，每次更改的贡献就是$1-P(v_i\geqslant y)\rightarrow 1-P(v_i\geqslant x)$。

但是我们可以只考虑$q=\prod\limits_{i=l}^r1-P(v_i\geqslant x)$，这样就可以$\Theta(\log n)$修改了。

想办法利用性质区间互不包含。

将所有区间按左端点排序，就可以实现点和区间的转化了利用线段树优化即可。

时间复杂度：$\Theta(m\log q)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const int mod=1000000007;
struct rec{int x,y,p;}f[200001];
struct node{int nxt,to;}e[400001];
int head[200001],cnt;
int n,m,q;
int l[200001],r[200001];
long long b[200001];
long long tr[400001],lz[400001];
pair<int,int> p[200001];
long long ans;
bool cmp(rec a,rec b){return a.y<b.y;}
void add(int x,int p)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=1LL*e[head[x]].to*(1-p)%mod;
	head[x]=cnt;
}
long long qpow(long long x,long long y)
{
	long long res=1;
	while(y)
	{
		if(y&1)res=res*x%mod;
		x=x*x%mod;y>>=1;
	}
	return res;
}
void pushup(int x){tr[x]=(tr[L(x)]+tr[R(x)])%mod;}
void build(int x,int l,int r)
{
	lz[x]=1;
	if(l==r){tr[x]=1;return;}
	int mid=(l+r)>>1;
	build(L(x),l,mid);
	build(R(x),mid+1,r);
	pushup(x);
}
void pushdown(int x)
{
	tr[L(x)]=lz[x]*tr[L(x)]%mod;
	tr[R(x)]=lz[x]*tr[R(x)]%mod;
	lz[L(x)]=lz[x]*lz[L(x)]%mod;
	lz[R(x)]=lz[x]*lz[R(x)]%mod;
	lz[x]=1;
}
void change(int x,int l,int r,int L,int R,int w)
{
	if(r<L||R<l)return;
	if(L<=l&&r<=R){tr[x]=tr[x]*w%mod;lz[x]=lz[x]*w%mod;return;}
	int mid=(l+r)>>1;
	pushdown(x);
	change(L(x),l,mid,L,R,w);
	change(R(x),mid+1,r,L,R,w);
	pushup(x);
}
void change(int x)
{
	if(r[x]<l[x])return;
	int res=qpow(1-(e[head[x]].to-b[x])%mod,mod-2);
	head[x]=e[head[x]].nxt;
	change(1,1,q,l[x],r[x],(1-e[head[x]].to+b[x])*res%mod);
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=m;i++)scanf("%d%d%d",&f[i].x,&f[i].y,&f[i].p);
	for(int i=1;i<=q;i++)scanf("%d%d",&p[i].first,&p[i].second);
	sort(f+1,f+m+1,cmp);cnt=n;
	for(int i=1;i<=n;i++){e[i].to=1;head[i]=i;}
	for(int i=1;i<=m;i++)add(f[i].x,f[i].p);
	for(int i=1;i<=n;i++)b[i]=e[head[i]].to;
	int fl=1,fr=0;
	for(int i=1;i<=n;i++)
	{
		while(fl<=fr&&p[fl].second<i)fl++;
		while(p[fr+1].first<=i&&fr<q)fr++;
		l[i]=fl;r[i]=fr;
	}
	build(1,1,q);
	for(int i=m,j;i;i=j)
	{
		for(j=i;f[i].y==f[j].y&&j;j--)change(f[j].x);
		ans=(ans+tr[1]*(f[i].y-f[j].y))%mod;
	}
	ans=(1LL*f[m].y*q-ans)%mod;
	printf("%d\n",(ans+mod)%mod);
	return 0;
}

---

rp++