Libre OJ 2255 （线段树优化建图+Tarjan缩点+DP）

题面

传送门

分析

主体思路：若x能引爆y,从x向y连一条有向边，最后的答案就是从x出发能够到达的点的个数

首先我们发现一个炸弹可以波及到的范围一定是坐标轴上的一段连续区间

我们可以用二分查找求出炸弹能波及到最左边和最右边的点，记为[l,r]

然后我们就需要向编号属于区间[l,r]的点连一条有向边

如果直接连边，时间复杂度为\(O(n^2)\) 无法接受，考虑用线段树优化连边

我们将线段树看成一个有向图，每个线段树节点看成图上的一个点，[l,r]向[l,mid],[mid+1,r]连边，叶子节点[l,l]向原图上的节点l连边

对于从x向编号属于区间[L,R]的点连边，我们用类似线段树区间更新的方法，将[L,R]拆成许多个小区间，再直接向这些小区间暴力连边



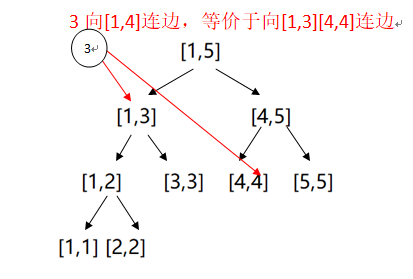
根据线段树的性质，最多会分出\(\left[ \log _{2}n\right]\)个节点，所以单次连边的时间复杂度为\(O(\log n)\)

然后就很套路了，显然环上的点可以缩成一个大点（权值为环上所有节点权值之和（线段树节点权值为0，原图上节点权值为1））

Tarjan完在DAG上DP即可

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<stack>
#include<queue>
#include<vector>
#define maxn 1700005
#define mod 1000000007
using namespace std;
inline void qread(int &x) {
	x=0;
	int sign=1;
	char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-') sign=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0';
		c=getchar();
	}
	x=x*sign;
}
inline void qread(long long &x) {
	x=0;
	long long sign=1;
	char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-') sign=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0';
		c=getchar();
	}
	x=x*sign;
}

int n;
long long x[maxn];
long long r[maxn];

struct edge {
	int from;
	int to;
	edge() {

	}
	edge(int u,int v) {
		from=u;
		to=v;
	}
	friend bool operator == (edge a,edge b) {
		return a.to==b.to&&a.from==b.from;
	}
	friend bool operator < (edge a,edge b) {
		if(a.from==b.from) return a.to<b.to;
		else return a.from<b.from;
	}
};
set<edge>vis1;
set<edge>vis2;
vector<int>G[maxn],D[maxn];
int w[maxn];
void add_edge(int u,int v) {
	G[u].push_back(v);
}

int newn=n;
struct node {
	int l;
	int r;
} tree[maxn];
void build(int l,int r,int pos) {
	newn++;
	tree[pos].l=l;
	tree[pos].r=r;
	if(l==r) {
		add_edge(pos+n,l);
		return;
	}
	add_edge(pos+n,pos*2+n);
	add_edge(pos+n,pos*2+1+n);
	int mid=(l+r)>>1;
	build(l,mid,pos<<1);
	build(mid+1,r,pos<<1|1);
}
void update(int L,int R,int v,int pos) {
	if(L<=tree[pos].l&&R>=tree[pos].r) {
		add_edge(v,pos+n);
		return;
	}
	int mid=(tree[pos].l+tree[pos].r)>>1;
	if(L<=mid) update(L,R,v,pos<<1);
	if(R>mid) update(L,R,v,pos<<1|1);
}

stack<int>s;
int tim=0;
int m=0;
int ins[maxn];
int dfn[maxn];
int low[maxn];
int belong[maxn];
int sz[maxn];
void tarjan(int x) {
	s.push(x);
	ins[x]=1;
	dfn[x]=low[x]=++tim;
	int tmp=G[x].size();
	for(int i=0; i<tmp; i++) {
		int y=G[x][i];
		if(!dfn[y]) {
			tarjan(y);
			low[x]=min(low[x],low[y]);
		} else if(ins[y]) {
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(low[x]==dfn[x]) {
		m++;
		int y;
		do {
			y=s.top();
			s.pop();
			ins[y]=0;
			belong[y]=m;
			sz[m]+=w[y];
		} while(x!=y);
	}
}

void dcg_to_dag() {
	for(int i=1; i<=n; i++) {
		if(!dfn[i]) tarjan(i);
	}
	int s;
	for(int i=1; i<=n; i++) {
		s=G[i].size();
		for(int j=0; j<s; j++) {
			if(belong[i]!=belong[G[i][j]]&&!vis2.count(edge(belong[i],belong[G[i][j]]))) {
				vis2.insert(edge(belong[i],belong[G[i][j]]));
				D[belong[i]].push_back(belong[G[i][j]]);
			}
		}
	}
}

long long dp[maxn];
int dfs(int x){
    if(dp[x]) return dp[x];
    dp[x]=sz[x];
    int tmp=D[x].size();
    for(int i=0;i<tmp;i++){
        int y=D[x][i];
        dp[x]+=dfs(y);
    }
    return dp[x];
} 

long long solve() {
	long long ans=0;
	for(int i=1;i<=n;i++){
		if(!dp[i]) dfs(i);
	}
	for(int i=1; i<=n; i++) {
		ans=(ans+w[i]*i*dp[belong[i]]%mod)%mod;
	}
	return ans;
}

int main() {
	int L,R;
	qread(n);
	for(int i=1; i<=n; i++) {
		w[i]=1;
		qread(x[i]);
		qread(r[i]);
	}
	newn=n;
	build(1,n,1);
	for(int i=1; i<=n; i++) {
		L=lower_bound(x+1,x+1+n,x[i]-r[i])-x;
		R=upper_bound(x+1,x+1+n,x[i]+r[i])-x-1;
		update(L,R,i,1);
	}
	n=newn;
	dcg_to_dag();
	printf("%lld\n",solve());
}