先行断言：

/a(?=b)/  ，positive lookahead，a的后方必须是b才行

/a(?!b)/   ，negative lookahead，a的后方必须不是b才能匹配

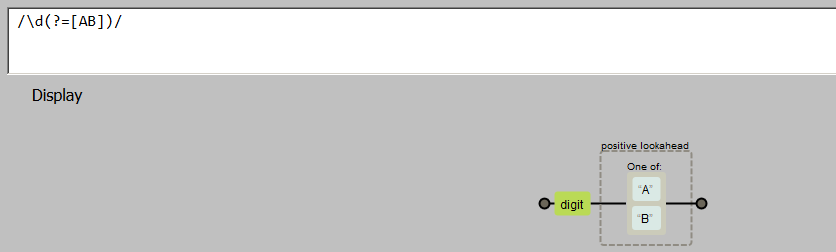
如下图示：  来自：https://regexper.com/#%2F%5Cd%28%3F%3D%5BAB%5D%29%2F

一个例子（转自：http://darkk6.blogspot.com/2017/03/regexp-lookahead-lookbehind.html

）

(?<!\d)\d{6,8}(?!\d)，來解釋看看這一段到底在找什麼東西。

先將其拆為：(?<!\d)　\d{6,8}　(?!\d) 三段，很快就可以看出，要找的東西是「6~8 個連續數字」，但是「前面不能有數字(Negative lookbehind)」以及「後面不能跟著數字(Negative lookahead)」。

由於 {6,8} 是贪心的 Greedy ，會盡量多取，因此就可以限制找到的數字數量是在 6~8 ，並且排除連續 9 個(以上)數字的部分了。

Regex: positive lookahead 先行断言____ 后行断言(lookbehind)的更多相关文章

  1. 正则表达式的先行断言(lookahead)和后行断言(lookbehind)

    正则表达式的先行断言和后行断言一共有4种形式: (?=pattern) 零宽正向先行断言(zero-width positive lookahead assertion) (?!pattern) 零宽 ...

  2. [转]正则表达式的先行断言(lookahead)和后行断言(lookbehind)

    正则表达式的先行断言和后行断言一共有4种形式: (?=pattern) 零宽正向先行断言(zero-width positive lookahead assertion) (?!pattern) 零宽 ...

  3. 转：正则表达式的先行断言(lookahead)和后行断言(lookbehind)

    正则表达式的先行断言和后行断言一共有4种形式: (?=pattern) 零宽正向先行断言(zero-width positive lookahead assertion) (?!pattern) 零宽 ...

  4. ErgExp-lookbehind assert(后行断言)

    //先行断言:先遇到一个条件,判断后面的条件是否满足 let test = 'hello world' console.log(test.match(/hello(?=\sworld)/)) //后行 ...

  5. 第11.20节 Python 中正则表达式的扩展功能：后视断言、后视取反

    一. 引言 在<第11.19节 Python 中正则表达式的扩展功能:前视断言和前视取反>中老猿介绍了前视断言和前视取反,与二者对应的还有后视断言和后视取反. 二. (?<=-)后视 ...

  6. 用fastreport在进行多列打印时，默认是先行后列，如何改成先列后行排记录？

    例子程序中的6.fr3是在Page中设置 columns=2这样就是先行后列,7.fr3就是3列先列后行的例子 1     6 2     7 3     8 4     9 5     10 但如果 ...

  7. python正则表达式--分组、后向引用、前(后)向断言

    无名.有名分组 (1)正则表达式—无名分组 从正则表 达式的左边开始看,看到的第一个左括号“(”表示表示第一个分组,第二个表示第二个分组, 依次类推. 需要注意的是,有一个隐含的全局分组(就是索引号为 ...

  8. jmeter接口测试-线程组设置(断言失败后用例停止执行)

    问题描述: jmeter跑接口用例的时候,其中一条用例的对断言失败后,后面的用例都不执行了! 解决思路1: 考虑应该有地方设置,在菜单栏找了半天没找到,百度也没有查到 解决思路2: jmeter源码导 ...

  9. python正则表达式(8)--分组、后向引用、前(后)向断言

    无名.有名分组 (1)正则表达式—无名分组 从正则表 达式的左边开始看,看到的第一个左括号“(”表示表示第一个分组,第二个表示第二个分组, 依次类推. 需要注意的是,有一个隐含的全局分组(就是索引号为 ...

随机推荐

  1. C#构造函数调用其他构造函数

    http://blog.csdn.net/dogfish/article/details/6990266  <-- 虏来的地 public class Class1 { public Class ...

  2. DP背包问题学习笔记及系列练习题

    01 背包: 01背包:在M件物品中取出若干件物品放到背包中,每件物品对应的体积v1,v2,v3,....对应的价值为w1,w2,w3,,,,,每件物品最多拿一件. 和很多DP题一样,对于每一个物品, ...

  3. JavaSE--java是值传递还是引用传递

    引用是已定义的变量的别名. 按引用传递就是一个变量使用两个名称. 两个变量在内存中的地址都是一样的. 按值传递, 传递的是值的拷贝. C++中可以通过传引用来改变传入的参数的值.在C++中可以通过以下 ...

  4. pytorch学习问题汇总

    问题六: 问题五:这里是怎么得到的? 问题四:为什么会是如下结果? torch.bernoulli(a)怎么是这个结果? 问题1:torch各个类型数据格式如何转换?数据类型在官方文档torch.Te ...

  5. C++的一些知识点汇总

    数组形参 数组形参 void test(const int arr[]); //arr中的值不能被改变 void test(const int *arr); //arr中的值不能被改变,包括arr[1 ...

  6. sql注入入门--基本命令

    本文转载自http://blog.csdn.net/zgyulongfei/article/details/41017493 本文仅献给想学习渗透测试的sqlmap小白,大牛请绕过. > > ...

  7. JavaScript 2019.3.15

    方法名.call(对象)可以切换方法调用的对象 参数数量 基本数据类型 typeof无法更细致的区分引用类型(全是object) =

  8. selenium请求豆瓣网

    #请求豆瓣网 from selenium import webdriverimport timedriver = webdriver.Chrome() driver.get("http:// ...

  9. 吴裕雄--天生自然C++语言学习笔记：C++简介

    C++ 是一种中级语言,它是由 Bjarne Stroustrup 于 年在贝尔实验室开始设计开发的.C++ 进一步扩充和完善了 C 语言,是一种面向对象的程序设计语言.C++ 可运行于多种平台上,如 ...

  10. 吴裕雄--天生自然 PHP开发学习：While 循环

    <html> <body> <?php $i=1; while($i<=5) { echo "The number is " . $i . &q ...