0-1背包问题-DP

中文理解：

0-1背包问题：有一个贼在偷窃一家商店时，发现有n件物品，第i件物品价值v_i元，重w_i磅，此处v_i与w_i都是整数。他希望带走的东西越值钱越好，但他的背包中至多只能装下W磅的东西，W为一整数。应该带走哪几样东西？这个问题之所以称为0-1背包，是因为每件物品或被带走；或被留下；小偷不能只带走某个物品的一部分或带走同一物品两次。

　　在分数（部分）背包问题（fractional knapsack problem)中，场景与上面问题一样，但是窃贼可以带走物品的一部分，而不必做出0-1的二分选择。可以把0-1背包问题的一件物品想象成一个金锭，而部分问题中的一件物品则更像金沙。

　　两种背包问题都具有最优子结构性质。对0-1背包问题，考虑重量不超过W而价值最高的装包方案。如果我们将商品j从此方案中删除，则剩余商品必须是重量不超过W-wj的价值最高的方案（小偷只能从不包括商品j的n-1个商品中选择拿走哪些）。

　　虽然两个问题相似，但我们用贪心策略可以求解背包问题，而不能求解0-1背包问题，为了求解部分数背包问题，我们首先计算每个商品的每磅价值v_i/w_{i。遵循贪心策略，小偷首先尽量多地拿走每磅价值最高的商品，如果该商品已全部拿走而背包未装满，他继续尽量多地拿走每磅价值第二高的商品，依次类推，直到达到重量上限W。因此，通过将商品按每磅价值排序，贪心算法的时间运行时间是O(nlgn)。}

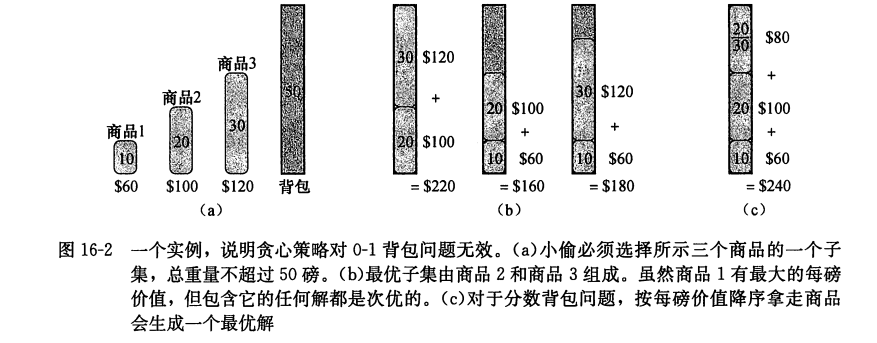
　　为了说明贪心这一贪心策略对0-1背包问题无效，考虑下图所示的问题实例。此例包含3个商品和一个能容纳50磅重量的背包。商品1重10磅，价值60美元。商品2重20磅，价值100美元。商品3重30磅，价值120美元。因此，商品1的每磅价值为6美元，高于商品2的每磅价值5美元和商品3的每磅价值4美元。因此，上述贪心策略会首先拿走商品1。但是，最优解应该是商品2和商品3，而留下商品1。拿走商品1的两种方案都是次优的。

　　但是，对于分数背包问题，上述贪心策略首先拿走商品1，是可以生成最优解的。拿走商品1的策略对0-1背包问题无效是因为小偷无法装满背包，空闲空间降低了方案的有效每磅价值。在0-1背包问题中，当我们考虑是否将一个商品装入背包时，必须比较包含此商品的子问题的解与不包含它的子问题的解，然后才能做出选择。这会导致大量的重叠子问题——动态规划的标识。

Knapsack Problem

The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.

It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items.

Example of a one-dimensional (constraint) knapsack problem: which boxes should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15 kg?

思路：

1.构建二维矩阵

2.找到最合适的项

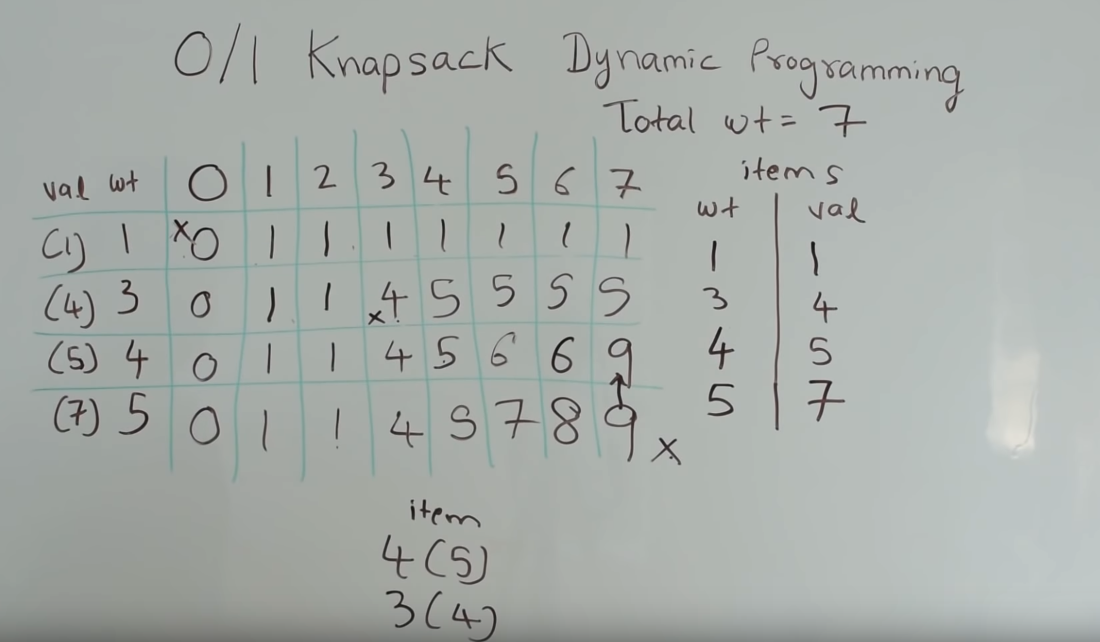
3.程序表示

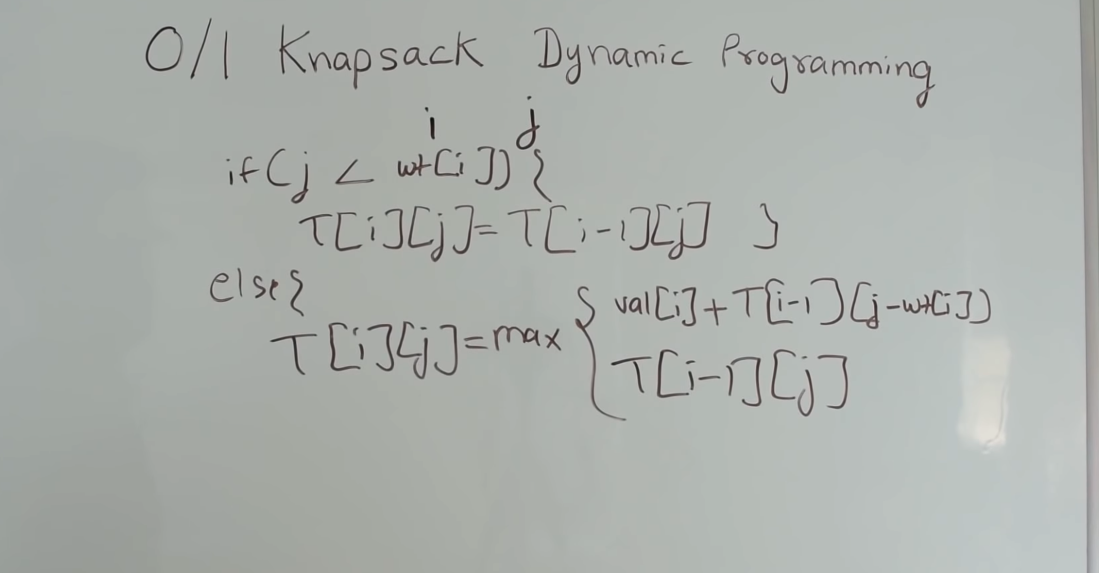
代码如下：

// Solve 0/1 knapsack problem
  // Dynamic Programming approach.
  solveZeroOneKnapsackProblem() {
    // We do two sorts because in case of equal weights but different values
    // we need to take the most valuable items first.
    this.sortPossibleItemsByValue();
    this.sortPossibleItemsByWeight();

    this.selectedItems = [];

    // Create knapsack values matrix.
    const numberOfRows = this.possibleItems.length;
    const numberOfColumns = this.weightLimit;
    const knapsackMatrix = Array(numberOfRows).fill(null).map(() => {
      return Array(numberOfColumns + ).fill(null);
    });

    // 初始化矩阵第一列
    for (let itemIndex = ; itemIndex < this.possibleItems.length; itemIndex += ) {
      knapsackMatrix[itemIndex][] = ;
    }

    //初始化矩阵第一行
    for (let weightIndex = ; weightIndex <= this.weightLimit; weightIndex += ) {
      const itemIndex = ;
      const itemWeight = this.possibleItems[itemIndex].weight;
      const itemValue = this.possibleItems[itemIndex].value;
      knapsackMatrix[itemIndex][weightIndex] = itemWeight <= weightIndex ? itemValue : ;
    }

    // Go through combinations of how we may add items to knapsack and
    // define what weight/value we would receive using Dynamic Programming
    // approach.
    for (let itemIndex = ; itemIndex < this.possibleItems.length; itemIndex += ) {
      for (let weightIndex = ; weightIndex <= this.weightLimit; weightIndex += ) {
        const currentItemWeight = this.possibleItems[itemIndex].weight;
        const currentItemValue = this.possibleItems[itemIndex].value;

        if (currentItemWeight > weightIndex) {
          knapsackMatrix[itemIndex][weightIndex] = knapsackMatrix[itemIndex - ][weightIndex];
        } else {
          // 考虑是否选择当前物品的重量与价值
          knapsackMatrix[itemIndex][weightIndex] = Math.max(
            currentItemValue + knapsackMatrix[itemIndex - ][weightIndex - currentItemWeight],
            knapsackMatrix[itemIndex - ][weightIndex],
          );
        }
      }
    }

    //对二维矩阵进行回溯，以确定相应的项------回溯这里的代码看不大懂
    let itemIndex = this.possibleItems.length - ;
    let weightIndex = this.weightLimit;

    while (itemIndex > ) {
      const currentItem = this.possibleItems[itemIndex];
      const prevItem = this.possibleItems[itemIndex - ];

      // Check if matrix value came from top (from previous item).
      // In this case this would mean that we need to include previous item
      // to the list of selected items.
      if (
        knapsackMatrix[itemIndex][weightIndex]
        && knapsackMatrix[itemIndex][weightIndex] === knapsackMatrix[itemIndex - ][weightIndex]
      ) {
        // Check if there are several items with the same weight but with the different values.
        // We need to add highest item in the matrix that is possible to get the highest value.
        const prevSumValue = knapsackMatrix[itemIndex - ][weightIndex];
        const prevPrevSumValue = knapsackMatrix[itemIndex - ][weightIndex];
        if (
          !prevSumValue
          || (prevSumValue && prevPrevSumValue !== prevSumValue)
        ) {
          this.selectedItems.push(prevItem);
        }
      } else if (knapsackMatrix[itemIndex - ][weightIndex - currentItem.weight]) {
        this.selectedItems.push(prevItem);
        weightIndex -= currentItem.weight;
      }

      itemIndex -= ;
    }
  }