Codeforces 1299B/1300D - Aerodynamic

题目大意：

给定一个图形S，让这个图形任意平移，但是要保证原点（0,0）一直在它的内部或者边上

最后把它能移动到的所有位置进行拼合可以得到一个图形T

问图形S与图形T是否相似

点会按照逆时针顺序给出

x和y都是整数

图1：图示正三角形平移后拼合可以得到一个正六边形

图2：斜正方形平移后拼合可以得到一个大的斜正方形

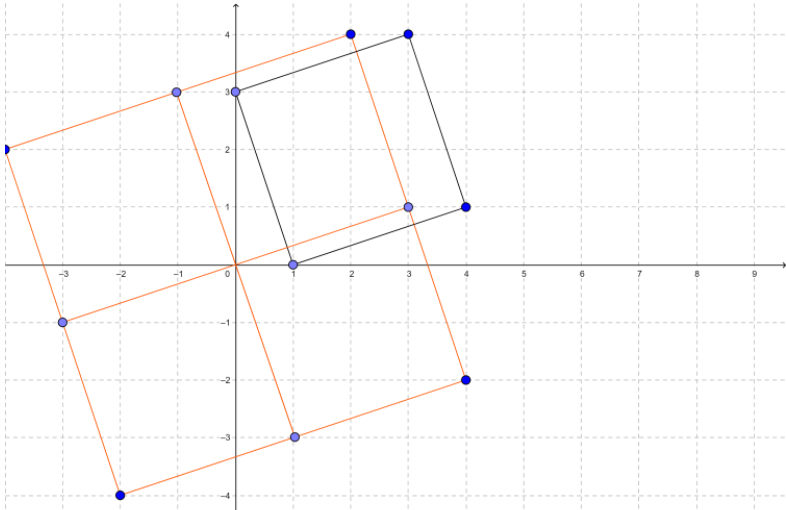
解题思路：

证：

首先能得到的结论是，不论给定的是什么图形，让他平移后得到的图形T绝对是一个中心对称图形（这个草稿纸上证明下吧，或者下面也会有证明）

所以要想让某个图形与一个中心对称图形对称，那么这个图形也必须是中心对称图形

那么就需要证明对于中心对称图形是否存在某种限制不符合题意

可以由中心对称图形的性质得到，假设图形上某条边为a，与这条边呈中心对称的另外一条边为b

那么一定会有|a|=|b|，且a//b

在根据题意进行平移之后，对应的边将会是当前边长+对称边边长和

又因为|a|=|b|，所以对应边会变成原来的两倍长，即a对应的边边长为|a|+|b|=2|a|，b对应边的边长为|b|+|a|=2|b|

即，中心对称图形进行平移后得到的图形T是原本的图形扩大2倍的结果，任何中心对称图形都满足题意

只要给定的图形S不是中心对称图形，首先，肯定存在一条边没有他的中心对称边（一定存在a找不到a//b的b）

那么当前位置平移后将会得到边长为|a|+0，对称的位置的边（在S中不存在的但是又要和a平行的那个位置，在T中存在）对应将会得到边长为0+|a|的边

所以可以证明得到图形T一定是中心对称图形

以不是中心对称的四边形为例，易得到上述结论：

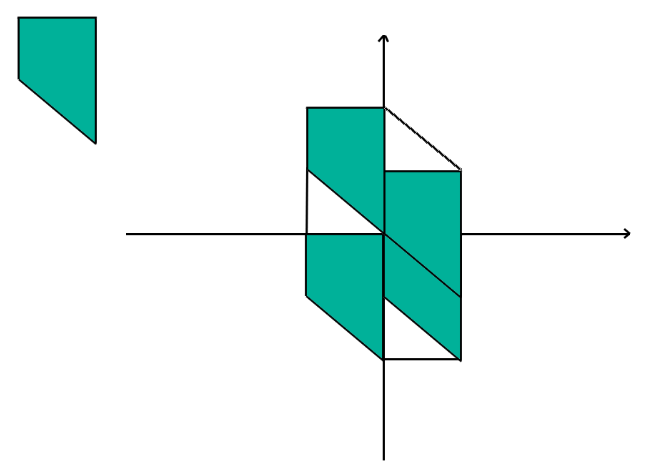
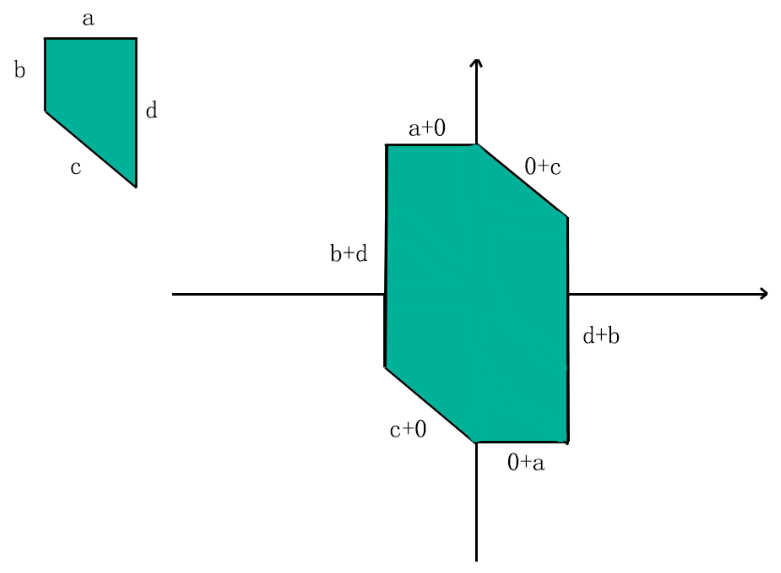
如图所示的是，因为a和c没有与其平行的对应边，所以会单独成两个对应边，长度为自身

因为b与d互为平行边，所以可以凑成两个长为b+d的对应边

解：

已经按照逆时针顺序给出，那判断就很容易了

首先，中心对称图形必须是偶数个点，所以n为奇数直接输出NO

然后，输入n个点，根据中心对称图形的性质，又因为点按照逆时针给出，可得

第1个点和第n/2+1个点

第2个点和第n/2+2个点

第3个点和第n/2+3个点

...

第n/2个点和第n个点

这些两点组合它们的线段会同时交于一点，且这个点也是它们线段的中点

根据这个性质，先记录下第1个点和第n/2+1个点组成线段的中点，就能知道这整个图形的中点(cx,cy)

接下来最多只需要再判断n/2-1组点对就能得出判断结果了

为了防止取中点时/2的误差，所以点要用double储存

正常情况下对于double计算精度问题需要用eps判断两点是否相等，但是由于这题给定的点是整数，/2后最坏情况只能拿到个.5的浮点部分，所以二进制储存是精确的，不需要加eps

代码1（717ms）：

#include<bits/stdc++.h>
using namespace std;
double x[],y[];
int main(){
    ios::sync_with_stdio();
    cin.tie();cout.tie();
    int n,i,j;
    double cx,cy,dx,dy;
    cin>>n;
    if(n&){
        cout<<"NO\n";
        return ;
    }
    for(i=;i<=n;i++)
        cin>>x[i]>>y[i];
    cx=(x[]+x[n/+])/2.0;
    cy=(y[]+y[n/+])/2.0;
    for(i=,j=n/+;j<=n;i++,j++){
        dx=(x[i]+x[j])/2.0;
        dy=(y[i]+y[j])/2.0;
        if(cx!=dx||cy!=dy){
            cout<<"NO\n";
            return ;
        }
    }
    cout<<"YES\n";

    return ;
}

发现这样耗时很大，所以要对计算进行优化

首先可以发现，所有计算中点的式子都有一个/2

如果把所有的/2都去掉，对答案的判断是不会变的

所以double此时也可以改成int了（两种类型计算方式不同时间差别很大）

因为点的最大值只有1e9，相加最大2e9，不会超出int范围，所以不需要开long long

然后，从读入入手，可以先读n/2+1个点，剩下的n/2-1个点边读入边判断（减少这中间的耗时，虽然也差不了多少）

代码2（109ms）：

#include<bits/stdc++.h>
using namespace std;
int x[],y[];
int main(){
    ios::sync_with_stdio();
    cin.tie();cout.tie();
    int n,i,j,cx2,cy2;
    cin>>n;
    if(n&){
        cout<<"NO\n";
        return ;
    }
    for(i=;i<=n/;i++)
        cin>>x[i]>>y[i];
    cin>>x[n/+]>>y[n/+];
    cx2=x[]+x[n/+];
    cy2=y[]+y[n/+];
    for(i=,j=n/+;j<=n;i++,j++){
        cin>>x[j]>>y[j];
        if(x[i]+x[j]!=cx2||y[i]+y[j]!=cy2){
            cout<<"NO\n";
            return ;
        }
    }
    cout<<"YES\n";

    return ;
}