2019.3.13 Java实现分数的四则运算

Java实现分数的四则运算

自己的写法

markdown太久没写格式不会用了--将就着看

• Fraction.java

package com.lanou;

public class Fraction {

    private int numerator1;     //定义属性:分子1
    private int denominator1;  //定义属性:分母1

    private String operator;      //定义属性:运算符

    private int numerator2;        //定义属性:分子2
    private int denominator2;       //定义属性:分母2

    //构造方法
    //constructor生成

    public Fraction(int numerator1, int denominator1, String operator, int numerator2, int denominator2) {
        this.numerator1 = numerator1;
        this.denominator1 = denominator1;
        this.operator = operator;
        this.numerator2 = numerator2;
        this.denominator2 = denominator2;
    }

    //加法
    public void addition() {

            int x = numerator1 * denominator2 + numerator2 * denominator1;
            int y = denominator1 * denominator2;
            gcd(x,y);

        }

    //减法
    public void subtraction() {

            int x = numerator1 * denominator2 - numerator2 * denominator1;
            int y = denominator1 * denominator2;
            gcd(x,y);
        }

    //乘法
    public void multiplication(){

        int x = numerator1 * numerator2;
        int y = denominator1 * denominator2;
        gcd(x,y);
    }

    //除法
    public void division(){

        int x = numerator1 * denominator2;
        int y = denominator1 * numerator2;
        gcd(x,y);

    }

    //欧几里得+判断输出
    public int gcd(int m,int n) {

        //定义四个空变量
        int r;
        int t;
        int u;
        int w;

        //t和w用来存储分子和分母的初始数据
        t = m;
        w = n;

        //求最大公因数
        while (n != 0) {
            r = m % n;
            m = n;
            n = r;
        }
        //循环结束后此时m即为最大公因数
        //放个u = m看着方便
        u = m;

        //分子分母分别除以最大公因数
        t = t / u;
        w = w / u;

        //判断+输出
        //分子分母都为1 直接输出1
        if(t == 1 && w == 1){

            System.out.println("1");
        }
        //分子为0 分母不为0 直接输出0
        else if(t == 0 && w != 0){

            System.out.println("0");
        }
        //分子分母都不为0且不为1 直接输出
        else {

            System.out.println(t + "/" + w);
        }

        return 0;

    }

}

• MainClass.java

package com.lanou;
import java.util.Scanner;

public class MainClass {

    public static void main(String[] args) {

        System.out.println("请输入按分子1分母1运算符分子2分母2的形式输入数据");
        Scanner scanner = new Scanner(System.in);

        int a = scanner.nextInt();
        int b = scanner.nextInt();
        String o = scanner.next();
        int c = scanner.nextInt();
        int d = scanner.nextInt();

        //判断分母是否为0 若为0重新输入 不为0继续判断
        if (b == 0 || d == 0){

            System.out.println("分母不能为零,请重新输入");

            a = scanner.nextInt();
            b = scanner.nextInt();
            o = scanner.next();
            c = scanner.nextInt();
            d = scanner.nextInt();
        }

        //判断o中是否是运算符
        if (!o.equals("+") && !o.equals("-") && !o.equals("*") && !o.equals("/")){

            System.out.println("运算符输入错误,请重新输入");

            a = scanner.nextInt();
            b = scanner.nextInt();
            o = scanner.next();
            c = scanner.nextInt();
            d = scanner.nextInt();
        }

        Fraction fraction = new Fraction(a, b, o, c, d);

        if (o.equals("+")){

            fraction.addition();
        }
        else if (o.equals("-")){

            fraction.subtraction();
        }
        else if (o.equals("*")){

            fraction.multiplication();
        }
        else if (o.equals("/")){

            fraction.division();
        }

    }
}

大仁哥的写法

/**
 * @author lizhongren1.

*/
public class Fraction {

    // 分子(numerator)

    private int ntNum;

    // 分母(Denominator)

    private int doNum;

// 构造方法, 这里没写空的构造方法, 换句话说就是要求必须要有分子和分母.

    public Fraction(int ntNum, int doNum) {

    this.ntNum = ntNum;

    this.doNum = doNum;

    if (doNum == 0){
                // 分母不能为0

    System.out.println("分母不能为0, 已经改为1");

    this.doNum = 1;
     }

        // 创建新分数之后进行约分处理

    reduce();
  }

// 分数加法

public Fraction add(Fraction f){

// a/b + c/d

// 生成新的分子: a * d + b * c

int newNt = ntNum * f.getDoNum() + doNum * f.getNtNum();

// 生成新的分母: b * d

int newDo = doNum * f.getDoNum();

// 使用新的分子分母创建一个新的分数对象

Fraction newF = new Fraction(newNt, newDo);

return newF;
    }

// 约分方法: 把分数化为最简分数, 即 6/12 化为 1/2

// 此方法和下一个方法都不想让外部调用, 因此设置为private

private void reduce(){

// 获得最大公约数

int m = maxDe(ntNum, doNum);

ntNum = ntNum / m;

doNum = doNum / m;
    }

// 最大公约数: 使用辗转相除法(又名欧几里德算法, 别问我怎么来的, 去问欧几里德)

private int maxDe(int a, int b){

while(b != 0)
        {

int r = a % b;

a = b;

b = r;

}

return a;

}

    // 输出字符串, 按照 分子/分母的形式输出

@Override

public String toString() {

// 分子为0时输出0

if (ntNum == 0){

return "0";

}

        // 分子分母相同时输出1

if (ntNum == doNum){

return "1";
        }

        // 其余方式按 分子/分母 输出

return ntNum + "/" + doNum;
    }

    // getter/setter方法

public int getNtNum() {

return ntNum;
    }

public void setNtNum(int ntNum) {

this.ntNum = ntNum;
    }

public int getDoNum() {

return doNum;
    }

public void setDoNum(int doNum) {

this.doNum = doNum;
    }

    // main方法测试

public static void main(String[] args) {

Fraction f1 = new Fraction(1,3);

Fraction f2 = new Fraction(4,9);

        // 分数f1 加上 分数f2

Fraction nf = f1.add(f2);

System.out.println(nf);

System.out.println(nf.add(new Fraction(9,12)));
    }
}

• 输入与输出

• 测试数据

• 输入格式:分子1 回车 分母1 回车 运算符 回车 分子2 回车 分母2 回车

• 1/4+1/4

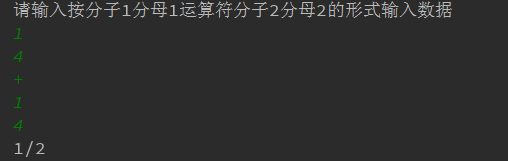
• 0/4+0/4

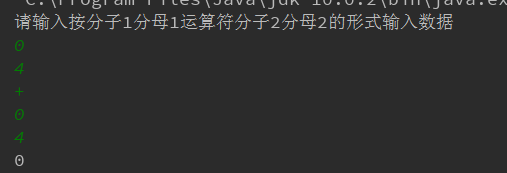
• 4/0+4/0