Pollard_Rho 整数分解法【学习笔记】

引文：如果要对比较大的整数分解，显然之前所学的筛选法和是试除法都将不再适用。所以我们需要学习速度更快的Pollard_Rho算法。

算法原理：

生成两个整数a和b，计算p=gcd(a-b, n)，知道p不为1或a,b出现循环为止，若p=n，则n为质数，否则p为n的一个约数。

对于如何生成这两个数，选取一个小的随机数x₁，迭代生成

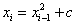
通过这个方式，我们只需要知道x₁和c就可以生成一系列数值，c可以取任意给定值，一般取c=1。

若序列出现循环，则退出。

计算p=gcd(x_i-1-x_i, n)， 若p=1，返回上一步，直到p>1为止；若p=n，则n为素数，否则p为一个约数并递归分解p和n/p。

例题：https://vjudge.net/problem/POJ-1811

 代码：

 #include <iostream>
 #include <cstdio>
 #include <fstream>
 #include <vector>
 #include <queue>
 #include <algorithm>
 #include <map>
 #include <cmath>

 using namespace std;
 typedef long long LL;
 const int Test[] = {, , , , , , , };
 const int Times = ;
 vector<LL> Factor;

 LL gcd(LL a, LL b)
 {
     return b==?a:gcd(b, a%b);
 }

 LL Multi(LL a, LL b, LL mod)
 {
     LL ans = ;
     while(b)
     {
         if(b&)
             ans = (ans + a)%mod;
         a = (a+a)%mod;
         b>>=;
     }
     return ans;
 }

 LL Pow(LL a, LL b, LL mod)
 {
     LL ans = ;
     while(b)
     {
         if(b&)
         {
             ans = Multi(ans, a, mod);
         }
         b>>=;
         a=Multi(a, a, mod);
     }
     return ans;
 }

 bool Miller_Rabin(LL n)
 {
     if(n < )   return false;
     LL s = n-, t = , x, next;
     while(!(s&) )  //根据运算符的优先级必须加括号
     {
         s>>=;
         t++;
     }
     for(int i = ; i < Times; i++)
     {
         if(n== Test[i]) return true;
         x = Pow(Test[i], s, n);
         for(int j = ; j <= t; j++)
         {
             next = Multi(x, x, n);
             if(next ==  && x !=  && x != n-)
                 return false;
             x = next;
         }
         if(x != )
             return false;
     }
     return true;
 }

 LL Pollard_Rho(LL n, int c)
 {
     LL i = , k = ;
     LL x = rand()%(n-) + , y; //保证随机数在(0,n)内
     y = x;
     while()
     {
         i++;
         x = (Multi(x, x, n) + c)%n;  //继续生成数
         LL p = gcd(x>y?x-y:y-x, n);
         if(p!= && p!=n)    //因为p>1
             return p;
         if(y == x)
             return n;
         if(i == k)
         {
             y = x;
             k<<=;
         }
     }
 }

 void Find(LL n, int c)
 {
     if(n == )
         return;
     if(Miller_Rabin(n))
     {
         Factor.push_back(n);
         return;
     }
     LL p = n, k = c;
     while(p >= n)
     {
         p = Pollard_Rho(n, c--);
     }
     Find(p, k);
     Find(n/p, k);
 }

 int main()
 {
     int T;
     LL x;
     cin >>T;
     while(T--)
     {
         Factor.clear();
         cin >> x;
         Find(x, );   //107足矣
         if(Factor.size() == )
             printf("Prime\n");
         else
         {
             sort(Factor.begin(), Factor.end());
             printf("%I64d\n", Factor[]);
         }
     }
 }

Code