洛谷 P3302 [SDOI2013]森林 Lebal：主席树 + 启发式合并 + LCA

题目描述

小Z有一片森林，含有N个节点，每个节点上都有一个非负整数作为权值。初始的时候，森林中有M条边。

小Z希望执行T个操作，操作有两类：

1. Q x y k查询点x到点y路径上所有的权值中，第k小的权值是多少。此操作保证点x和点y连通，同时这两个节点的路径上至少有k个点。
2. L x y在点x和点y之间连接一条边。保证完成此操作后，仍然是一片森林。

为了体现程序的在线性，我们把输入数据进行了加密。设lastans为程序上一次输出的结果，初始的时候lastans为0。

• 对于一个输入的操作Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。
• 对于一个输入的操作L x y，其真实操作为L x^lastans y^lastans。其中^运算符表示异或，等价于pascal中的xor运算符。

请写一个程序來帮助小Z完成这些操作。

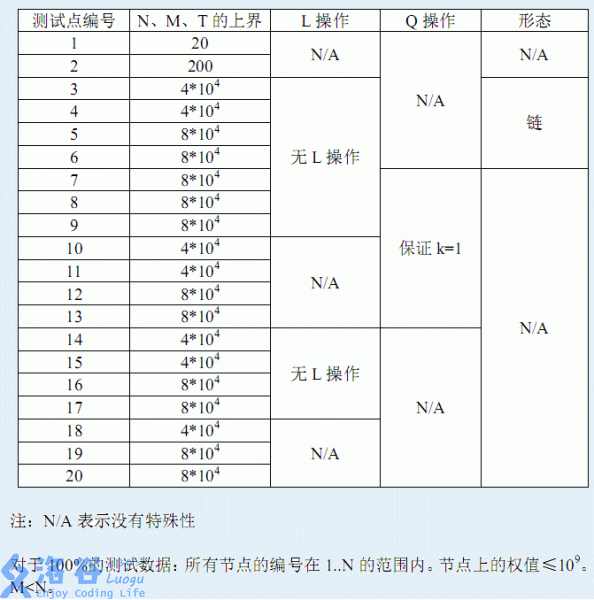
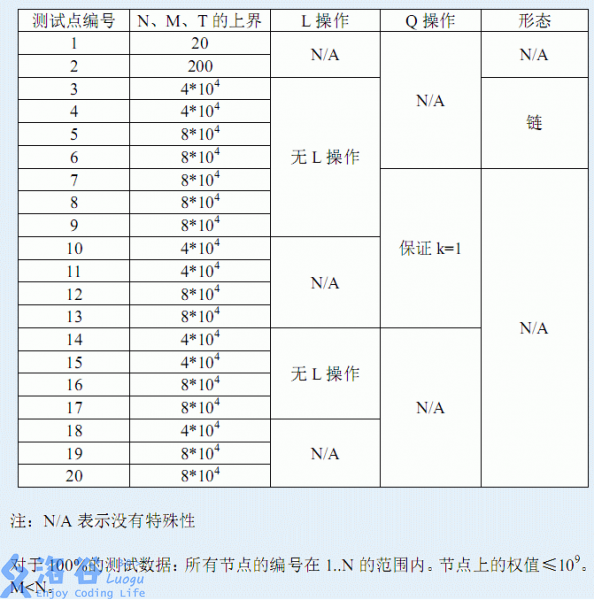
对于所有的数据，n,m,T<= 8*10^48∗104 .

输入输出格式

输入格式：

第一行包含一个正整数testcase，表示当前测试数据的测试点编号。保证1<=testcase<=20。

第二行包含三个整数N，M，T，分别表示节点数、初始边数、操作数。

第三行包含N个非负整数表示 N个节点上的权值。

接下来 M行，每行包含两个整数x和 y，表示初始的时候，点x和点y 之间有一条无向边。

接下来 T行，每行描述一个操作，格式为”Q x y k“或者”L x y “，其含义见题目描述部分。

输出格式：

对于每一个第一类操作，输出一个非负整数表示答案。

输入输出样例

输入样例#1： 复制

1
8  4 8
1  1 2 2 3 3 4 4
4  7
1  8
2  4
2  1
Q 8 7 3 Q 3 5 1
Q 10 0 0
L 5 4
L 3 2 L 0 7
Q 9 2 5 Q 6 1 6

输出样例#1： 复制

2
2
1
4
2

说明

对于第一个操作 Q 8 7 3，此时 lastans=0，所以真实操作为Q 8^0 7^0 3^0，也即Q 8 7 3。点8到点7的路径上一共有5个点，其权值为4 1 1 2 4。
这些权值中，第三小的为 2，输出 2，lastans变为2。

对于第二个操作 Q 3 5 1 ，此时lastans=2，所以真实操作为Q 3^2 5^2 1^2 ，也即Q 1 7 3。点1到点7的路径上一共有4个点，其权值为 1 1 2 4 。
这些权值中，第三小的为2，输出2，lastans变为 2。之后的操作类似。

代码

显然树上第k大直接主席树

如果连边的话，我们重构小的那一棵，连到另一棵上。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 80011
#define M 10000000
 
using namespace std;
 
int n, m, T, cnt, tot, test, last;
int head[N], to[N << 2], nex[N << 2], val[N], ntr[N], deep[N], f[N][21], root[N], sum[M], ls[M], rs[M], fa[N], size[N];
bool vis[N];
 
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + ch - '0';
    return x * f;
}
 
inline void add(int x, int y)
{
    to[cnt] = y;
    nex[cnt] = head[x];
    head[x] = cnt++;
}
 
inline int find(int x)
{
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}
 
inline void Union(int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx != fy) fa[fx] = fy, size[fy] += size[fx];
}
 
inline int query(int a, int b, int c, int d, int l, int r, int x)
{
    if(l == r) return l;
    int mid = (l + r) >> 1;
    if(sum[ls[a]] + sum[ls[b]] - sum[ls[c]] - sum[ls[d]] >= x) return query(ls[a], ls[b], ls[c], ls[d], l, mid, x);
    else return query(rs[a], rs[b], rs[c], rs[d], mid + 1, r, x - (sum[ls[a]] + sum[ls[b]] - sum[ls[c]] - sum[ls[d]]));
}
 
inline void insert(int &now, int last, int l, int r, int x)
{
    now = ++tot;
    ls[now] = ls[last];
    rs[now] = rs[last];
    sum[now] = sum[last] + 1;
    if(l == r) return;
    int mid = (l + r) >> 1;
    if(x <= mid) insert(ls[now], ls[last], l, mid, x);
    else insert(rs[now], rs[last], mid + 1, r, x);
}
 
inline void dfs(int u)
{
    int i, v;
    vis[u] = 1;
    deep[u] = deep[f[u][0]] + 1;
    insert(root[u], root[f[u][0]], 1, m, val[u]);
    for(i = 0; f[u][i]; i++) f[u][i + 1] = f[f[u][i]][i];
    for(; i <= 20; i++) f[u][i] = 0;
    for(i = head[u]; ~i; i = nex[i])
    {
        v = to[i];
        if(!vis[v])
        {
            f[v][0] = u;
            dfs(v);
        }
    }
    vis[u] = 0;
}
 
inline int lca(int x, int y)
{
    int i;
    if(deep[x] < deep[y]) swap(x, y);
    for(i = 20; i >= 0; i--)
        if(deep[f[x][i]] >= deep[y]) x = f[x][i];
    if(x == y) return x;
    for(i = 20; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}
 
int main()
{
    char s[10];
    int i, x, y, k, fx, fy;
    test = read();
    n = read();
    m = read();
    T = read();
    memset(head, -1, sizeof(head));
    for(i = 1; i <= n; i++)
    {
        fa[i] = i, size[i] = 1;
        val[i] = ntr[i] = read();
    }
    for(i = 1; i <= m; i++)
    {
        x = read();
        y = read();
        add(x, y);
        add(y, x);
        Union(x, y);
    }
    sort(ntr + 1, ntr + n + 1);
    m = unique(ntr + 1, ntr + n + 1) - ntr - 1;
    for(i = 1; i <= n; i++) val[i] = lower_bound(ntr + 1, ntr + m + 1, val[i]) - ntr;
    for(i = 1; i <= n; i++)
        if(!deep[i]) dfs(i);
    while(T--)
    {
        scanf("%s", s);
        x = read() ^ last;
        y = read() ^ last;
        if(s[0] == 'Q')
        {
            k = read() ^ last;
            printf("%d\n", last = ntr[query(root[x], root[y], root[lca(x, y)], root[f[lca(x, y)][0]], 1, m, k)]);
        }
        else
        {
            fx = find(x), fy = find(y);
            if(size[fx] > size[fy]) swap(x, y);
            Union(x, y);
            f[x][0] = y;
            dfs(x);
            add(x, y);
            add(y, x);
        }
    }
    return 0;
}