【BZOJ1408】[Noi2002]Robot DP+数学

【BZOJ1408】[Noi2002]Robot

Description

Input

Output

Sample Input

3
2 1
3 2
5 1

Sample Output

8
6
75

HINT

90号机器人有10个老师，加上它自己共11个。其中政客只有15号；军人有3号和5号；学者有8个，它们的编号分别是：2,6,9,10,18,30,45,90。

题解：语文题，就是问你n的约数中μ(d)=0,1,-1时，φ(d)的和，其中令μ(1)=0,φ(2)=0

直接DP，令f[i][0/1]表示枚举到第i个素数，已选则不同奇素数为偶数/奇数个时的φ(d)的和，然后根据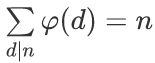，直接用n减去f[k][0]+f[k][1]就行了

#include <iostream>
#include <cstdio>
#include <cstring>
#define mod 10000
using namespace std;
const int maxn=10010;
int n,m;
int f[maxn][2],p[maxn],e[maxn];
int pm(int x,int y)
{
	int z=1;
	while(y)
	{
		if(y&1)	z=z*x%mod;
		x=x*x%mod,y>>=1;
	}
	return z;
}
int main()
{
	scanf("%d",&n);
	int i;
	for(m=i=1;i<=n;i++)	scanf("%d%d",&p[i],&e[i]),m=m*pm(p[i],e[i])%mod;
	f[0][0]=1;
	for(i=1;i<=n;i++)
	{
		if(p[i]==2)
		{
			f[i][0]=f[i-1][0];
			f[i][1]=f[i-1][1];
			continue;
		}
		f[i][0]=(f[i-1][0]+f[i-1][1]*(p[i]-1))%mod;
		f[i][1]=(f[i-1][1]+f[i-1][0]*(p[i]-1))%mod;
	}
	printf("%d\n%d\n%d\n",f[n][0]-1,f[n][1],(m-f[n][0]-f[n][1]+20000)%mod);
	return 0;
}