『Plotly实战指南』--直方图绘制与应用

在数据科学的世界里，直方图是一种不可或缺的可视化工具，它以其简洁而直观的方式，揭示了数据的内在规律，为数据分析和决策提供了有力支持。

它能够帮助我们快速识别异常值，并为统计推断提供有力支撑。

无论是对称的钟型分布，还是偏态的长尾分布，直方图都能清晰地呈现出来。

通过观察直方图的形状，我们可以了解数据的集中趋势和离散程度，从而为进一步的分析奠定基础。

本文从基础绘制到分析应用展开，介绍直方图的概念、代码实现以及实战场景。

1. 与柱状图区别

直方图是一种数据分布的图形化表示，通过矩形的高度反映数据的频数或频率。

它与柱状图有着本质区别：柱状图用于对比离散类别，而直方图则用于展示连续变量的分布。

直方图的核心作用在于观察分布的形状，例如对称性、偏态性、峰态以及长尾特征。

通过这些特征，我们可以识别数据的集中趋势和离散程度，为进一步的分析提供线索。

2. 绘制方式

在绘制直方图时，数据分组和区间设置至关重要。

Plotly 提供了自动分组功能，它会根据数据的规模和分布特征，自动选择合适的分组策略。

然而，在某些情况下，我们可能需要手动设置分组。通过Plotly的xbins参数，我们可以自定义区间边界或数量。

在选择分组策略时，我们需要平衡区间数量与数据特征的保留，如果区间过宽，可能会丢失重要信息；而如果区间过窄，又会导致直方图过于复杂，难以解读。

接下来，我们将通过代码实现一个简单的直方图。

首先，我们生成一个正态分布的数据集，然后绘制一个单变量直方图。

import plotly.express as px
import numpy as np

# 数据准备：生成正态分布数据
data = np.random.normal(loc=0, scale=1, size=1000)

# 绘制直方图
fig = px.histogram(
    data,
    x=data,
    histnorm="probability",
    title="正态分布直方图",
    labels={"x": "数值", "y": "概率"},
)

# 样式优化
fig.update_layout(
    xaxis_title="数值",
    yaxis_title="概率",
    bargap=0.2,  # 条形之间的间隔
    bargroupgap=0.1,  # 组内条形的间隔
)

fig.show()

绘制直方图的核心参数包括：

• x：指定数据列
• histnorm：频数统计模式，可以选择count（频数）、probability（概率）或density（密度）
• autobinx：是否启用自动分组。
• opacity：透明度调整，尤其在多数据集对比时，透明度可以增强可读性。

运行结果如下：

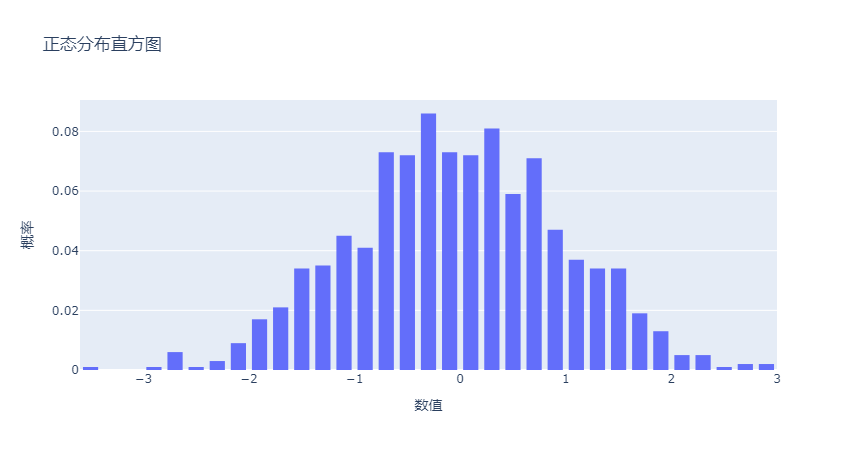
3. 分析应用

3.1. 分析数据分布特征

直方图不仅可以展示数据的分布形态，还可以帮助我们进行深入的分析。

通过对直方图的形态进行解读，我们可以判断数据的对称性、峰态以及长尾特征。

例如，钟型分布通常是对称的，而偏态分布则会呈现出明显的倾斜。

此外，直方图还可以帮助我们识别异常值，结合箱体图或 IQR 方法，我们可以标记出潜在的离群点。

在某些情况下，直方图的形状还可以辅助我们进行参数估计。比如，如果数据呈现出正态分布的形态，我们可以考虑使用正态分布模型进行拟合。

3.2. 不同数据集对比

在实际应用中，我们常常需要对比多个数据集的分布特征。

例如，我们可以使用多痕迹直方图（overlay 模式）进行叠加显示对比，或者使用分组直方图（group 参数）将不同数据集并排排列。

以下是一个实战案例，展示如何在 A/B 测试中对比用户行为分布：

import plotly.graph_objects as go

# 数据准备：假设 A 组和 B 组的点击量数据
data_A = np.random.normal(loc=5, scale=2, size=1000)
data_B = np.random.normal(loc=7, scale=2.5, size=1000)

# 绘制多痕迹直方图
fig = go.Figure(
    data=[
        go.Histogram(x=data_A, histnorm="probability", name="A 组"),
        go.Histogram(x=data_B, histnorm="probability", name="B 组"),
    ]
)

# 设置布局
fig.update_layout(
    title="A/B 测试用户点击量分布对比",
    xaxis_title="点击量",
    yaxis_title="概率",
    bargap=0.2,
    bargroupgap=0.1,
    barmode="overlay",  # 设置为叠加模式
)

fig.show()

叠加模式的显示效果如下：

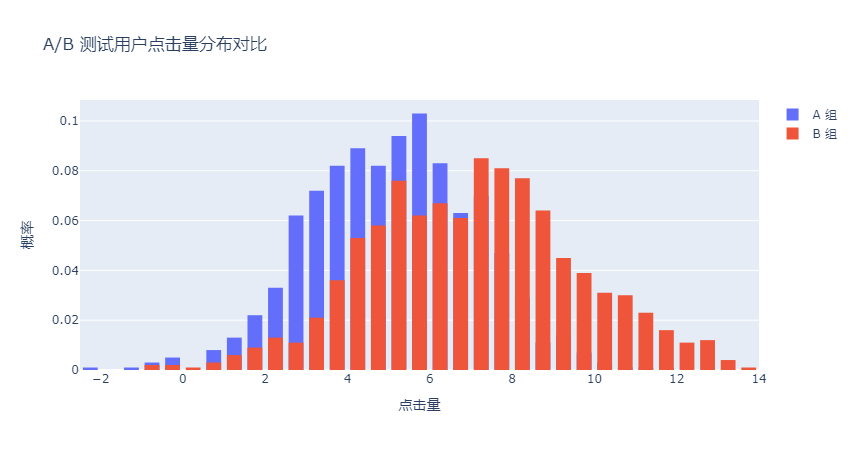
将代码中的barmode="overlay"改为barmode="group"，就会以分组模式显示。

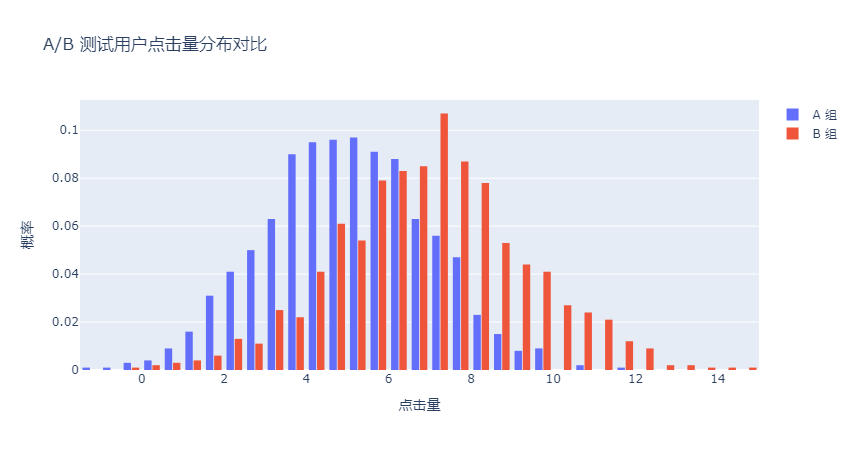
4. 总结

总得来说，直方图在探索性数据分析（EDA）中具有不可替代的作用，它能够快速建立数据直觉，帮助我们发现数据的分布特征和潜在问题。

在实践中，我们建议根据数据规模动态调整分组策略，避免信息丢失或过度拟合。

同时，结合箱线图、核密度估计图（KDE）进行多维验证，可以进一步提升分析的准确性。

在业务报告中，直方图能够直观地传递数据分布规律与组间差异，为决策提供有力支持。