二叉排序树BST及CRUD操作

摘要

构造一颗二叉排序树(也叫二叉搜索树，BST，Binary Search Tree)十分简单。一般来讲，大于根节点的放在根节点的右子树上，小于根节点的放在根节点的左子树上(如果等于根节点，则可视情况而定)，如果写程序的话，可以采用递归的方式，而且由于不存在重叠子问题的情况，因此递归的性能已经足够好(不考虑栈溢出的情况)。

二叉排序树在通常情况下可以达到O(lgN)的静态、动态操作的时间复杂度，但是存在一种特殊情况，即输入的数据本身就是有序的，这时二叉排序树退化成向量。

下面我们系统归纳一下二叉树的特性，以及相关操作及其代码实现。

二叉排序树

简称BST，也称为二叉查找树。其或是一棵空树，或是一棵具有下列特性的非空二叉树：

1）若左子树非空，则左子树上所有结点关键字值均小于根结点的关键字值。

2）若右子树非空，则右子树上所有结点关键字值均大于根结点的关键字值。

3）左、右子树本身也分别是一棵二叉排序树。

其是一个递归的数据结构。

左子树结点值 < 根结点值 < 右子树结点值

对其进行中序遍历可以得到一个递增的有序序列。

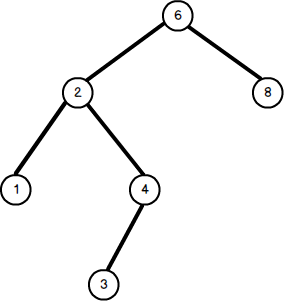
图1. 二叉排序树示例图

CRUD操作

Create-构造二叉排序树

构造一棵二叉排序树就是依次输入数据元素，并将它们插入到二叉树中的适当位置上的过程。

具体过程：

1）每读入一个元素，就建立一个新节点。

2）若二叉排序树非空，则将新结点的值与根结点的值比较。如果小于根结点的值，则插入到左子树中，否则插入到右子树中。

3）若二叉排序树为空，则新结点作为二叉树的根结点。

void Create_BST(BiTree &T, KeyType str[], int n) {
  //用关键字数组str[]建立一个二叉排序树
  T = NULL; //初始时bt为空树
  int i = 0;
  while(i < n) {  //依次将每个元素插入
    BST_Insert(T, str[i]);
    i++;
  }
}

Retrieve-查找二叉排序树的某结点

二叉排序树的查找是从根结点开始，沿某一分支逐层向下进行比较的一个递归的过程。

具体查找过程是：

1）若二叉树非空，将给定值与根结点的关键字比较，若相等，则查找成功；

2）若不等，则当根结点的关键字大于给定关键字值k时，在根结点的左子树中查找；

3）当根结点的关键字小于给定关键字值k时，在根结点的右子树中查找。

二叉排序树的非递归查找算法：

BSTNode *BST_Search(BiTree T,ElemTypr key,BSTNode *&p) {
  //查找函数返回值指向关键字值为key的结点指针，若不存在，返回NULL
  p = NULL; //p指向被查找结点的双亲，用于插入和删除操作中
  while(T != NULL && key != T->data) {
    p = T;
    if(key < T->data) {
      T = T->lchild;
    } else {
      T = T->rchild;
    }
    return T;
  }
}

Update-插入结点到二叉排序树中

二叉排序树作为一种动态集合，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时再进行插入。

由于二叉排序树是递归定义的，其插入结点的过程是：

1）若原二叉树为空，则直接插入结点；

2）否则，若关键字k小于根结点关键字，则插入到左子树中；

3）若关键字k大于根结点关键字，则插入到右子树中。

int BST_Insert(BiTree &T, KeyType k) {
  //在二叉=排序树T中插入一个关键字为k的结点
  if(T == NULL) {
    T = (BiTree)malloc(sizeof(BSTNode));
    T->key = k;
    T->lchild = T->rchild = NULL;
    return 1;  //返回1，表示成功
  } else if(k == T-> key) {  //树中存在相同关键字的结点
    return 0;
  } else if(k < T->key) {  //插入到T的左子树中
    return BST_Insert(T->lchild, k);
  } else {
    return BST_Insert(T->rchild, k);
  }
}

由此可见，插入的新结点一定是某个叶结点。下图是向二叉树插入结点28的过程，其中虚线表示查找路径。

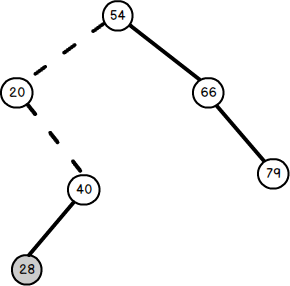
图2. 向二叉排序树插入结点28

Delete-删除二叉树的结点

在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须把被删除结点从存储二叉排序树的链表上摘下，将因删除结点而断开的二叉链表重新链接起来，同时确保二叉排序树的性质不会丢失。

删除操作的实现过程按3种情况来处理：

1）如果被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。

2）若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。

3）若结点z有左、右两棵子树，则令z的直接后继【中序第一个子女】（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继【中序第一个子女】（或直接前驱），这样就转换成了第一或第二种情况。

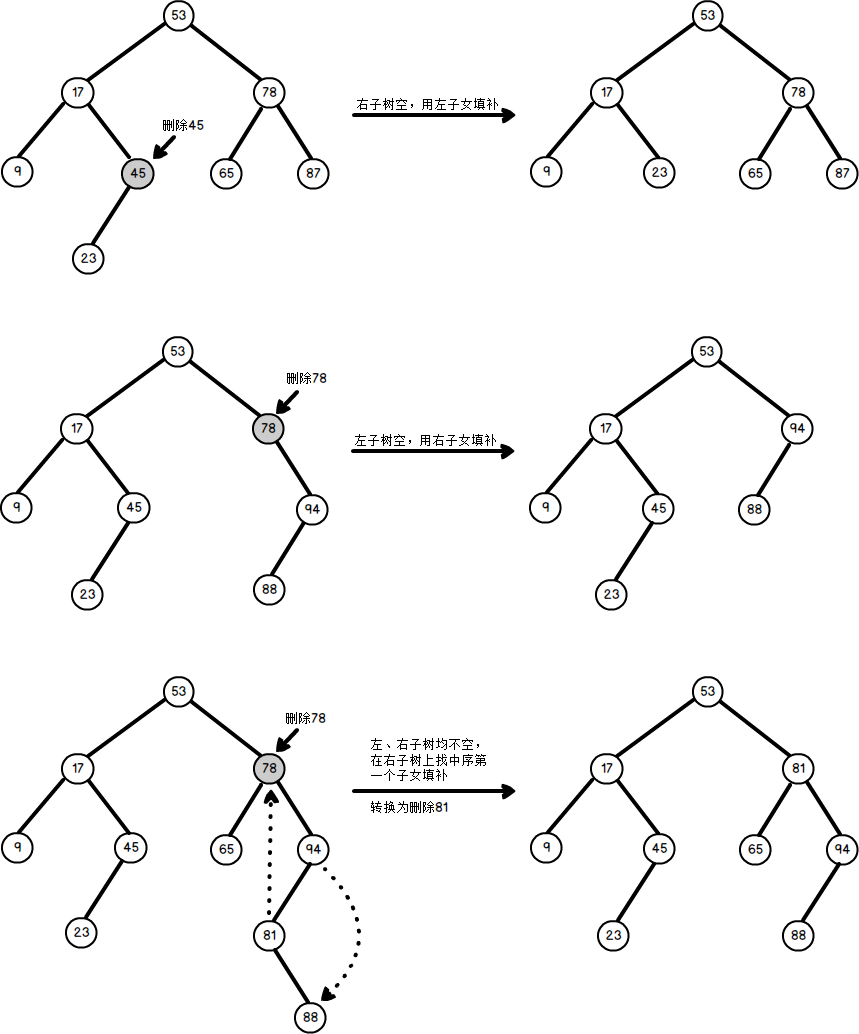
图3. 3种情况下的删除过程

参考

[1] miao_zheng. 二叉排序树、平衡二叉树、B树&B+树、红黑树的设计动机、缺陷与应用场景[OL]. cnblogs, 2018-02-28/2020-06-20

[2] 王道论坛. 2019年数据结构考研复习指导[M].北京:电子工业出版社, 2018:153-155.