P2216 理想的正方形题解

P2216 理想的正方形

（为什么要写这篇题解？因为我β搞的心态炸了）

食用此题解所需：有基础的双端队列知识与一只可爱的 $C++$

1. 思考

嗯，一看数据范围，$a,b \leq 1,000$ ，就知道这道题一定是一道 $\operatorname{O}(ab)$ 的题（因为输入就已经达到 $100,000$ 级别了，就算是 $\operatorname{O}(abn)$ 也过不去，顶多加一两个常数）

所以，$\operatorname{O}(abn^2)$ 的暴力是过不去哒！

既然暴力过不去，那么 $\dots$ 就换一个角度！

先单独考虑一个 $n \cdot n$ 的正方形，我们可以把它切片，切成每一份为 $1 \cdot n$ 的长方形，得出每一片长方形的最小值、最大值，然后再合并，也就是取最小、最大。

（图不严谨，只是稍微解释一下冲向的描述）

然后考虑横向的一排正方形，观察每个正方形最上面的一块切片，发现 $\dots$ 没错，这就是一个 区间移动求最值 的过程，而区间的长度恰恰为 $n$ 。

我们可以将最大值与最小值存下来，那么 $dpmin_{i,j}$ 就表示第 $i$ 行 $j-n+1$ ~ $j$ 这一条切片的最小值（最大值同理），显然，这玩意儿可以用双端队列优化。

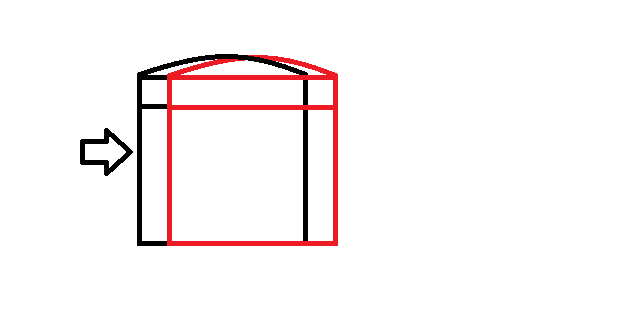
接下来，考虑纵向转移：将一个正方形最右边的一列割出来，由于这一列每一个坐标对应的 $dpmin$ 值都相当与一条长度为 $n$ 的切片，所以这一列上的 $n$ 个 $dpmin$ 值的最小值就是这个正方形的最小值。观察正方形纵向移动，这一列的变化 $\dots$ 也是 区间移动求最值 ！（当然啦，最大值也是同理）

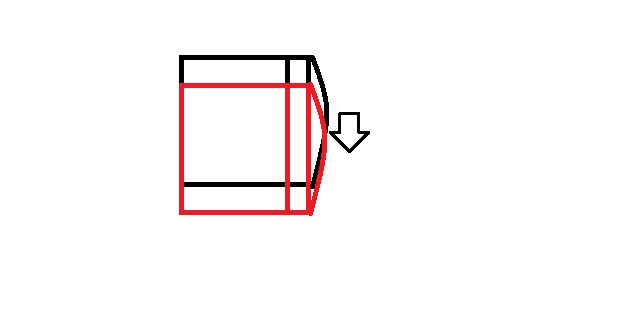
那么，在纵向求值后，每一个正方形的最大最小值就都求出来了。这道题，也就过了。

这样，我们只需一个 $dpmin$ 数组，一个 $dpmax$ 数组，一个存储输入数据的数组（可以优化成一维），和两个双端队列（重复使用，一个记最大值，一个记最小值），时间复杂度接近 $\operatorname{O}(ab)$ （双端队列操作也要时间，但是比较快的）

2. 警钟敲烂！

STL 使用前先判非空
两个双端队列代码差不多，但是千万别直接 Ctrl+C,Ctrl+V 然后改！容易混淆或漏掉！建议重新手写！

3. 代码

直接抄的话是会错的啦！是会 $AF$ 的啦！

#include<bits/stdc++.h>

using namespace std;

int a,b,n,vis[1005],dp1[1005][1005],dp2[1005][1005];

deque<int> quemin,quemax;

int main() {

    scanf("%d%d%d",&a,&b,&n);

    for(int i=1;i<=a;i++) {

        // 清空双端队列

        while(!quemin.empty()) quemin.pop_back();// 相比 pop_front 更快一些

        while(!quemax.empty()) quemax.pop_back();

        // 横向区间最值问题

        for(int j=1;j<=b;j++) {

            scanf("%d",&vis[j]);

            // 插入最小值队列

            while(!quemin.empty()&&quemin.front()<=j-n) quemin.pop_front();

            while(!quemin.empty()&&vis[quemin.back()]>=vis[j]) quemin.pop_back();

            quemin.push_back(j),dp1[i][j]=vis[quemin.front()];

            // 插入最大值队列

            while(!quemax.empty()&&quemax.front()<=j-n) quemax.pop_front();

            while(!quemax.empty()&&vis[quemax.back()]<=vis[j]) quemax.pop_back();

            quemax.push_back(j),dp2[i][j]=vis[quemax.front()];

        }

    }

    // 纵向更新双端队列，求出答案

    int ans=1e9;

    for(int j=1;j<=b;j++) {// 纵向

        // 基本同上

        while(!quemin.empty()) quemin.pop_back();

        while(!quemax.empty()) quemax.pop_back();

        for(int i=1;i<=a;i++) {

            while(!quemin.empty()&&quemin.front()<=i-n) quemin.pop_front();

            while(!quemin.empty()&&dp1[quemin.back()][j]>=dp1[i][j]) quemin.pop_back();

            quemin.push_back(i);

            while(!quemax.empty()&&quemax.front()<=i-n) quemax.pop_front();

            while(!quemax.empty()&&dp2[quemax.back()][j]<=dp2[i][j]) quemax.pop_back();

            quemax.push_back(i);

            if(i>=n&&j>=n) ans=min(ans,dp2[quemax.front()][j]-dp1[quemin.front()][j]);

        }

    }

    printf("%d\n",ans);

    return 1;// 抄代码有风险，做题请自己做，谢谢

}