解码C语言环境搭建之Linux子系统&使用vscode连接子系统

安装准备工作

1. 查看当前系统版本确保高于16215.0
   
   
2. 开启WSL
   
   Windows Subsystem for Linux（简称WSL）是一个为在Windows 10上能够原生运行Linux二进制可执行文件（ELF格式）的兼容层。
   
   
   
   

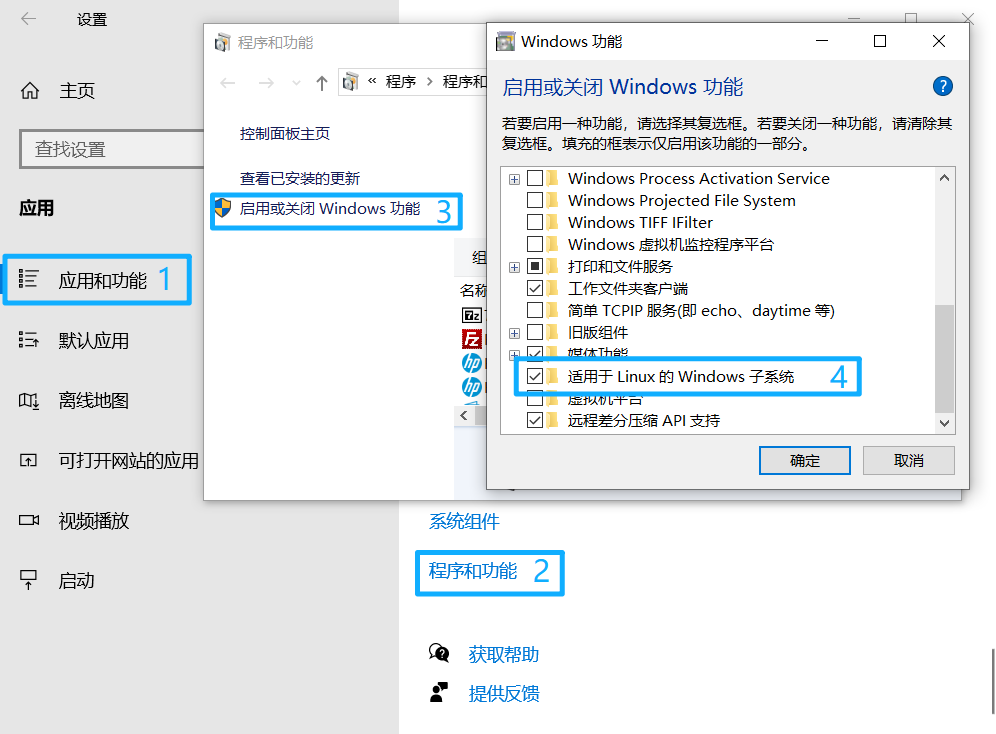
安装步骤

1. 微软商城Microsoft Store安装Ubuntu(本人安装的版本是22.04)
   
   
2. 点击
   
   
3. 等待安装完成输入用户名跟密码就可以使用了（注：密码不回显）
   
   

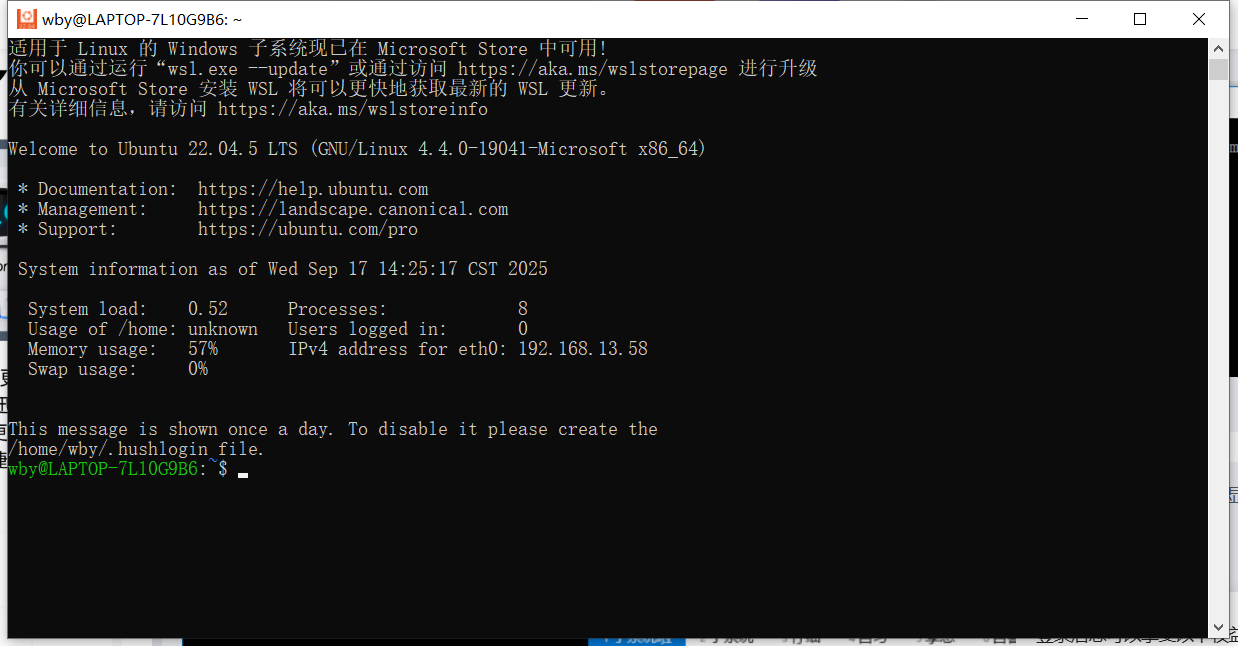
移动WSL到其他磁盘，释放C盘空间

1. 查看已安装的 Windows Subsystem for Linux (WSL) 发行版

wsl --list --verbose

1. 导出发行版到指定文件

wsl --export <发行版名称> <备份文件路径.tar>
eg:wsl --export Ubuntu-22.04 E:\wsl-backup\ubuntu-22.04.tar

1. 注销（卸载）原有发行版

wsl --unregister <发行版名称>
eg:wsl --unregister Ubuntu-22.04

1. 在新磁盘位置导入发行版

wsl --import <发行版名称> <目标安装目录> <备份文件路径.tar>
eg:wsl --import Ubuntu-22.04 E:\wsl\ubuntu E:\wsl-backup\ubuntu-22.04.tar

1. 恢复默认用户(导入后默认以 root 身份登录，需恢复原用户)

wsl -d <发行版名称>	//运行WSL
echo -e "[user]\ndefault=wby" >> /etc/wsl.conf	//在 WSL 内设置默认用户（假设原用户名为 `wby`）
exit	//退出并关闭 WSL
wsl --terminate <发行版名称>
wsl -d <发行版名称>	//再次启动即可生效

使用vscode连接Linux子系统

1. 安装WSL插件
   
   
   
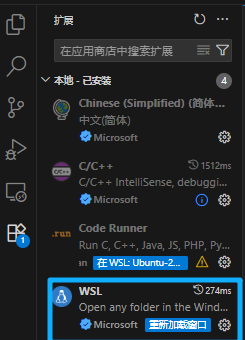
   2.选择终端默认配置文件
2. 使用vscode打开存储代码的文件夹,右键在终端打开即可
   
   

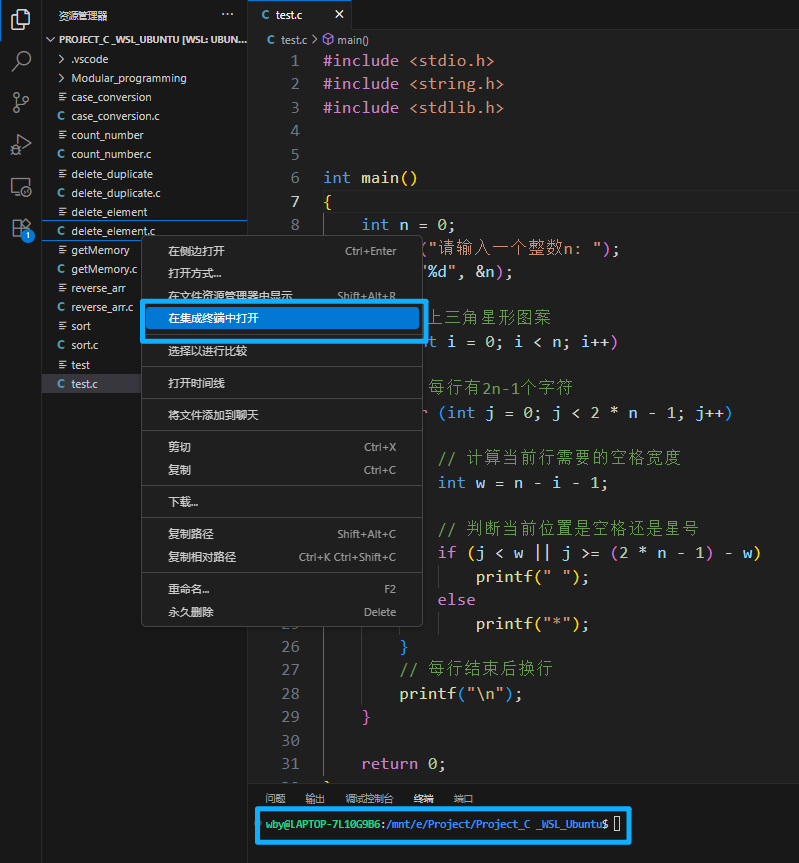
在安装gcc编译器前建议换源

1. 备份原始源文件
   
   在终端中运行以下命令，备份当前的 sources.list 文件：

sudo cp /etc/apt/sources.list /etc/apt/sources.list.backup

1. 编辑源文件
   
   使用文本编辑器打开 sources.list 文件：

sudo vim /etc/apt/sources.list

将文件中的内容替换为以下国内镜像源之一：

//阿里云镜像
deb https://mirrors.aliyun.com/ubuntu/ focal main restricted universe multiverse
deb https://mirrors.aliyun.com/ubuntu/ focal-security main restricted universe multiverse
deb https://mirrors.aliyun.com/ubuntu/ focal-updates main restricted universe multiverse
deb https://mirrors.aliyun.com/ubuntu/ focal-backports main restricted universe multiverse
//清华大学镜像
deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ focal main restricted universe multiverse
deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ focal-security main restricted universe multiverse
deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ focal-updates main restricted universe multiverse
deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ focal-backports main restricted universe multiverse

保存并退出（按 ESC，输入 :wq）。

3. 更新软件包列表

运行以下命令以更新软件包列表：

sudo apt update
sudo apt upgrade -y

安装gcc即可运行c语言代码

sudo apt install gcc