典型相关分析 CCA

最近有小伙伴在问我一个数据分析的问题, 做毕设, 实证分析. 不知道改如何处理数据.

看了下设计的量表大致是这样的, 都是 5级的里克特量表, 大致分为两波, X, Y. 小伙伴认为就只有两个变量, 这是从商业理论上来认识的, 但从数据的角度, 却不是的.

X: 一共有22个问题, 也就是22个字段; 里面又是有认为分组的, 三两个字段, 又被认定为一个别名.

Y: 一共有13个问题, 也就是13个字段; 里面有是人为分组, 三两字段啥的, 分为 4组, 分别有别名.

然后不知道该如何分析?

问题

探寻 X 与 Y 的相关关系(线性相关)

其实探讨的时候, 挺不易的, 就很难知道她到底想要分析什么, 需求是什么, 还以为要做什么回归分析, 什么相关分析, 什么统计描述或其他的, 总之, 沟通过程非常漫长. 最后我放弃了, 还是单纯从这个数据级来分析.

本质上, 其实宏观来看, 就是 X 和 Y 的相关性如何嘛, 以及如何影响的. 那这不是求一波, 相关系数嘛. 但这里, X, Y 是多个字段, 是多对多 的关系, 就求不来了. 因此需要引进新的方法.

CCA

于是引入了典型相关分析 (Canonical Correlation Analysis), 用于探索多变量之间的关联关系.

于是这个问题, 就可以初步这样来做.

更正一波,写的有点不对, 不是分别降低到一维度. 而是分别降维后, x 和 y 能进行 配对. 这里 y 有13个嘛, x 有22个, 假设根本不对 y 进行降维, 那最多也只能匹配到 13对. 约束条件就是相关系数最大呀. 这块的数学公式就暂时不写了, 跟 PCA , 因子分析的逻辑是类似的.

发现了一个神器, 在线SPSS, 叫做 SPSSAU, 付费的, 但功能强大, UI 很有感觉, 重点是完全实现 傻瓜式操作. 虽然我已经不再做这块了, 但还是很怀念 SPSS, 比较是我数据分析之路的启蒙软件. 至少是真正用来做数据分析, 做市场研究的.

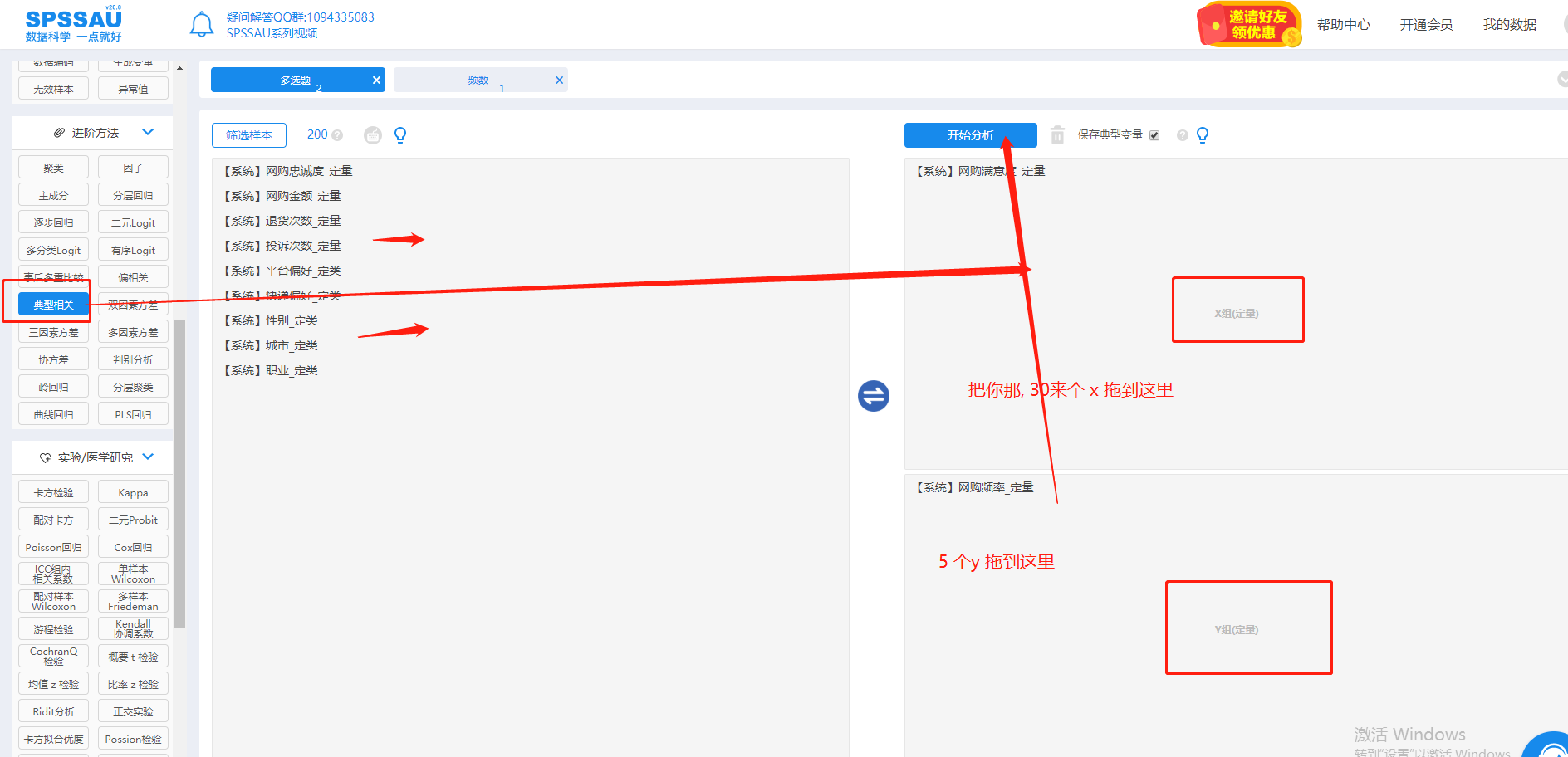
简单, 托拉拽, 一键输出报告, 包含 假设检验. 探寻数据的应用意义, 而不用太多关注底层的数学公式. 虽然数学公式会更加帮助理解数据集, 这是后话. 我觉得这才是数据分析的意义:

• 描述性统计分析
• 关联性统计分析
• 探索性建模分析

这种基于统计理论的分析框架 + 商业理论, 已早已熟练于心. 虽然现在的不用这类 傻瓜工具了, 现在自己搞编程, 但我感觉企业中的数据分析, 至少我接触的反而更加低级.

• 写 sql 查询数据 或 手动下载数据
• 筛选字段, 合并表格
• 计算业务指标, 几遍的加减乘除, 什么同比环比
• 大量的分组聚合, 生成报表, 看板

真的是, 从技术层面, 毫无难度. 我很多时间都是干这些活, 相比数据分析,我认为的, 我感觉还真不如几年前用 SPSS 的时光. 起码是真的再利用数据的价值来进行市场研究, 市场分析.

然后会最终得到这样类似的结果 , 和一些假设检验, 因子载荷等的术语, 都蛮简单的. (我没跑, 数据暂不能公开, 找了一张网上的示意图)

这样 CCP 就完成了, 多自变量 和 多因变量的关联分析了.

Next - 回归

继续要探寻, X 和部分 y 的关系. 我的思路, 都既然做相关分析了, 那很自然再拓展到回归分析呀.

合并 y 为 1 列

回归分析的 y 是一个字段, 因此, 可以将 量表中的 小 y 组进行, 合并为一列. 这里, 可以加权 或者 直接平均, 自己能解释清楚就行.

主成分 + 多元回归

有一个 y, 有很多的 x1, x2, x2... 相关分析, 就是要判断, 这些 x1, x2..与 y 是都是分别有线性相关性的(相关系数高); 而 x1, 与 x2, x3.. 之间呢, 彼此相关系数 要低

第二步就是要降维. 为啥必须要降维度呢, 就是怕 X 矩阵, 存在共线, 然后就不能 求 逆了呀.

PCA降维

至于如何降维, 我感觉我自己都说烂了. 也搞好几年了, 就是让特征重新进行线性组合 (改变数据了哦) 为几个较少得到特征, 然后尽可能保留原来更多的信息 (协方差的范数尽可能大)

求解模型参数

方法1 是一步求解, 就用上面的共线图中的矩阵运算即可.

方法2 是用梯度下降法来做, 我用的多, 但这个小伙伴, 没有学过编程, 就还是给推荐, 撒花是点点点算了.

小结

• 多自变量 和 多因变量 分析可以考虑 典型相关分析 CCA 这种 "降维配对" 的技术
• 回归分析必须 3步: 先做相关性分析; 再做降维处理; 再训练模型参数;
• PCA 我感觉非常厉害的. 还有一在线版spssau 的工具体验感很好, 市场研究方面的数据处理, 很适合.