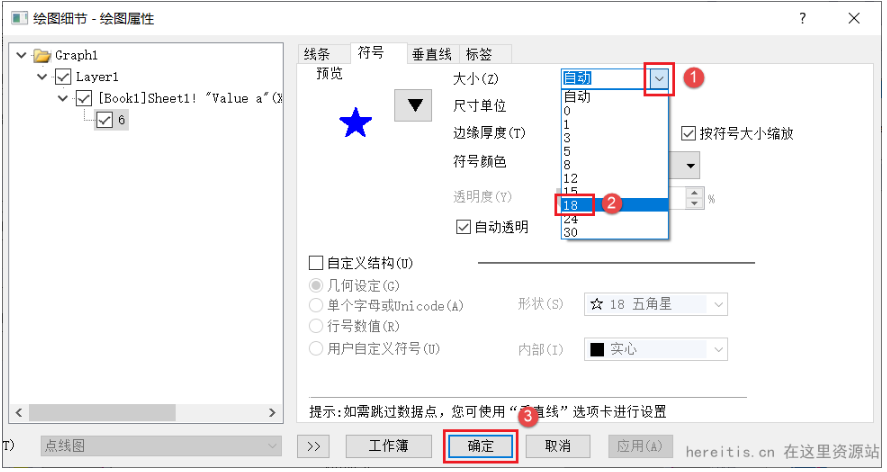
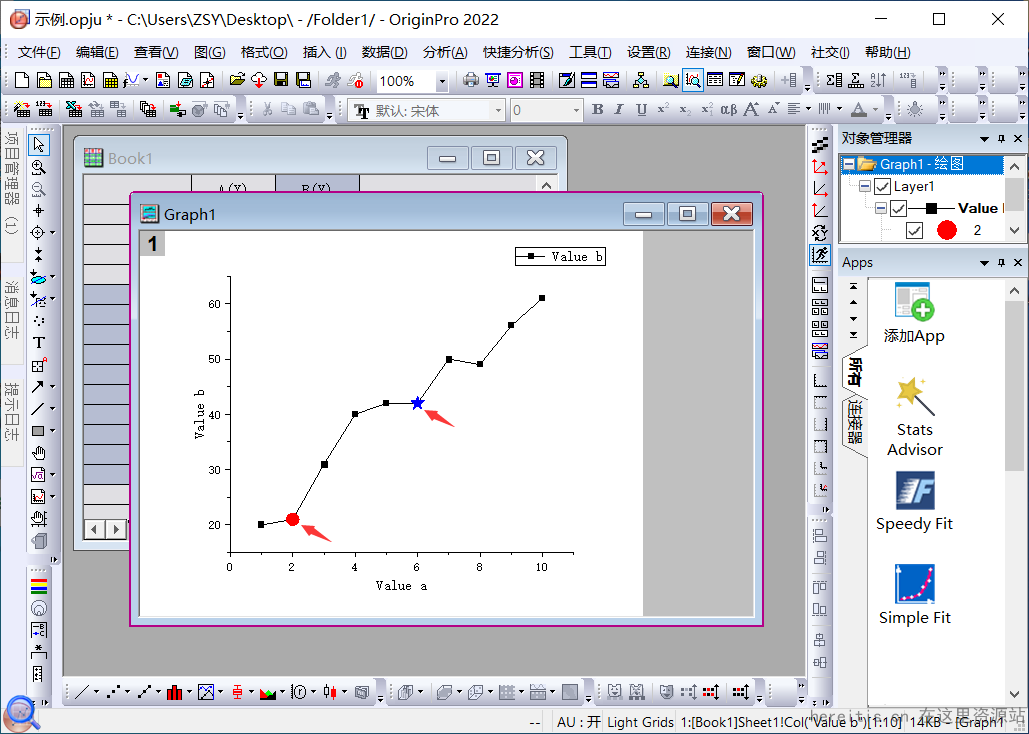
Origin如何对图中的某一点进行个性化设置?
Origin软件是一款由美国OriginLab公司开发的科学数据分析和可视化软件,其主要功能包括数据导入、数据处理、数据可视化、统计分析、信号处理等。它可以帮助科学家、工程师、研究人员等更加方便地处理和分析实验数据。
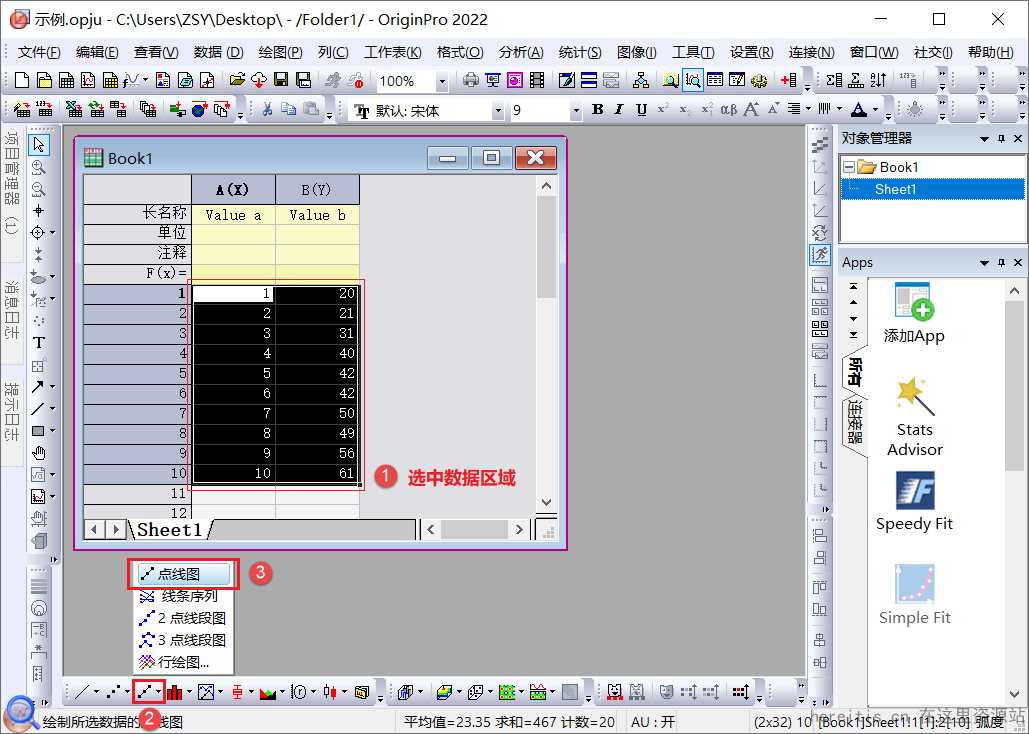
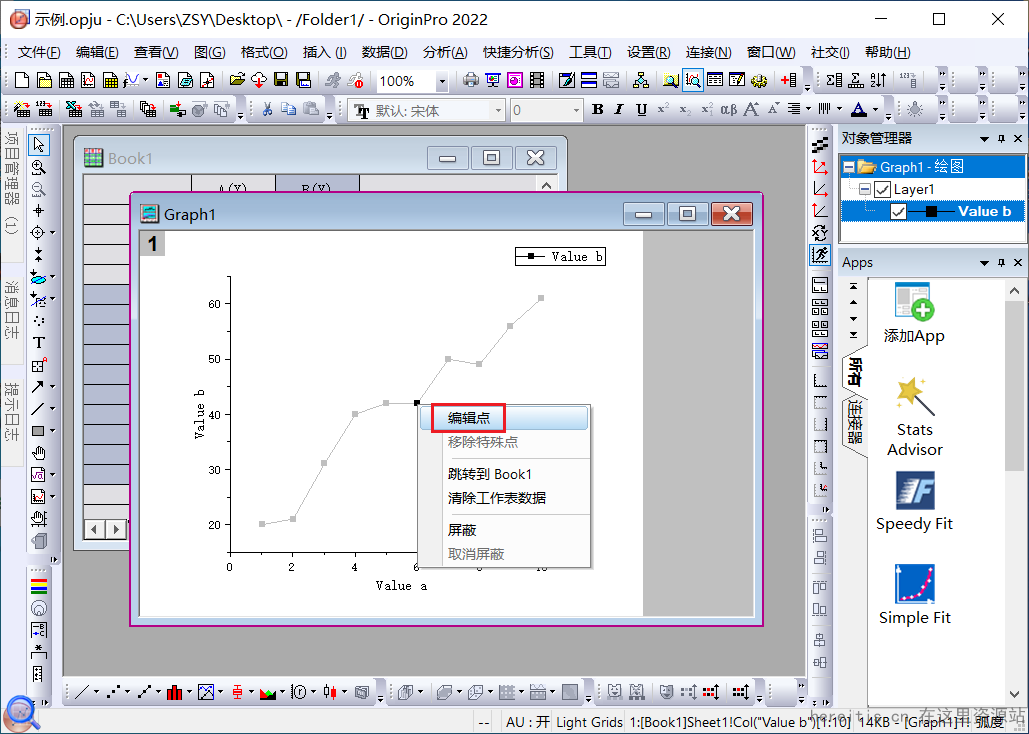
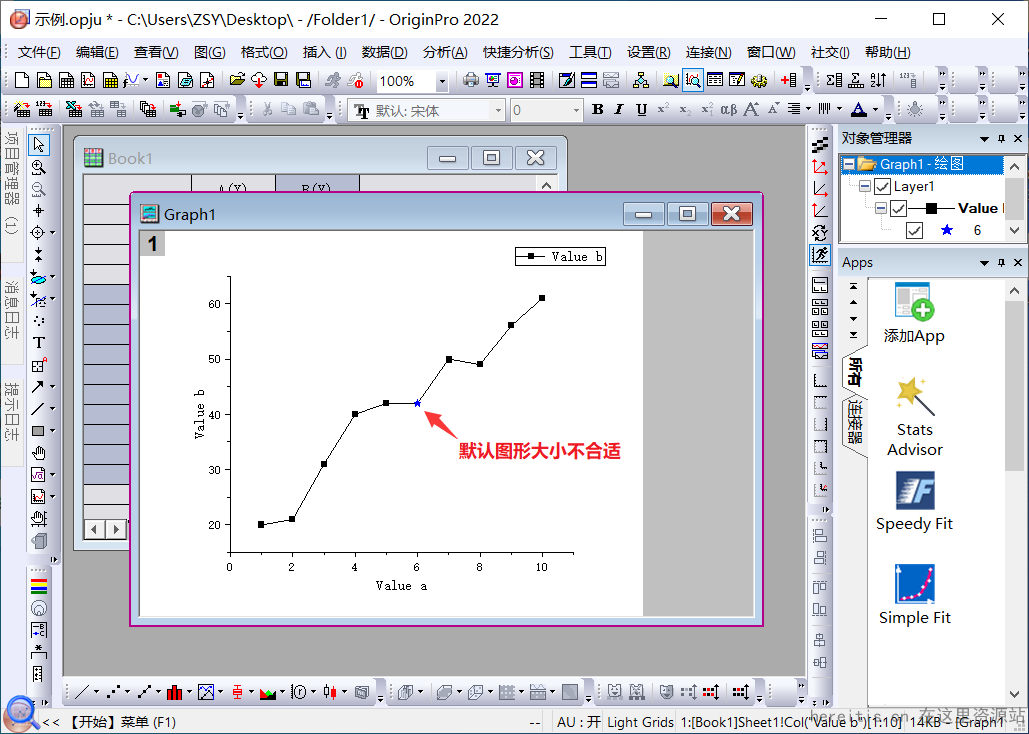
我们使用Origin把离散的数据绘制成一个带点的折线图,如下,如果我们想调整,只能对整条曲线上的点进行调整;
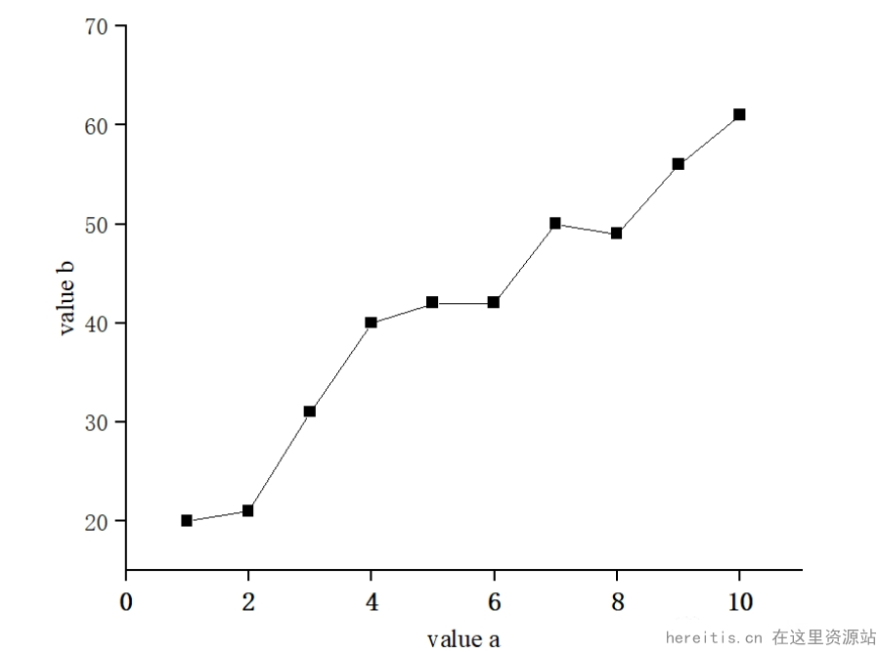
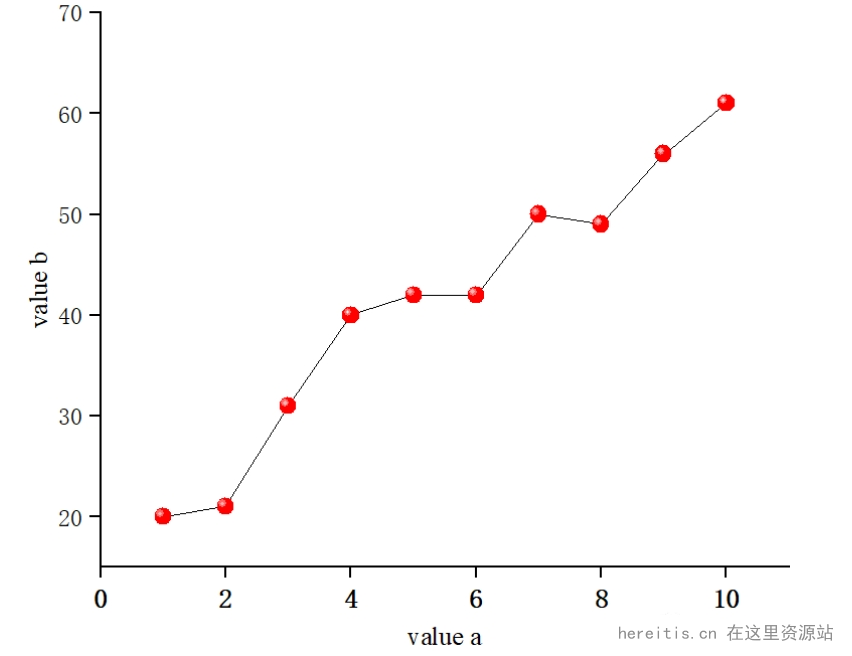
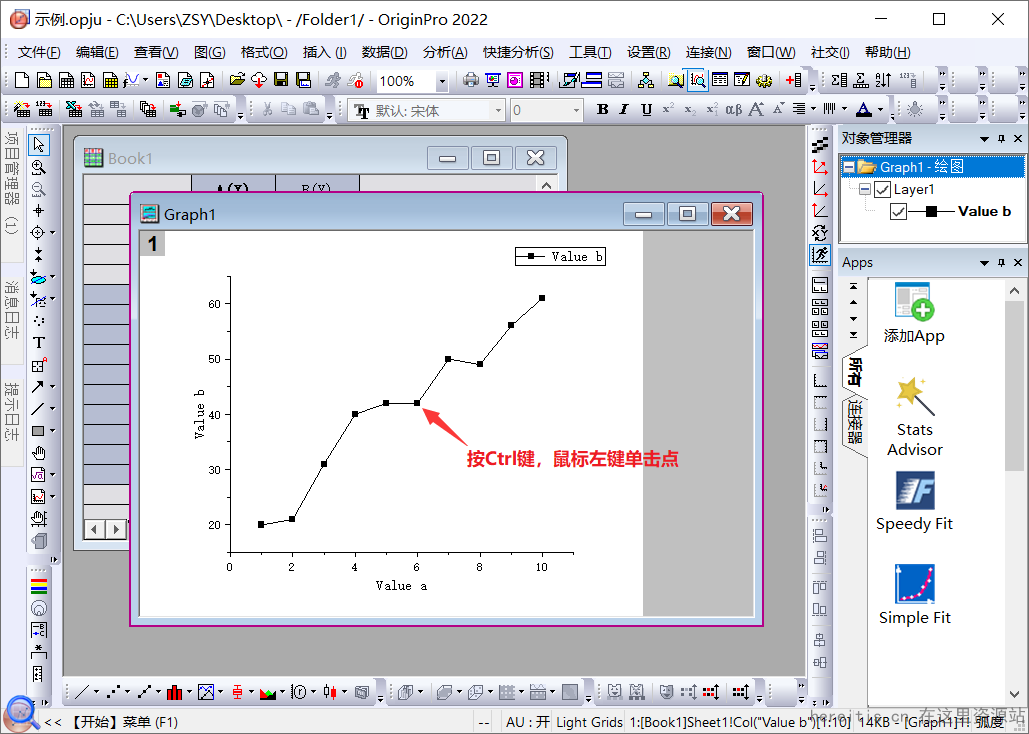
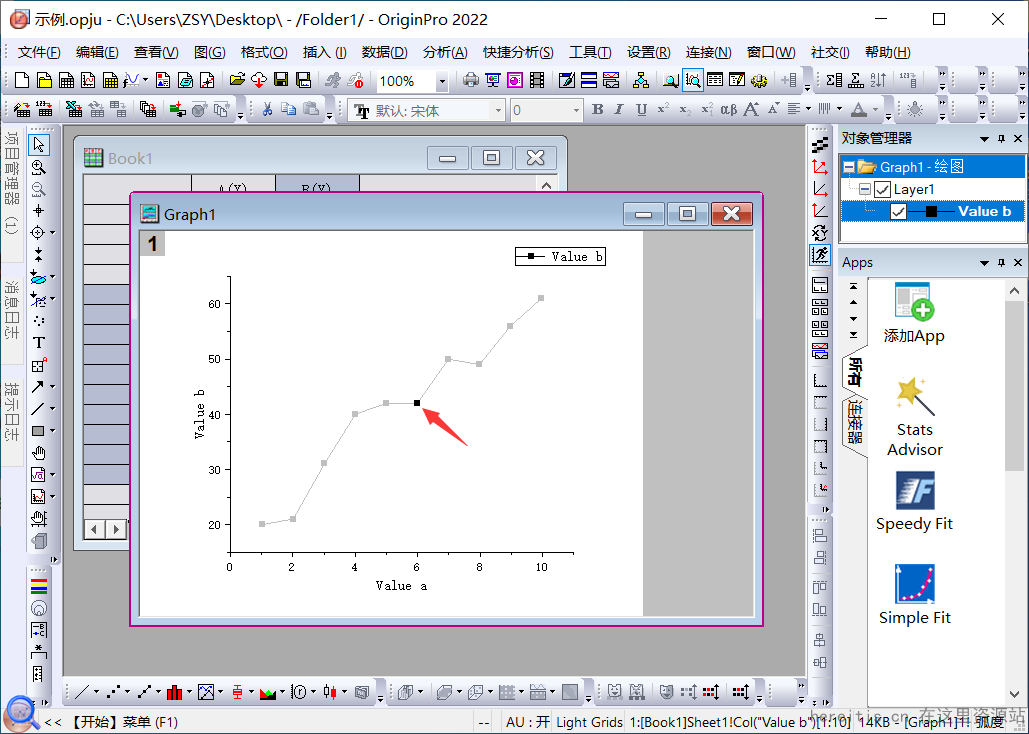
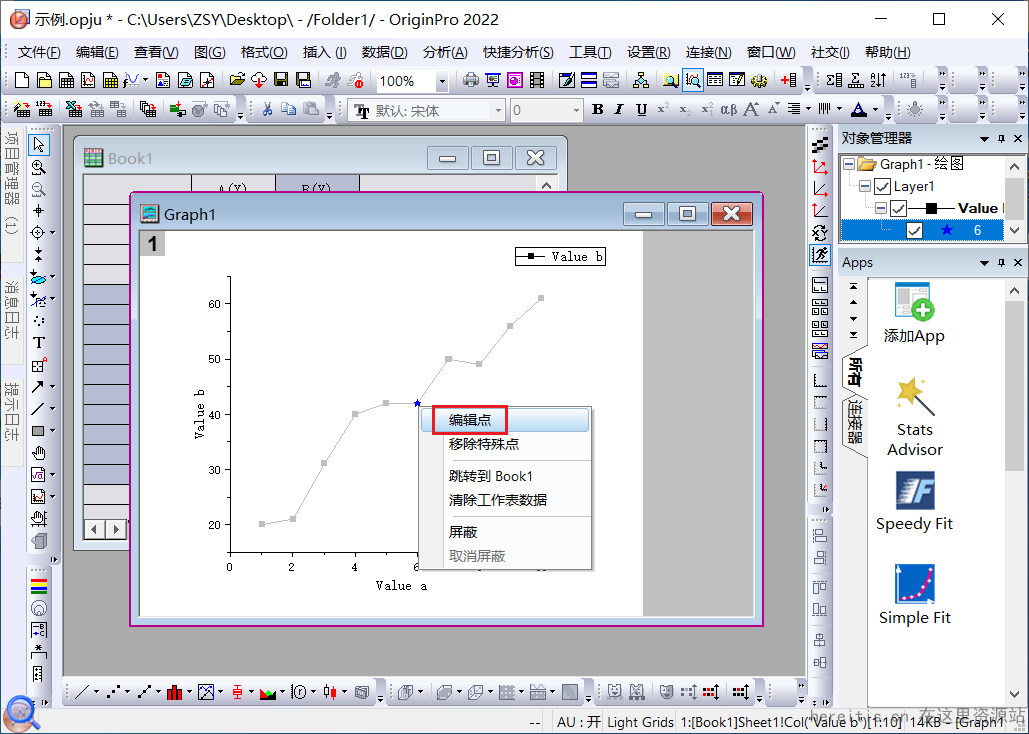
但很多场景我们需要的是突出某一点,只想对其中的一两个点做特殊化处理,应该怎么办呢?
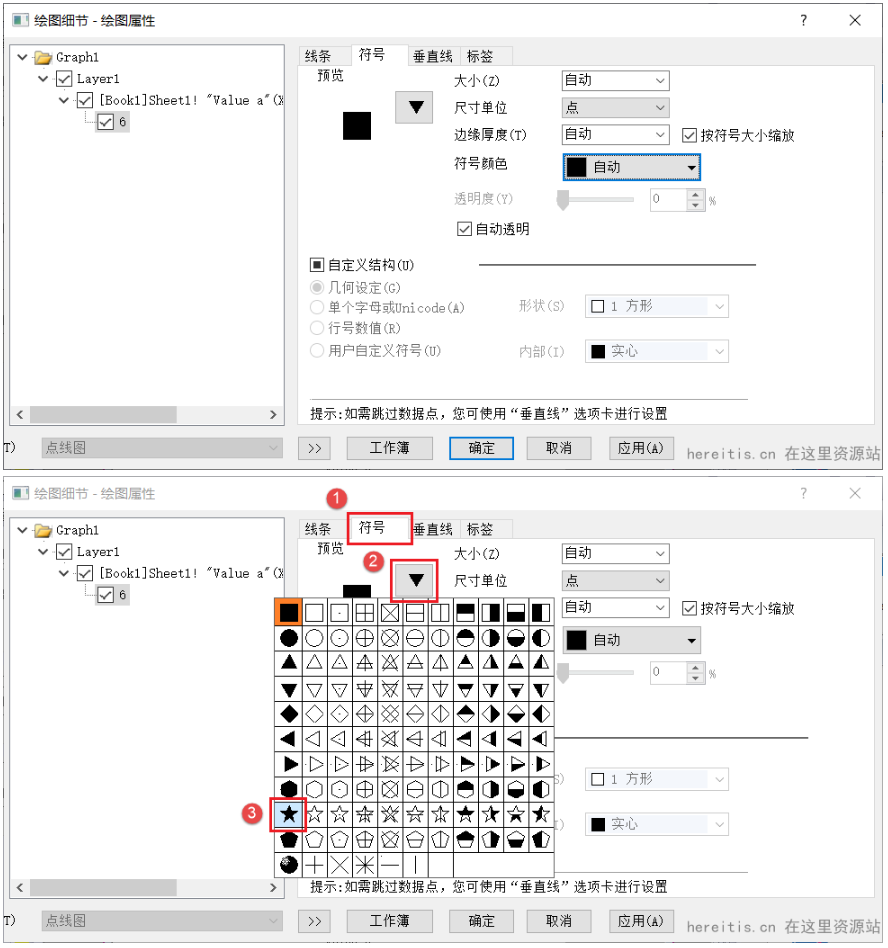
操作步骤:
1、打开Origin2022软件,输入如下数据:
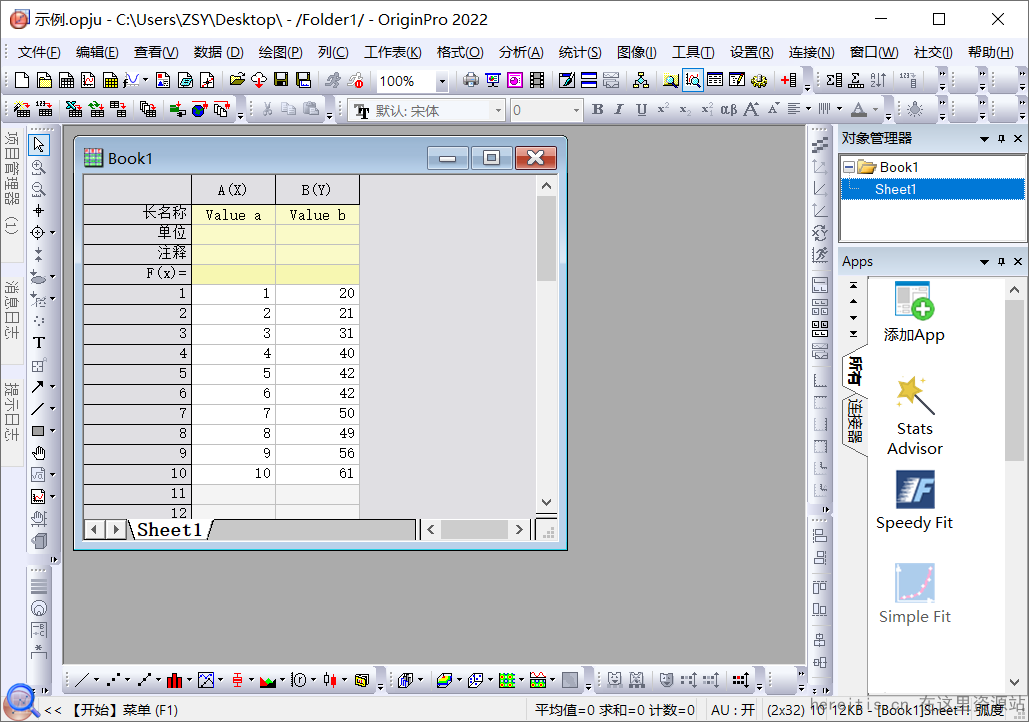
Origin如何对图中的某一点进行个性化设置?的更多相关文章
- Ubuntu 14 中,SecureCRT、SecureFX个性化设置
[SecureCRT 个性化设置] 打开设置路径:菜单栏 -> Opions -> Global Options -> General -> Default Session - ...
- 在图中寻找最短路径-----深度优先算法C++实现
求从图中的任意一点(起点)到另一点(终点)的最短路径,最短距离: 图中有数字的点表示为图中的不同海拔的高地,不能通过:没有数字的点表示海拔为0,为平地可以通过: 这个是典型的求图中两点的最短路径:本例 ...
- echarts的pie图中,各区块颜色的调整
今天在学习使用echarts生成各种图表. 然后在使用pie图时出现我无论怎么更改代码中的颜色,pie图中各块的颜色都十分相近,几乎没法区别块与块之间的区别,如下图: 在下图中,除了其中一块的是红色的 ...
- 【uml】之类图中的关系 标签: uml图形类 2014-11-29 09:02 1198人阅读 评论(23)
uml早就画完了图,但是自己迟迟没有总结,因为总觉的自己把握的不到位,虽然现在也还是不到位,废话少说,上篇博客总结了用例图中的几种关系,这篇就讨论一下类图中的几种关系. 在uml的所有图中,就我目前的 ...
- UML图中经常用到几种的关系图例
学习这个东西挺奇怪的,时间一长就容易忘记,或者记不清楚.今天看到一些UML图的关系,发现有些出入了,索性就写下来,以后再忘记的时候过来看看. 在UML的类图中,常见的有以下几种关系: 继承(Gener ...
- 使用axes函数在matlab绘图中实现图中图的绘制
使用axes函数在matlab绘图中实现图中图的绘制 有时为了对细节进行详细说明,需要在一个较大坐标轴上绘制一个小图来对局部进行放大以阐述结果. 这可以通过调用axes函数实现. 下面通过绘制 y=1 ...
- opencv删除二值图中较小的噪点色块
CvSeq* contour = NULL; double minarea = 100.0; double tmparea = 0.0; CFileDialog dlg(true); if (dlg. ...
- javascript实现有向无环图中任意两点最短路径的dijistra算法
有向无环图 一个无环的有向图称做有向无环图(directed acycline praph).简称DAG 图.DAG 图是一类较有向树更一般的特殊有向图, dijistra算法 摘自 http://w ...
- 分布式监控系统Zabbix-3.0.3-完整安装记录(4)-解决zabbix监控图中出现中文乱码问题
之前部署了Zabbix-3.0.3监控系统,在安装数据库时已经将zabbix库设置了utf-8字符. 首先确定zabbix开启了中文支持功能:登录到zabbix服务器的数据目录下(前面部署的zabbi ...
- 图中最短路径算法(Dijkstra算法)(转)
1.Dijkstra 1) 适用条件&范围: a) 单源最短路径(从源点s到其它所有顶点v); b) 有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E ...
随机推荐
- 赣CTF-Misc方向wp
checkin 下载附件,一张图片,拖进010,在文件尾看到隐藏文本,提取并用社会主义价值解密 ez_forensics 提示为结合题目进行想象,我们会想到取证第一步vc挂载,但是需要密码,研究图片, ...
- WPF 窗口 触摸失效 的一种场景
最近,生产线反馈,在执行生产大屏测试软件的时候,软件大概率出现不能触摸,但是可以用鼠标的的情况.刚好 这个软件又是WPF 做的,所以做了以下排查. .Net 环境: .NetFrameWork 4.8 ...
- Odoo14前端框架常用操作
单页Web应用(single page web application,SPA): SPA 是一种特殊的 Web 应用,是加载单个 HTML 页面并在用户与应用程序交互时动态更新该页面的. 它将所有的 ...
- Spring AOP 面向切面编程之AOP是什么
前言 软件工程有一个基本原则叫做"关注点分离"(Concern Separation),通俗的理解就是不同的问题交给不同的部分去解决,每部分专注于解决自己的问题.这年头互联网也 ...
- Re:prime 关于质数的算法
Re:prime 关于质数的所有算法 绪言 所有代码若无说明,均采用快读模板 关于质数,无非就两大类: 判断一个数字是不是质数 找出[1,n]中所有的质数 先讲1: Judge 判断x是不是质数 根据 ...
- ArkUI-X中Plugin生命周期开发指南
ArkUI-X插件用于拓展ArkUI应用的能力,提供管理插件生命周期的能力.本文主要介绍Android平台的ArkUI-X插件生命周期的使用. Android平台创建ArkUI-X插件生命周期 在An ...
- 全球首个无限执行的 AI 出现!给我玩爽了
给 AI 一句话,它就能自主执行任务,生成复杂的大型网站.几十页的 PPT.万字爆款图文.千万字长篇小说? 据说这是世界上第一款无限的 AI 智能体 -- Flowith. 无限这个词听起来有点东西啊 ...
- 2025年6月Docker镜像加速失效终极解决方案
以下是融合整理的Docker镜像加速终极解决方案,结合基础配置与深度技术方案,形成分层递进的完整体系: 一.分层加速架构 图表 二.全链路解决方案 1. 基础层:公共镜像源(5分钟快速配置) json ...
- Photoshop 2025超详细保姆级下载安装教程(直装版)
目录 一.Photoshop 2025软件简介 二.Photoshop 2025下载与安装教程(详细步骤) 三.Photoshop 2025核心功能亮点 四.Photoshop 2025常见问题与注意 ...
- [CF1580D]Subsequence
D - Subsequence 发现\(f(i,j)\)不好处理,考虑将其转换成另一个函数 考虑笛卡尔树,\(\min(a_i,a_{i+1},...,a_j)\)就是在笛卡尔树上,\(i\)和\(j ...