[游戏数据分析]WAU模型简介及WAU预测

声明：本博客中所采用的数据并非真实数据，会对真实数据加以变换，重在讨论游戏数据分析的思路。

这里是参考友盟的WAU模型[文章网址,  演示网址]，利用某款游戏（以下称为游戏A）数据进行的分析。

作用：

1. 根据转移矩阵，可以对未来的WAU进行预测；

2. 查看”WAU用户构成”可以发现游戏的问题：新增过少？流失过多？忠诚用户过少？

概念解释：

这里所说的第N周，是往前推的第N周，如下图所示：

1. 新增用户：注册时间在该周的用户。
2. 本周回流用户：上周未登录游戏，本周有登录游戏的用户。
3. 连续活跃N周的用户：在连续N周都有登录，但是在第N+1周没有登录，比如：连续3周，也就是往前推3周都有登录，但是往前的第4周没有登录。
4. 忠诚用户：连续5周及以上活跃的用户
5. 近期流失用户：连续n周（1<=n<=4）没有登录过游戏的用户（第n+1周启动过），比如：连续4周没有登录过游戏，但是第5周有启动过游戏。

根据上述定义，周活跃用户（WAU）由：新增用户、连续2周活跃用户、连续活跃3周、连续活跃4周、忠诚用户，组成。将每一种用户类型视为一种用户状态，各状态间的转移关系如下：

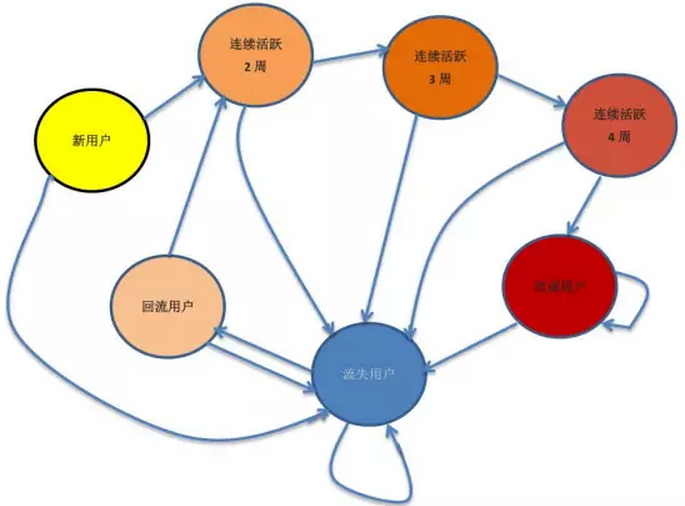
思路：

1.利用游戏A的活跃用户数据，按周将用户分成上述的各个类型，得到每周各个类型的人数；

2.计算前4周每周之间类型转移概率。得到3个转移概率矩阵，然后对矩阵中每项取平均值，得到如下的转移概率矩阵，用于后面WAU的预测。

注意到最后一行中：“近期流失用户”转换为“本周回流用户”和“近期流失用户”的概率之和不为1，这是前4周没有活跃且第5周有活跃的“近期流失用户”，在新的一周中，如果没有继续活跃，则不算是新的一周中的”近期流失用户“。

3.WAU预测

将前一周的各类型用户数乘以相应的转移概率，得到新一周的预测用户数。这里需要说明的是：新一周中“本周回流用户“是来自于两部分：1.上周的近期流失用户、2.上周的连续5周及以上没有登录的流失用户。对于第1部分的回流用户，直接用”上周的近期流失用户“乘以相应的转移概率即可。对于第2部分的回流用户如何计算呢？通过数据发现，（对于一款稳定的游戏而言）由”上周的近期流失用户“转化而来”回流用户“占总回流用户的比例是变化不大的，因此，计算"上周近期流失用户"转换而来的”本周回流“用户占比，前三周的值，取平均。然后用：近期流失用户*转移概率/该比值，即可得到预测的”本周回流用户“。预测的情况如下，与真实数据比较的误差率为3.6%

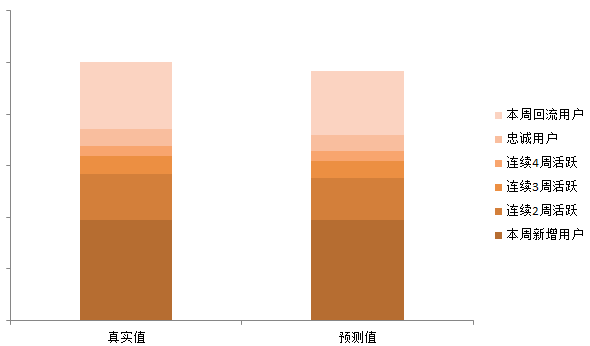
其他结论：

1) 由上面的转移矩阵可知：用户连续活跃的周数越多流失的概率也就越低，流失后再回流的概率相对也更高;

2) 由下面，各类型用户在WAU中的占比可以得出：新增用户在WAU中占比最多，而连续活跃2周以上的人数占比较少，说明游戏的用户主要来自于新增用户，而老用户的流失情况较为严重。因此，应主要关注新用户的转化率及老用户的留存流失情况。第二个方面，“回流用户”占比较多，但是“回流用户”转换为“连续2周活跃”的概率较小，说明有很多用户并不是频繁地登录游戏，间隔一周以上会玩一下，但是玩玩后有很快又会流失掉（7天没有登录游戏定义为流失），可以深入地去分析这部分回流用户，是否回流一次之后就再也不回来？如果是这种情况，则需要对这占比很大的“回流用户”采取挽留措施，比如，登录奖励、道具打折之类。还有一个原因，用户对游戏玩法已经感到疲劳，不愿再玩游戏，从而导致老用户的留存率很低，这就需要考虑是否增加新的场景或者角色或者道具来吸引用户。

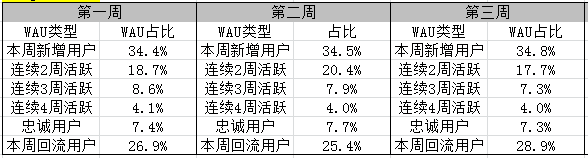
3) 忠诚用户的数量在这5周中整体呈下降趋势（此处没给出具体数据），这需要引起运营的注意，因为这些App最优质用户的流失是整个App活跃用户规模开始缩水的前兆。